В статье автор рассматривает малоизвестные и редко применяемые методы решения тригонометрических уравнений, основанные на знаниях геометрии, свойств функции, методов искусственных преобразований.
Ключевые слова: метод скалярного произведения, функционально-графический метод.
В современном мире тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как техника навигации, теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
В большинстве случаев решение тригонометрических уравнений сводится к двум стадиям: преобразование уравнения для получения его простейшего и его решение по формулам корней. Всем известны способы введения новой переменной, разложения на множители с использованием формул тригонометрии и других формул, метод решения однородных уравнений и др. В данной работе пойдет речь о нестандартных способах решения тригонометрических уравнений.
Функционально-графический метод
При изображении решений простейших тригонометрических неравенств иногда используют графики простейших тригонометрических функций. Для нахождения решения тригонометрического неравенства при этом подходе требуется схематичное построение графика простейшей тригонометрической функции и применение формул корней соответствующих уравнений.
Решить уравнение : sin x — 2x + 1 = 0.
Решение:
sin x = 2x — 1
Построим в одной системе координат графики функций y sin и y = 2x — 1.
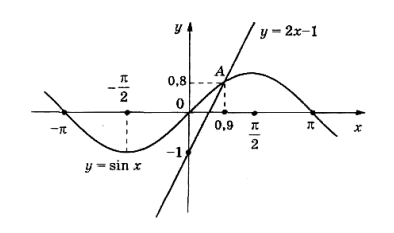
Графики функций пересекаются в точке A x 0.9; y 0.8.
Ответ: x = 0.9
Решение с исследованием функции
Область применения свойств функции при решении тригонометрических уравнений очень велика. Использование свойств (таких как ограниченность, монотонность и т. д.) функций, входящих в уравнение, также является нестандартным подходом, который мало кто использует. Их использование может облегчить решение нестандартных по формулировке задач. Но и не каждое уравнение в результате преобразований или при замене переменной может быть сведено к уравнению того или иного стандартного вида, для которого существует определенный алгоритм решения. В таких случаях на помощь также могут прийти свойства функций, содержащихся в уравнении. Предварительный анализ области допустимых значений неизвестной уравнения позволяет получить корни без преобразований уравнения.
Использование понятия области определения функции
Предварительный анализ области допустимых значений уравнения каких-то позволяет узнать корни, не производя преобразований уравнения.
Областью определения функции y = f(x) называется множество значений переменной х, при которых функция имеет смысл. Пусть дано уравнение f(x) = g(x), где f(x) и g(x) — элементарные функции, определенные на множествах D1, D2. Тогда областью D допустимых значений уравнения будет множество, состоящее из тех значений х, которые принадлежат обоим множествам, то есть D = D1 ∩ D2. Ясно, что когда множество D пустое (D = ∅), то уравнение решений не имеет.
Решить уравнение:
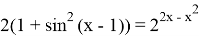
В одном равенстве присутствуют и тригонометрическая, и показательная функция, поэтому решить данное уравнение путем алгебраических преобразований невозможно.
Левая часть:
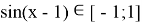
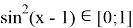
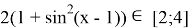
Правая часть:
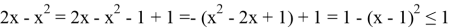
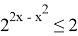
Получаем, что левая часть больше, либо равна двум, а правая меньше, либо равна двум. Тогда равенство выполняется, только когда обе части равны двум.
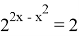
Ответ: x=1
Использование понятия области значений функции
Для использования ограниченности функции необходимо уметь находить множество значений функции и знать оценки области значений стандартных функций.
Областью значений функции y = f(x) называется множество значений переменной у при допустимых значениях переменной х. Функция y = f(x) называется ограниченной на данном промежутке (содержащемся в области ее определения), если существует такое число N > 0, что при всех значениях аргумента, принадлежащих данному промежутку, имеет место неравенство |f(x)| < N. Пусть дано уравнение f(x) = g(x), где f(x) и g(x) — элементарные функции, определенные на множествах D 1, D2. Обозначим область изменения этих функций соответственно E1 и E2. Если x1 является решением уравнения, то будет выполняться числовое равенство f(x1) = g(x1), где f(x1) — значение функции f(x) при x = x1, а g(x1) — значение функции g(x) при x= =x1. Значит, если уравнение имеет решение, то области значений функций f(x) и g(x) имеют общие элементы (E1 ∩ E2 ≠ ∅). Если же таких общих элементов множества E1 и E2 не содержат, то уравнение решений не имеет.
Отдельно выделю метод оценки.
Этот метод применяется при решении уравнений f (x) g(x), в которых его левые и правые части на всей ОДЗ удовлетворяют неравенствам f (x) M, g(x) M. В этом случае уравнение f (x) g(x) равносильно совокупности систем:
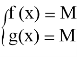
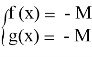
Соответственно, решив по отдельности каждое из уравнений приведенных систем, в дальнейшем нужно отобрать их общие решения.
Использование свойства монотонности функции
Функция f(x) называется возрастающей (убывающей) на числовом промежутке X, если большему значению аргумента x соответствует большее (меньшее) значение функции f(x), то есть для любых x1 и x2 из промежутка X таких, что x2 > x1, выполнено неравенство f(x2) > f(x1); f(x2) < f(x1).
Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
Ниже перечислено несколько свойств монотонных функций, используемых для установления характера монотонности функций и лежащих в основе утверждений об уравнениях и неравенствах.
Теорема 1 . Монотонная на промежутке X функция каждое свое значение принимает лишь при одном значении аргумента из этого промежутка.
Теорема 2 . Если функция f(x) возрастает (убывает) на промежутке X и функция g(x) возрастает (убывает) на промежутке X, то функция h(x) = f(x) + g(x) + C также возрастает (убывает) на промежутке X (С — произвольная постоянная).
Теорема 3 . Если функция f(x) неотрицательна и возрастает (убывает) на промежутке X, функция g(x) неотрицательна и возрастает (убывает) на промежутке X, C > 0, то функция h(x) = C*f(x)*g(x)также возрастает (убывает) на промежутке X.
Теорема 4 . Если функция f(x) возрастает (убывает) на промежутке X, то функция –f(x) убывает (возрастает) на этом промежутке.
Теорема 5 . Если функция f(x) монотонна на промежутке X и сохраняет на этом множестве знак, то функция 1/f(x) на промежутке X имеет противоположный характер монотонности.
Теорема 6. Если обе функции f(x) и g(x) возрастающие или обе убывающие, то функция h(x) = f(g(x)) — возрастающая функция. Если одна из функций возрастающая, а другая убывающая, то h(x) = f(g(x)) — убывающая функция. Сформулируем теоремы об уравнениях и неравенствах.
Теорема 7 . Если функция f(x) монотонна на промежутке X, то уравнение f(x) = C имеет на промежутке X не более одного корня.
Теорема 8. Если функция f(x) монотонна на промежутке X, то уравнение f(g(x)) = f(h(x)) равносильно на промежутке X уравнению g(x) = h(x).
Теорема 9. Если функция f(x) возрастает (убывает) на промежутке X, то неравенство f(g(x)) < f(h(x)) равносильно на промежутке X неравенству g(x) < h(x) (g(x) > h(x)).
Аналогичное свойство имеет место и для нестрогих неравенств.
Теорема 10. Если функция f(x) возрастает на промежутке X, а g(x) убывает на промежутке X, то уравнение f(x) = g(x) имеет на
промежутке X не более одного корня.
Теорема 11. Если функция f(x) возрастает на промежутке X, то уравнение f(f(x)) = x равносильно на промежутке X уравнению f(x) = x.
Монотонность функции на множестве R
Если функция f (t) строго возрастает на R, то f h(x) f g(x) равносильно уравнению h(x) g(x). Если функция f (t) строго убывает на R, то f h(x) f g(x) равносильно уравнению h(x) g(x).
Монотонность функции на промежутке
Если функция f (t) строго монотонна на своей области существования — промежутке м, то уравнение f h(x) f g(x) равносильно системе:
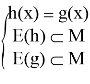
Функции разной монотонности
Уравнение u(x) v(x), где u(x) — возрастающая, а v(x) — убывающая функции, либо не имеет решений (а), либо имеет единственное решение (б).
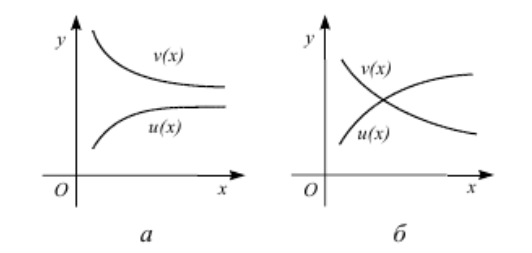
Использование свойств четности или нечетности функций
Функция f(x) называется четной, если для любого значения x, взятого из области определения функции, значение –x также при-
надлежит области определения и выполняется равенство f(–x) = f(x).
Функция f(x) называется нечетной, если для любого значения x, взятого из области определения функции, значение –x также принадлежит области определения и выполняется равенство f(–x) = –f(x).
Из определений следует, что области определения четной и нечетной функций симметричны относительно нуля (необходимое условие).
Для любых двух симметричных значений аргумента из области определения четная функция принимает равные числовые значения, а нечетная — равные по абсолютной величине, но противоположного знака.
Теорема 1. Сумма, разность, произведение и частное двух четных функций являются четными функциями.
Теорема 2. Произведение и частное двух нечетных функций представляют собой четные функции. Пусть имеем уравнение или неравенство F(x) = 0,
F(x) > 0 (F(x) < 0), где F(x) — четная или нечетная функция.
а) Чтобы решить уравнение F(x) = 0, где F(x) — четная или нечетная функция, достаточно найти положительные (или отрицательные) корни, после чего записываются отрицательные (или положительные) корни, симметричные полученным, и для нечетной функции корнем будет x = 0, если это значение входит в область определения F(x). Для четной функции значение x = 0 проверяется непосредственной подстановкой в уравнение.
б) Чтобы решить неравенство F(x) > 0 (F(x) < 0), где F(x) — четная функция, достаточно найти его решения для x<0 (или x>0).
Действительно, если решением данного неравенства является промежуток
(x1; x2), где x1, x2 — числа одного знака или одно из них равно нулю, то его решением будет и промежуток (–x2; –x1).
в) Чтобы решить неравенство F(x) > 0 (F(x) < 0), где F(x) — нечетная функция, достаточно найти решения для x > 0 (или x < 0).
Если нам известны промежутки знакопостоянства функции F(x) для x > 0 (или x < 0), то легко записать промежутки знакопостоянства и для x < 0 (или x > 0).
Использование свойства периодичности функции
Функция y = f(x) называется периодической, если существует такое число T? 0, что для любого значения x, взятого из области определения, значения x + T, x — T, также принадлежат области определения и выполняется равенство f(x) = f(x + T) = f(x — T). Число T называется периодом функции. Всякая периодическая функция имеет бесконечное количество периодов. При решении уравнений и неравенств будем использовать наименьший положительный период функции.
Если функция F(x) — периодическая, то решение уравнения F(x) = 0 или неравенства F(x) > 0 (F(x) < 0) достаточно найти на промежутке, равном по длине периоду функции, после чего записывается общее решение. Если периодическая функция еще и четная или нечетная, то решение достаточно найти на промежутке, равном по длине половине периода.
Методы искусственных преобразований
В некоторых случаях при решении нестандартных тригонометрических уравнений не представляется возможным использовать вышеперечисленные методы, либо такие пути решения не рациональны. Для их решения необходимо воспользоваться методами искусственных преобразований:
– Умножение обеих частей уравнения на одну и ту же тригонометрическую функцию
– Прибавление к обеим частям уравнения одного и того же числа, тригонометрической функции
– Тождественные преобразования одной из частей уравнения (прибавление и вычитание одного и того же выражения)
– Использование свойств пропорции:
При a/b = c/d:
– (a+b)/(a-b) = (c+d)/(c-d)
– (a-b)/(a+b) = (c-d)/(c+d)
– (a-c)/(b-d) = a/b
– (a+c)/(b+d) = a/b
При использовании данного метода необходимо помнить, что применение приведенных выше преобразований может привести к появлению новых корней у уравнения. Для избегания таких ошибок можно умножать/прибавлять/вычитать/делить только на уравнения, не имеющие корней или обязательно проводить в конце решения проверку всех корней, подставляя их в исходной уравнение.
Решить уравнение:
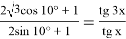
D(y):
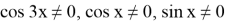
По свойству пропорции: при a/b = c/d выполняется (a+b)/(a-b) = (c+d)/(c-d), тогда:
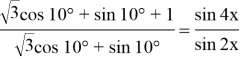
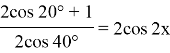
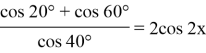
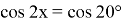
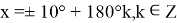
Расширения области допустимых значений не произошло.
Ответ:
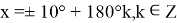
Геометрический метод при отборе корней (Метод скалярного произведения векторов)
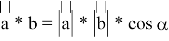
Так как |
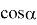
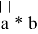

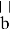
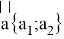
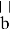
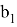
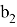
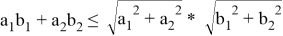
Решить уравнение:
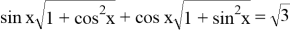
Введем векторы
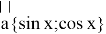
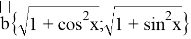
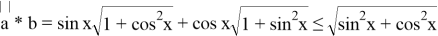
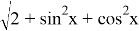
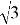
Таким образом получаем
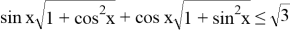
Очевидно, что исходное уравнение можно записать в виде
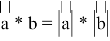
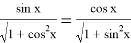
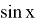
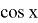
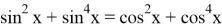
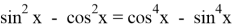
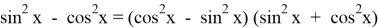
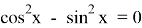
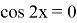
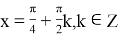
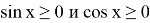
Ясно, что
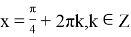
Ответ:
Тригонометрия не является прикладной наукой, поэтому в повседневной жизни она редко применяется. Однако это не уменьшает ее значимость. Тригонометрию применяют в астрономии, навигации, оптике, теории музыки, акустике, электронике, анализе финансовых рынков, теории вероятностей и статистике, биологии и медицине (в расшифровке ультразвуковых исследова-ний УЗИ и компьютерной томографии),теории чисел, метеорологии, химии, сейсмологии, фармацевтике, химии, океанологии, многих разделах физики, картографии, топографии, геодезии, архитектуре, электронной технике, фонетике, экономике, компьютерной графике, машиностроении и т. д. И, скорее всего, в будущем область ее применения будет становиться все более обширнее. В ходе выполнения исследовательской работы изучены различные нетрадиционные методы решения тригонометрических уравнений, помимо тех, которые изучаются в школе, обобщен и систематизирован изученный материал. Важно отметить, что все представленные выше методы решения удобны для решения тригонометрических уравнений, но каждый из них имеет свои особенности, положительные и отрицательные стороны. Для некоторых уравнений данные методы являются единственным возможным вариантов решения, а для других — более рациональным и простым.










