В статье автор рассказывает о наиболее часто встречающихся куполах православных церквей и описывает механизм его построения.
Ключевые слова: окружность, луковичный купол, золотое сечение
Храмы с древнейших времен составляли неотъемлемую часть панорамы города. Как невозможно себе представить Афины без Парфенона или древний Рим без Капитолия, так трудно было бы вообразить Париж без Нотр-Дам, Лондон без Вестминстерского аббатства, а Москву без кремлевских соборов. Храм в городе — это пророк, говорящий о вечности, чей зов раздается среди шума современной цивилизации.
Протоиерей Александр Мень
Россия возвращается к своим истокам и культурным традициям. Мы стараемся больше узнавать о нравственных и духовных ценностях, накопленных поколениями людей, об их взглядах на мир. В последние два десятилетия в Калининграде были построены и реконструированы православные храмы. Каждый храм особенный и ему трудно найти подобный. В своей неповторимости заключен определенный символ. Проблема символики христианской архитектуры является актуальной, потому что в христианской церкви все имеет две природы — духовную и материальную. Материальное непосредственно доступно нашему восприятию, на духовное указывает символика. Поэтому любому человеку необходимо иметь о ней представление, чтобы владеть историей и культурой своего народа.
Самой важной частью любого храма является купол, который несёт в себе разную символику. Поэтому цель нашей работы — выявить архитектурную символику куполов православных храмов города Калининграда, расследовать различные виды куполов и математические способы их построения.
Гипотеза — воснове современного строения куполов лежат традиции и символика русского христианского храма. Основной фигурой для построения куполов является окружность, купола соборов, имеющие «луковичную» форму, построены по принципу золотого сечения, с соблюдением канонов архитектуры крестово-купольных храмов.
Практическое применение. Материалы данной работы можно использовать в качестве дополнительной литературы на уроках исторического и литературного краеведения, МХК, изобразительного искусства, во внеклассной работе, а также на уроках геометрии при изучении радиуса, диаметра окружности.
История появления куполов.
Купол (итал. Cupola — купола, свод, от лат. cupula, уменьшительное от cupa — бочка) — пространственная, несущая конструкция покрытия, по форме близкая к полусфере или другой поверхности вращения кривой [2].
Главное в храме — купола. К ним особое внимание и отношение. Купол может быть разной формы, цвета, и имеет разное количество глав. Все характеристики имеют свое символическое значение.
История куполов началась еще в доисторические времена. Купола стали строить во время римской архитектурной революции, когда их стали использовать при строительстве храмов и больших общественных сооружений. Считается, что самый древний купол, из ныне существующих, расположен в римском Пантеоне, возведенном примерно в 128 году нашей эры. Позже традиция куполостроения была перенята византийской религиозной и культовой архитектурой.
Византийская империя подарила Руси умение строить храмы и возводить купола. Русское искусство, начиная с Х в. и вплоть до конца ХV11 столетия неразрывно связано с Церковью и христианской верой. Первым городом на Руси, принявшим крещение, стал Киев. Богослужение в великом православном храме Византии — храме Святой Софии города Константинополя повлияло на послов князя Киевского Владимира.«Не знаем, на небе ли были мы или на земле, ибо нет на земле такого вида и такой красоты…»
Именно это переживание красоты как святости было положено в основу нового искусства на русской земле. Византийскими мастерами было возведено много храмов в традициях византийского зодчества.
Храмы Калининграда
Особенность Калининградской области связана с уникальной историей региона, который до 1945 года был частью Германии, а затем, в 1946 году, по решению Потсдамского соглашения, вошёл в состав РСФСР. Эта особая специфика выражается так же в обилии нехарактерных для России лютеранских храмов (кирх). До 1985 года в Калининграде не было ни одного православного храма. Экскурсоводы сообщали, что Калининград до недавнего времени имел репутацию самого «безбожного» города.
Бурная религиозная жизнь в регионе началась с 1992 года, после распада СССР.
6 октября 1985 года православные освятили первый приход в помещении бывшей немецкой Юдиттен-кирхи — Свято-Никольский храм Русской православной церкви (рис.1).

Рис. 1. Свято-Никольский храм Русской православной церкви
Православная община первоначально входила в состав Смоленской и Вяземской епархии. В 1988 году было учреждено Калининградское благочиние. Рост православия в Калининграде привёл к переименованию епархии, которая в 1989 году стала называться «Смоленской и Калининградской епархией». 10 сентября 2006 года Патриархом Московским и всея Руси Алексием II в Калининграде был освящён новый православный Храм Христа Спасителя Русской православной церкви (рис. 2).

Рис. 2. Храм Христа Спасителя Русской православной церкви
31 марта 2009 года была образована отдельная Калининградская епархия, выделенная из Смоленско-Калининградской епархии. Она насчитывает 168 храмов и 38 часовен. Часть православных церквей располагаются в зданиях бывших лютеранских храмов (например, Кирха Понарт) [5].
Классификация куполов церквей Калининградской области
|
Название храма, год постройки/адрес |
Форма купола |
Кол-во куполов |
Цвет куполов православных храмов |
|
Свято-Елисаветинский монастырь, 2001/пос.Приозерье, Калининградской области |
Луковичная |
1 |
золотое покрытие |
|
Храм Христа Спасителя, 2006/площадь Победы, Калининград |
Шлемовидная |
5 |
золотое покрытие |
|
Храм Кирилла и Мефодия, 2020/проспект Мира, 123-б |
Луковичная |
7 |
золотое покрытие |
|
Храм Святого Александра Невского, 2014/ул.А.Невского |
Шатровая |
5 |
Изголовье золотое покрытие |
|
Храм Андрея Первозванного |
Шлемовидная |
1 |
золотое покрытие |
|
Храм Илии Муромца при КПИ ФСБ России, 2011/ул. Подполковника Емельянова, 244, Калининград |
Луковичная |
1 |
золотое покрытие |
|
Храм прав. воина Феодора Ушакова при Балтийском военно-морском институте /Калининград, Советский пр-т 82 |
Луковичная |
1 |
голубое |
|
Храм Святых Петра и Февроньи, 2011/Площадь Победы, Калининград |
Шлемовидная |
2 |
золотое покрытие |
|
Храм Тихвинской иконы Божией Матери г. Пионерский |
Луковичная |
1 |
золотое покрытие |
|
Никольская церковь — Церковь Николая Чудотворца в морском порту, 2013 |
Шатровая |
1 |
золотое покрытие |
Из представленных в таблице сведений видно, что большинство храмов Калининградской области имеет луковичную форму (50 %), поэтому проведем геометрическое построение эскиза «луковичного» купола.
Исследование геометрического построения эскиза «луковичного» купола. Построение купола «луковичной» формы
Исследуем различные построения эскиза «луковичного» купола. Проследим, какие закономерности положены в его основу.
Золотым сечением (делением), «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей. Это отношение приближенно равно 0,618 или 5/8.
Задача 1. Построение купола-луковица
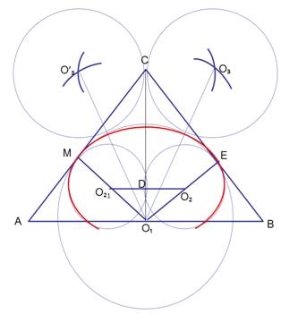
- Провести перпендикуляр СО1 к АВ;
- Провести перпендикуляры О1Е к СВ и О1М к АС;
- Из точки О1 провести окружность, с радиусом О1Е;
- Отложить СД = О1В;
- Через точку Д провести прямую, параллельную АВ и получить точки О2 и О21;
- Провести окружности из центров О2 и О21 одинакового радиуса равного О2Е;
- Вырисовывается нижняя часть купола;
- Точки О3 и О31 получить пересечением окружности с центром О1 и радиусом 2О1Е, а также окружности с центром С и радиусом равным О1Е;
- Из точек О3 и О31 провести такие же окружности;
- Линия, составленная из двух построенных дуг, образует верхнюю часть эскиза купола;
- От точки О1 на АВ отложить по обе стороны отрезки, равные ¼ АВ и провести прямые, перпендикулярные АВ, получаем нижнюю часть эскиза купола. (28–30 сл.)
Инструкция для построения луковичного купола
Прежде всего выберем единицу измерения — отрезок е = 3 см.
Затем выполним преобразования MN: HO = 1,6 = 16: 10 = 8: 5. Это значит, что MN = 8е = 24 см, а HO = 5е = 15см. Представим себе, что нам следует построить равнобедренный треугольник MNH, у которого основание MN и высота HO составляют золотую пропорцию.
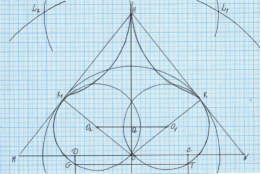
- Провести перпендикуляр HO к MN.
- Провести перпендикуляры OK к HN и OK 1 к MH.
- Из точки О провести окружность с радиусом ОK.
- Отложить HQ = ОN.
- Через точку Q провести прямую, параллельную MN и получить точки О 1 и О 2 .
- Провести окружности из центров О 1 и О 2 одинакового радиуса, равного О 1 K.
- Точки L 1 и L 2 получить пересечением окружности с центром О и радиусом 2ОK, а также окружности с центром H и радиусом, равным ОK.
- Из точек L 1 и L 2 провести такие же окружности радиусом, равным ОK.
- От точки О на MN отложить по обе стороны отрезки, равные MN и через концы отрезков C и D провести прямые, перпендикулярные MN, до пересечения с окружностями, проведенными из точек О 1 и О 2 радиусами О 1 K.
- Линия, составленная из двух построенных дуг TK и KH, MK 1 и K 1 H образует эскиз купола.
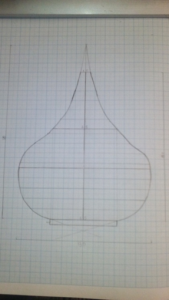
Получили вот такой вид «луковичного» купола:
Заключение
Так, в Калининграде к памятникам архитектуры, построенным по золотой пропорции, относятся Храм Тихвинской иконы Божией Матери г. Пионерский, Храм прав. воина Феодора Ушакова при Балтийском военно-морском институте, Храм Илии Муромца при КПИ ФСБ России, Храм Кирилла и Мефодия и многие другие. Проведя некоторые исследования и вычисления, можно убедиться, что все купола, имеющие «луковичную» форму, построены по принципу «золотого сечения», видно, что построение полностью совпадает с геометрическими раскладками золотого сечения.
Если в основе построения купола лежит равнобедренный треугольник, стороны которого составляют числа, выражающие золотую пропорцию, то храм построен по закону «золотого сечения».
Таким образом, купола соборов в Калининграде и области, имеющие «луковичную» форму, построены по принципу золотого сечения, с соблюдением канонов архитектуры крестово-купольных храмов. Выдвинутая гипотеза нашла свое подтверждение в ходе проведенного исследования.
В работе исследованы закономерности построения эскиза «луковичного» купола, выполнен эскиз «луковичного» купола с помощью циркуля и линейки, где понадобились знания из геометрии по темам «Задачи на построение», «Золотое сечение», «Симметрия», и по данному эскизу построен купол «луковичной формы».
Таким образом, используя геометрические знания, знания истории, архитектуры, можно построить купол «луковичной» формы.
Литература:
- Стародубцев О. Символика православного храма [электрон. ресурс]. — Режим доступа: http://www.pravoslavie.ru/jurnal/061214101726.htm
- Еремина Т. С. Русский православный храм. История. Символика. Предания. — М.: Прогресс-Традиция, 2002.
- Галанин А. В. Купола и главы храмов. — М: прогресс-Традиция, 2010г.
- Народный каталог православной архитектуры // http://sobory.ru
- Гуров И. Д., консультант комитета по информации, печати и связям с общественностью администрации Калининградской области. «Балтийский альманах». Конфессии в Калининграде. Официальный сайт администрации городского округа «Город Калининград» // klgd.ru

