Квадрат длины медианы в произвольном треугольнике



В данной статье рассматривается вывод формулы длины медианы в произвольном треугольнике. Вывод формулы разными способами даёт возможность учащимся повторить широкий спектр геометрических фактов, совершенствовать навыки применения разных методов и приёмов решения задач, способствует более глубокому и прочному пониманию и запоминанию материала.

Ключевые слова: медиана, длина, полупериметр, произвольный треугольник.

Математика — это искусство называть разные вещи одним и тем же именем.

А. Пуанкаре

Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны (рис. 1). Медиана, соединяющая вершину A треугольника с серединой стороны a , обозначается m _a .

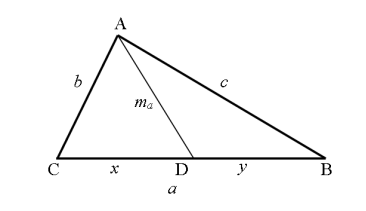
Рис. 1

На сегодня известны две формулы квадрата длины медианы в произвольном треугольнике:

1. Через стороны треугольника:

, (1).

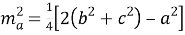
где a, b, c — стороны треугольника, x , y — отрезки основания медианы, A, B, C — углы треугольника.

Докажем эту формулу, для чего воспользуемся теоремой Стюарта: Если точка D лежит на стороне BC треугольника АВС (рис.1), то имеет место следующее равенство:

или , тогда, учитывая, что , будем иметь: , что и требовалось доказать.

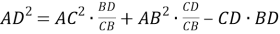
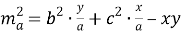
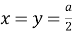
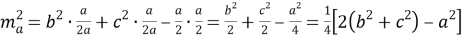
Задача. В треугольнике АВС (рис.1) проведена медиана АD . Известно, что b=8 , c=10 и m _a =7. Найти a .

2. Через две стороны и угол: , (2).

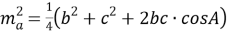
Докажем эту формулу, для чего рассмотрим треугольник АВС (рис.1) со сторонами a, b и c . Из вершины А на сторону СВ=a опустим медиану АD=m _a . Из треугольника АВС по теореме косинусов, имеем: . С другой стороны воспользуемся выражением (1): Используя эти два выражения, получим: , отсюда или , что и требовалось доказать.

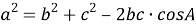
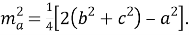
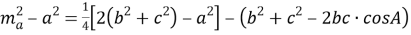
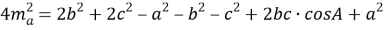
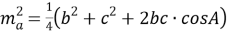
Задача. В треугольнике АВС (рис.1) проведена медиана АD . Известно, что b=8 , c=10 и m _a =7. Найти угол А .

Рассмотрим зависимость квадрата длины медианы в произвольном треугольнике через полупериметр и стороны.

Используя формулу двойного угла

с учётом, что и , будем иметь: , отсюда , (3). Из треугольника АВС по теореме косинусов имеем: , отсюда , (4). Используя выражения (3) и (4), получим: , отсюда , (5). Используя выражения (1) и (5), будем иметь: , отсюда , (6).

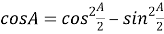
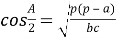
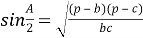
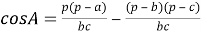
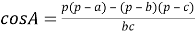
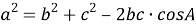
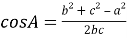
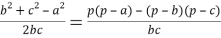
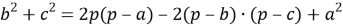
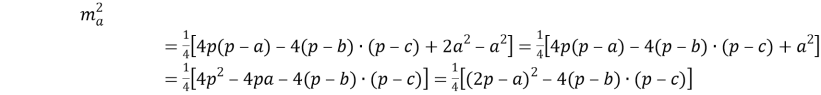
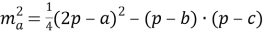
Таким образом, квадрат длины медианы произвольного треугольника равен одной четвёртой квадрата разности периметра и одной из сторон треугольника без произведения разностей полупериметра и каждой из двух других его сторон.

Задача. В треугольнике АВС (рис.1) с полупериметром 21см и сторонами b=14см и c=12см из вершины А проведена медиана m _a . Найти квадрат медианы.

Литература:

1. Выгодский М. Я. Справочник по элементарной математике. Москва. «Наука». 1986.
2. Некрасов В. Б. Школьная математика. Санкт-Петербург. «Авалон». 2006.