Девятое задание тестовой части ЕГЭ по профильной математике



Статья посвящена новому заданию тестовой части ЕГЭ по профильной математике. В статье указаны несколько способов решения этого задания. Содержание статьи будет полезным преподавателям и студентам.

Ключевые слова : задача, парабола, решение, дополнительная система координат, способ решения, уравнение параболы.

В 2022 году в демоверсии ЕГЭ была представлена новая задача под номером девять. Она не сложна, но при этом может отнять немало времени на решение. Рассмотрим несколько методов решение этой задачи и найти самый быстрый из них.

Условие задачи. На рисунке изображён график функции вид где числа a, b и c — целые. Найдите значение .

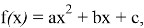
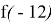
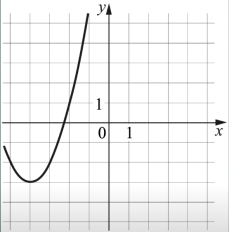
Как же это решать? Ну, если пойти самым очевидным и простым методом, то внимательно посмотрев на график, необходимо выбрать три любые целочисленные точки. Допустим это будут точки: . Теперь просто подставим значения

и в исходное уравнение функции. Получаем систему из трёх линейных уравнений:

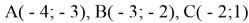
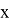
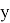
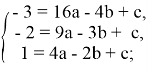
И теперь задача сводится к нахождению a, b и c. Есть три уравнения и три неизвестные. Начнём с ними работать. Вычтем последнее уравнение из первых двух. Тогда получаем:

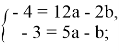
Заметим, что верхнее уравнение можно сократить на 2. В итоге у нас получается:

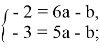
Дальше остаётся только вычесть из верхнего уравнения нижнее, после чего получаем значение a:

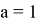
Ну и теперь подставляем это значение в любое из уравнений получаем что:

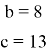
Теперь, зная все коэффициенты функции и понимая, что изначальная функция выглядит так, запишем уравнение исходной параболы:

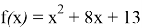
Зная это, уже вполне окончательно можно решить задачу:

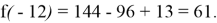
Данный способ решения самый простой и не вызывает трудностей в решении. Но на самом деле, если чуть-чуть подумать, можно сильно сократить рассуждения, даже в этом решении. Вспомним как устроена парабола около её вершины. Построим дополнительную систему координат, началом отсчёта которой будет являться вершина этой параболы. Тогда можно заметить, что это парабола вида но с небольшим сдвигом. Понимая, что при движении параболы её старший коэффициент не меняется, то получаем значение . И всё решение по -итогу сводится к решению системы линейных уравнений, но уже с двумя неизвестными. Решение будет схожим, но только быстрее, ведь пропускается одно из преобразований.

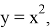
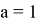
Вторым шагом, способным упростить решение, является понимание, что вершина любой параболы находится в точке :

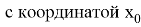
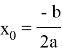
Уже зная, что получим:

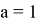
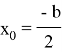
Но, посмотрев на график, становится понятно, что . Тогда:

;

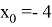
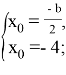
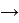
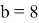
А зная значение , для решения нам потребуется всего лишь одно уравнение, подставив полученные значения в которое, находим значение .

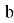
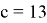
Эти методы решения связаны с понимаем того, как ведёт себя парабола при её движении по координатной плоскости.

Но существует ещё более быстрый способ решения. Для этого необходимо знать, как ведёт себя уравнение параболы при её сдвиге. Если изначально была парабола

, то чтобы получит график параболы, показанный на рисунке, эту параболы необходимо сдвинуть на 4 влево и на 3 вниз. То есть уравнение необходимой нам параболы принимает форму:

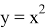
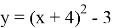
Получилось, что при понимании того, как меняется уравнение параболы при её движении, можно без дополнительных точек решить данную задачу:

.

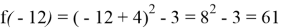
Но существует, самый быстрый способ решения данной задачи. Если вспомнить, что уже есть дополнительная система координат, понимаем, что парабола в этой новой системе будет вести себя также, как и парабола вида в изначальной. Если вернуться к условию и понять, что спрашивают, какое значение примет функция при , то, рассмотрев эту задачу в новой системе координат, то понимаем, что на самом деле необходимо найти значение функции при , ведь график смещён на 4 влево. Но необходимо помнить, что парабола также смещена ещё и на 3 вниз, следовательно задача обретает вид:

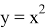
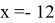
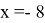
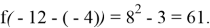
Это решение будет самым быстрым, но не самым лёгким. Первый способ решения подходит для любой новой задачи под номером 9, но чтобы решать её быстрее, необходимо глубже понимать геометрию разных графиков функций. Поэтому данная задача и хороша, ведь способ и скорость её решения зависит исключительно от набора знаний ученика, и только от него зависит, сколько времени он на неё потратит.