
Что мы знаем о пауках? Мы их боимся, они нам неприятны. А что такое паутина? Этому вопросу была посвящена исследовательская работа «Обыкновенные пауки и их необыкновенная паутина» в прошлом году, но изучая свойства паутины, наблюдая за пауками, у меня возник вопрос: а существуют ли геометрические фигуры в природе? Является ли паутина геометрической фигурой?
350 миллионов лет назад суша Земли была безжизненна. Именно тогда на сушу вышли предки скорпионов и пауков. Миллионы лет им пришлось приспосабливаться к новому дому, погибая и выживая целыми колониями. Мух тогда еще не было, они появились на Земле намного позже. Есть предположение, что в те времена мухи не летали и научились они летать, благодаря паукам. И тогда, чтобы ловить уже крылатых насекомых, пауки научились плести свои сети.
Эволюция пауков — это эволюция их паутины. Круговая сеть пауков очень необычна и не проста. Паук, плетя ее, применяет особые материалы, особые методы плетения. Когда наблюдаешь за его работой, кажется, что все его действия продуманны до особых деталей, рассчитаны будто математически! Очень изящную сеть строит паук крестовик, верней паучиха. Вот это математика! Углы между всеми радиусами и расстояния между всеми паучьими спиралями строго постоянны, даже если предположить, что чертежи и проект конструкции заложены у паука генетически, все равно для сверки углов нужен хотя бы простейший измерительный прибор. Наблюдая за этим, биологи утверждают, что все дело в первой паре ног мохнатого строителя. Именно эти ноги выполняют функцию масштабной линейки. Именно ими паук измеряет расстояние между спиралями.
Я все лето наблюдал, как паук крестовик плетет свою паутину. Ветер и дождь ломали ее, но паук снова и снова плел ее вечером, восстанавливая все спирали и радиусы. Именно так я их называл, глядя на паутину. И если это действительно спирали, действительно радиусы, то паутина — это окружность?
Окружность. Начало
Рассмотрим, что же такое окружность. Как она появилась в мире людей. Уже понятно, что человек взял окружность из природы, может быть даже, глядя на паутину.
От Аравийского полуострова, текут две большие реки — Евфрат и Тигр. Между ними длинная узка полоса земли. Когда-то давно, в древности, её называли Месопотамией, в переводе — «Междуречье». Самым известным государством Месопотамии был Вавилон.

Вавилоняне были земледельцами. Им приходилось очень трудно, т. к. Евфрат и Тигр разливались очень бурно. Защищаясь от наводнений, людям приходилось строить дамбы, обносить селения и поля насыпями. Для строительства таких сооружений нужны знания, поэтому в Вавилоне начала развиваться математика. И вот, шесть тысяч лет назад, в Вавилоне было сделано великое открытие: ученые изобрели колесо.
Благодаря этому открытию Вавилонские воины ездили на боевых колесницах и легко побеждали пеших врагов. Вавилонские инженеры изобрели кран, благодаря которому поднимали тяжелые грузы. Колесо и рычаг были самыми лучшими помощниками людей при работе с тяжестями. Был изобретен гончарный круг, стали изготавливать круглую посуду. Изобретение колеса стало важным этапом в развитии Вавилона и всего человечества, а вавилонские ученые продолжали изучение свойств окружности.
Прежде всего, ученые начали измерять длину окружности. Оказалось, это сложно, ведь линейкой замерить длину не получалось. Вот как изначально измерялась длина окружности: чертили окружность, внутри ее чертился квадрат, так, чтобы его углы упирались в окружность. Второй квадрат чертили снаружи окружности, так, чтобы он был надет на окружность и упирался в нее серединами сторон. Затем измеряли длину сторон большого квадрата и длину сторон меньшего квадрата, получившиеся числа складывали и затем делили пополам. Считали, что это и была длина окружности. Результат получался в три раза больше, чем диаметр. Это не самый точный способ измерения, но в те времена такого результата было достаточно.
Если нужно было получить более точный результат, то вместо квадратов рисовали шестиугольники или двенадцатиугольники. Стороны многоугольника ближе к окружности, а, следовательно, и результат получался более точный. В вавилонских задачах отношение длины окружности к длине диаметра почти совпадает с тем числом, которым мы пользуемся для вычислений в наше время.
Вычисление длины окружности
Окружностью называется множество точек плоскости, находящихся на одном расстоянии от данной точки (центра окружности).
Начертим окружность, с центром в точке О. Поставим точку М на окружности. Отрезок ОМ является радиусом (R) окружности.
Отрезок, который соединяет две точки окружности, называется хордой. Хорда, которая проходит через центр окружности, называется диаметр (D).
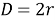
Длиной окружности называется длина замкнутой кривой, которая ограничивает круг. Формула длины окружности (С):
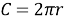
Концентрические окружности.
Концентрические окружности — окружности разного радиуса, описанные из одного центра. Концентрический — имеющий общий с другим центр, но неодинаковые размеры, например, концентрические круги, имеют общий центр, но разные радиусы, так что один лежит внутри другого.
Я решил проверить, насколько расчеты вавилонцев были верны. Начертил три окружности с равным диаметром.
Длину первой окружности я замерял с помощью двух квадратов, описанного и вписанного в окружность. Длину второй окружности я замерял с помощью двух шестиугольников.
И длину третьей окружности замерил с помощью формулы.
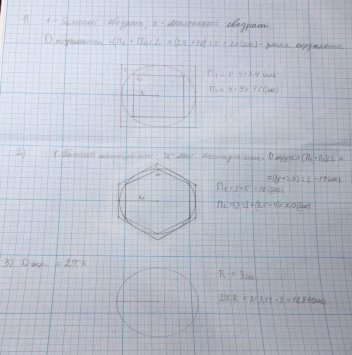
Вывод: Вавилонцы оказались правы.
Наблюдая за пауком, я перенес все размеры паутины на макет.

Затем сделал ее замеры. Длина синей нити составила 60 см, длина классной нити 73 см. Длина всей «паутины» составляет
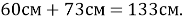
Теперь вычислим длину паутины с помощью математических формул. Для этого сделаем математическую модель паутины в виде четырех концентрических окружностей и найдем длину этой «паутины»
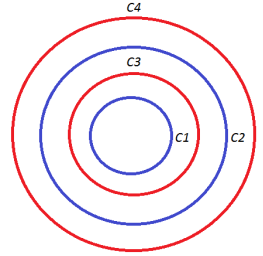
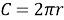
1) Радиус первой синей линии приблизительно 2,5 см, радиус второй синей линии равен приблизительно 5 см.
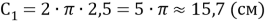
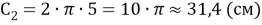
Длина всей синей линии
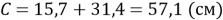
2) Радиус первой красной линии приблизительно 5 см, радиус второй красной линии равен приблизительно 7 см.
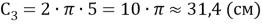
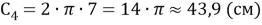
Длина всей синей линии
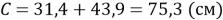
Длина всей «паутины»:
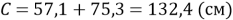
Теперь сравним длину «паутины» полученную практическим и арифметическим способом.
Синяя нить и синяя линия:
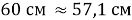
Красная нить и красная линия:
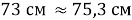
Длина всей «паутины»:
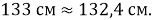
Очевидно, что арифметический и практический способы измерения «паутины» имеют небольшое расхождение, погрешность невелика.
У меня получилось измерить длину паутины, создать математическую формулу для измерения длины паутины, проверить практическим путем формулу длины окружности и формулу длины паутины.
Моя гипотеза нашла подтверждение. Действительно, паутина представляет собой концентрические окружности, длины которых можно найти с помощью формулы длины окружности.
Я считаю, что необходимо как можно больше читать научной литературы, изучать природу и проводить собственные исследования, которые, возможно, приведут к новым открытиям и принесут пользу человечеству.
Литература:
- Акимушкин И. И. Мир животных. Насекомые. Пауки. Домашние животные / И. И. Акимушкин. — Москва: Мысль, 1990. — 462 с.: ил.
- Богоявленская О. Б. Беспозвоночные животные / О. Б. Богоявленская, Е. Ю. Лобанов, Е. В. Коророва. — Екатеринбург: Банк культурной информации, 1994. — 112 с.: ил.
- Вартбург М. Пауки и паутины / М. Вартбург // Знание — сила. — 2007. — № 8. — С. 44–46.
- Депман И. Я. Мир чисел: рассказы о математике / И. Я. Депман; рис. Ю. Киселёва. — Изд. 4-е, перераб. и доп. — Ленинград: Детская литература, 1982. — 71 с.: ил. — (Библиотечная серия.)
- Кордемский Б. А. Удивительный мир чисел и фигур. Задачи, загадки, головоломки, ребусы и игры с математическим содержанием / Б. А. Кордемский. — Москва: Издательство АСТ: Мир и Образование, 2019. — 352 с.: ил. — (Интеллектуальные игры и головоломки).
- Лапшина И. Целительная паутина и немного о ее создателях / И. Лапшина // Природа и человек (Свет). — 2006. — № 11. — С. 26–27.
- Манкевич Р. История математики / Ричард Манкевич; [перевод с англ. А. Степановой]. — Москва: Ломоносовъ, 2011. — 256 с.

