На сегодняшний день по всему миру найдутся тысячи энтузиастов, которые уверены в том, что будущее нужно строить уже сейчас. Ричард Обузи — один из основателей и президент компании Icarus Interstellar, отмечает: «Межзвездные перелеты — это международная инициатива многих поколений людей, которая требует огромных интеллектуальных и финансовых затрат. Уже в наши дни мы должны инициировать необходимые программы, для того чтобы через сотню лет человечество смогло вырваться за пределы нашей Солнечной системы» [5].
Принимая во внимание беспрецедентную сложность и грандиозность межзвездной экспедиции, ее нельзя рассматривать как самостоятельную научно-техническую задачу. Это долгосрочная, многоэтапная и комплексная программа, которая будет определять стратегию всей космической деятельности человечества. Разработка межзвездного корабля любого типа, вне зависимости от заложенных в его конструкцию физических принципов движения, должна начинаться с компьютерного моделирования.
Таким образом, актуальной является задача компьютерного моделирования межзвездных полетов и разработка на этой основе конструкций, позволяющих осуществить межзвездное путешествие.
К достоинствам компьютерного моделирования межзвездных полетов следует отнести:
– быструю настройку модели на новый объект изучаемого класса и возможность анализа разнообразных физических эффектов;
– возможность оптимизации параметров межзвездного полета.
В настоящее время при моделировании сложных технических систем широкое распространение получают технологии визуального компьютерного моделирования. Применение этих технологий в сочетании с адекватными математическими моделями позволяет исследовать изучаемые процессы в режиме виртуальной реальности, что имеет особое значение, если мы имеем дело с процессами, протекающими в межзвездном пространстве, где надежная регистрация отдельных параметров в ходе натурного эксперимента на данном этапе невозможна.
Целью исследования — создание компьютерной модели межзвездных полетов на языке программирования PascalABC.NET.
Сложность рассмотрения перелета от Солнца к другим звездам с использованием корректировки движения летательного аппарата была связана с подбором адекватной физической модели и математического аппарата.
В процессе подбора математического аппарата для описания движения тел мы остановились на методе Эйлера, как наиболее простом численном методе решения (систем) обыкновенных дифференциальных уравнений. Данный метод был описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление» [6]. Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно-линейной функцией — ломаной Эйлера.
При составлении модели необходимо учесть, что в нашей системе известны скорости изменения переменных х 1 , х 2 ,…. х N в некоторый момент времени t 0 , и хотим узнать значения в другой момент t > t 0
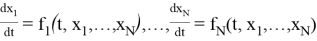
В обыкновенных дифференциальных уравнениях все переменные х 1 , х 2 ,…. х N являются функциями одной независимой переменной t . Мы будем рассматривать уравнения только с первыми производными по времени (первого порядка), так как уравнение n-го порядка можно свести к системе n уравнений первого порядка.
Обозначим набор наших переменных х 1 , х 2 ,…. х N через X , а набор функций f 1 ,.., f N через F , тогда систему уравнений можно записать в символическом виде:
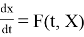
Мы хотим описать эволюцию системы на промежутке времени от
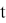
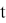
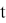
Невозможно знать состояние системы в каждый момент времени, потому что их бесконечно много, а мы будем иметь дело только с конечными числами. Поэтому разделим выделенный интервал времени (
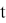
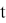
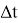
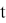
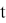
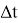
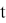
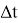
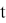
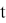
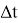
Вычислим значения функций F(
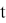
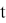
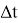
X(
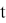
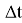
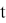
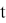
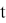
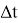
Метод Эйлера несимметричен, поэтому при продвижении на промежутке (t,
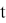
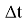
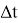
В нашей задаче рассматривается гравитационное взаимодействие космических тел (звезд, центра галактики) и звездолета [1]. В основе расчетов лежит метод Эйлера, где в качестве F(
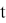
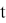

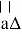
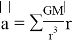
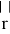
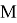
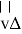

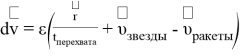
где

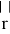
Сфера Хилла — сфера, в которой спутник массивного объекта может удерживать свой спутник [4]. В нашем случае сфера Хилла описывает сферу гравитационного влияния звезды на ракету с учетом возмущения ее траектории под действием центра галактики.
В нашей модели полет звездолета происходит со скоростью около 300 км/c. Для выхода на круговую орбиту с радиусом R = 10 а.е. вокруг выбранной звезды скорость космического аппарата не должна превышать значения равного
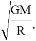
Если силы гравитации звезды не хватит, чтобы погасить набранную ракетой скорость до скорости, позволяющей выйти космическому аппарату на орбиту вокруг звезды, необходимы будут действия для дополнительного торможения ракеты.
Наиболее простым способом осуществления дополнительного торможения ракеты является использование свойства реактивного движения — выброс отработанного топлива в направлении движения космического аппарата. С каждым выбросом топлива изменение скорости ракеты будет происходить на определенный процент от ее начального значения
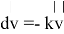
При моделировании траектории движения ракеты в гравитационном поле звезды необходимо учитывать изменение массы космического аппарата в процессе корректировки скорости. Причиной изменения скорости ракеты может быть только сила, действующая на нее со стороны отработанного топлива — реактивная сила, вычисляемая по формуле [2]
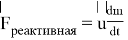
где dm — изменение массы,
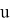
Применим уравнение Мещерского [7], из которого получим
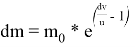
где
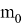
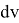
Рассчитаем энергетический выход ядерной реакции гелия-3 — стабильного изотопа гелия, и дейтерия — стабильного изотопа водорода, при использовании их как ракетного топлива.
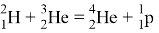
Энергетический выход:
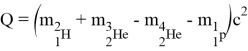
Получим Q =18.8 МэВ. В идеальном случае, вся эта энергия перейдет в кинетическую энергию движения частиц. Тогда оценим, максимально возможную достижимую скорость, в приближении, что энергия между всеми частицами распределилась равномерно:
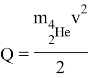
Получим, что скорость выброса достигает 10 % от скорости света. К сожалению, подобную скорость мы не можем получить в реальных условиях, в силу слишком высокой температуры в камере сгорания. Тогда, оценим скорость при температуре
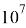
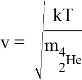
Получим приблизительно 0.001 с , именно это значение скорости истечения мы и будет использовать в нашей программе.
Для визуализации расчетов межзвездных полетов был выбран язык программирования PascalABC.NET, позволяющий постепенно переходить от простейших программ к модульному, объектно-ориентированному, событийному и компонентному программированию.
Наша модель позволяет выбирать характеристики космических объектов (масса, радиус) и параметры орбит космических тел (эксцентриситет, большая полуось, скорость в апоцентре). В качестве цели выбрана звезда с расстоянием в апоцентре 20 тысяч световых лет относительно центра галактики. У Солнца это расстояние 27.7 световых лет. Поэтому примерный путь до звезды составит 7.7 световых лет, что, учитывая разгон и торможение, займет приблизительно 8 млн. лет.
В таблице 1 приведен анализ полученных расчетов к моменту выхода космического корабля на эллиптическую орбиту вокруг звезды (8,25 млн. лет от начала полета).
Таблица 1
Анализ влияния изменения скорости выброса топлива на отношения конечной массы ракеты к начальной
|
Отношение скорости выброса газа к скорости света |
Отношение массы в начале торможения к начальной массе |
Отношение конечной массы к начальной массе |
|
0,0005 |
0,12 |
0,01 |
|
0,0007 |
0,21 |
0,05 |
|
0,0009 |
0,30 |
0,09 |
|
0,001 |
0,33 |
0,12 |
|
0,003 |
0,69 |
0,49 |
|
0,005 |
0,80 |
0,65 |
Данные, полученные с помощью нашей программы, демонстрируют, что увеличение скорости реактивной струи при прочих равных условиях позволяет нам увеличивать оставшуюся в конце полета массу, но никак не влияет на время полёта. Это объясняется тем, что максимальная скорость полёта остаётся постоянной, а именно она отвечает за продолжительность полета.
При уменьшении скорости реактивной струи мы тратим больше времени и топлива на разгон космического аппарата до его крейсерской скорости (таблица 2). Аналогично и с торможением, т. к. чем меньше скорость выброса газа, тем меньше импульс, сообщаемый ракете.
Таблица 2
Анализ влияния крейсерской скорости ракеты на время полета и отношения массы ракеты в начале полета и в конце
|
Отношение максимальной крейсерской скорости к скорости света |
Отношение скорости выброса газа к скорости света |
Отношение массы в начале торможения к начальной массе |
Время полёта, млн. лет |
|
0,0005 |
0,49 |
0,30 |
16,07 |
|
0,0006 |
0,47 |
0,25 |
13,45 |
|
0,0007 |
0,43 |
0,21 |
11,59 |
|
0,0008 |
0,40 |
0,17 |
10,19 |
|
0,0009 |
0,36 |
0,15 |
9,11 |
|
0,001 |
0,33 |
0,12 |
8,25 |
|
0,002 |
0,13 |
0,02 |
4,36 |
|
0,003 |
0,05 |
0,004 |
3,07 |
Из таблицы 2 видно, что оставшаяся масса топлива обратно пропорционально зависит от максимальной скорости ракеты. Продолжительность полёта зависит экспоненциально от максимальной скорости ракеты.
Расчет показывает, что траектория звездолета относительно ядра галактики (рис. 1) не является эллиптической, поскольку она постоянно корректируется с помощью реактивной тяги для скорейшего достижения цели. На рис. 1 также представлена траектория движения ракеты в сфере Хилла звезды. Нам удалось выйти на вытянутую эллиптическую орбиту вокруг звезды. Такая орбита позволит не только исследовать территорию около звезды и осуществить подлёт непосредственно к ней, но и изучить её планетную систему.
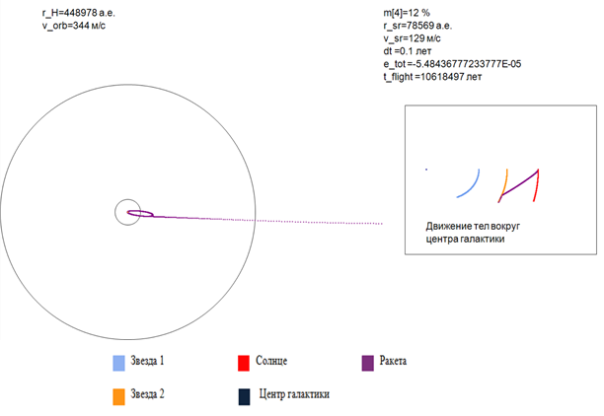
Рис. 1. Пример траекторий тел относительно ядра галактики (в прямоугольнике справа) и траектории звездолёта относительно цели при пересечении сферы Хилла и сферы исследования (слева)
При расчете траектории корабля, мы брали во внимание, то, что корабль будет непилотируемым, так, в нашей модели рассмотрен полет в один конец, осуществляемый в 3 этапа — разгон, движение в крейсерском режиме и торможение. Начало полета осуществляется с околоземной орбиты, далее движение с постоянной реактивной тягой, но переменной длительностью ее включения, для достижения максимальной скорости аппарата. Направление скорости корректируется так, чтобы достичь границы сферы Хилла звезды. На третьем этапе мы производим торможение до достижения ракетой орбитальной скорости в выбранной области.
Для расчета приращения скорости и радиус-векторов объектов, входящих в систему (Солнце, центр галактики, звезды, космический аппарат) мы использовали метод Эйлера. Его погрешность пропорциональна шагу по времени.
Осуществление межзвездного полета — это многоэтапная деятельность по достижению цели. Одним из этапов является разработка компьютерной модели. В нашей работе мы создали упрощенный алгоритм, позволяющий выполнять расчет траектории космического аппарата при движении от одной звезды к другой при быстрой настройке модели на новый объект изучаемого класса, с дальнейшей возможностью оптимизации параметров межзвездного полета, позволяющей выявить оптимальные технические характеристики космического аппарата.
Литература:
- Горина А. Ученые рассказали о перспективах межзвездных перелетов. — Текст: электронный // Сетевое издание «Смотрим»: [сайт]. — URL: https://smotrim.ru/article/1385069 (дата обращения: 23.05.2021).
- Реактивное движение — Текст: электронный // Реальная физика. Реактивное движение [сайт]. — URL: http://bourabai.ru/physics/jet.html#:~:text=Величина %20называется %20реактивной %20силой %20тяги,в %20сторону %2C %20противоположную %20относительной %20скорости (дата обращения: 23.05.2021).
- Термоядерные реакции — Текст: электронный // Большая советская энциклопедия: [сайт]. — URL: https://www.booksite.ru/fulltext/1/001/008/110/168.htm (дата обращения: 23.05.2021).
- Точки Лагранжа и сферы Хилла, как свидетельства взаимо-центризма — Текст: электронный // Новости про космос и НЛО — kosmos-x.net.ru: [сайт]. — URL: http://kosmos-x.net.ru/publ/kosmos/tochki_lagranzha_i_sfery_khilla_kak_svidetelstva_vzaimo_centrizma/12–1–0–247 (дата обращения: 23.05.2021).
- Ученые поделились перспективами межзвездных перелетов — Текст: электронный // ОКО ПЛАНЕТЫ: [сайт]. — URL: https://oko-planet.su/science/scienceday/197985-uchenye-podelilis-perspektivami-mezhzvezdnyh-pereletov.html (дата обращения: 04.04.2021).
- Эйлер Л. Интегральное исчисление: В 3-х томах. Том 1. Москва: ГИТТЛ. 1956. — Текст: электронный // BookReader — Самая большая электронная читалка рунета: [сайт]. — URL: http://bookre.org/reader?file=327692&pg=3 (дата обращения: 23.05.2021).
- Яковенко В. Я. Лекция № 8 Движение тела переменной массы. Уравнения Мещерского и Циолковского. Работа силы, мощность, энергия. Консервативные и неконсервативные силы и системы. Кинетическая и потенциальная энергия — Текст: электронный // Кафедра общей и теоретической физики физико-математического факультета. Белорусский государственный педагогический университет имени Максима Танка [сайт]. — URL: https://phys.bspu.by/static/um/phys/meh/lekcii/lekmexpdf/lekmex_8.pdf (дата обращения: 23.05.2021).

