Ключевые слова: физика, математика, модель, вселенная, граф, подход, адаптация.
Недавно я прочитал статью Стивена Вольфрама «Кажется, мы близки к пониманию фундаментальной теории физики, и она прекрасна» [1, 2].
Стивен Вольфрам — британский физик, математик, программист и писатель, разработавший немалоизвестный язык Wolfram Language и базу знаний Wolfram Alpha, помогающую многим из нас в решении некоторых математических проблем, но новый его проект не сравнится ни с чем разработанным им до этого. Стивен Вольфрам заявил, что он собирается разработать единую модель вселенной. Величайшие умы 20–21 веков бились и бьются над единой теорией физики — «Теорией всего» которая объединила бы Эйнштейновскую Общую и Специальную теории относительности с квантовой механикой, но никому пока это не удалось. Вольфрам решил подойти к этой неразрешимой пока проблеме не со стороны физики и математики, а со стороны информатики и программирования. Эта статья как никогда актуальна, в ней сочетается все, что сейчас так интересует всех: громкое название «Теория Всего» и программирование, которое переживает пик своей популярности.
Цель моей работы заключается в том, чтобы объяснить данную статью более широкой аудитории, чтобы она была доступна людям, которые не имеют специального образования в информатике, физике и математике. Статья содержит не просто новую физическую теорию, а новый подход в науке: построенная научная модель, по мнению Стивена Вольфрама, объясняет простыми законами сложные эффекты, позволяя получать из простых формул объяснение для целых разделов физики.
Но несмотря на такую, казалось бы, доступность, затронув что-то настолько фундаментальное и сложное, невозможно обойтись простыми терминами и понятиями. В своей работе я объясняю основу теории всего, поясняя понятия и термины так, чтобы текст был доступен ученику 10 класса [3].
Для более удобного понимания статьи я объясню несколько терминов заранее.
Граф — это набор вершин, некоторые пары которых соединены рёбрами. В рассматриваемой в работе теме встречаются только ориентированные графы: это графы, рёбра которых имеют имеют направление.
Гиперграф — это более общий вид графа: в нём каждым ребром могут соединяться не только две вершины, но и любые подмножества множества вершин. Другими словами и очень грубо говоря, гиперграф может соединять не только две вершины (как обычный граф), а более двух. Рассмотрим пример гиперграфа на рис. 1. Он содержит 6 вершин (A, B, C, D, E, F) и 4 гиперребра: одно из них соединяет вершины A, B и C, другое — A, F, E, третье — E, D, C, а четвёртое — E, C, A.
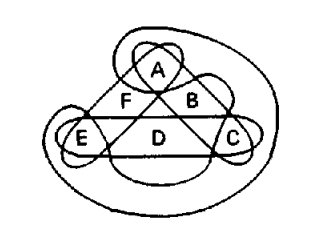
Рис. 1. Пример гиперграфа
Остальные сложные моменты я буду комментировать далее по ходу объяснения основ.
Общие принципы:
Объяснение работы модели начинается с простого множества абстрактных отношений между абстрактными элементами. Что же такое отношение? В школьной программе мы чаще всего рассматриваем частный вид отношения — функцию. У функции есть условие: одному иксу соответствует только один игрек. В данном случае у отношения нет такого условия. Представим это множество абстрактных отношений в виде графа. Допустим, у нас есть множество отношений:
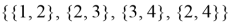
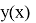
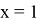
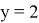
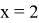
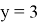
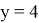
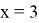
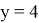
Описанное выше множество будет выглядеть на графе таким образом (рис. 2).
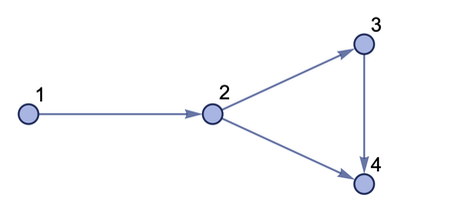
Рис. 2. Множество, изображенное на графе
Все, что здесь определяется графом и множеством отношений — это отношения между элементами и порядок элементов внутри каждого отношения (например,
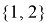
Далее применим к этим графам много раз простое правило. Для примера возьмём такое:
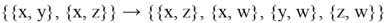
Это правило гласит, что мы должны взять два отношения из множества и проверить их на соответствие образцу
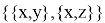
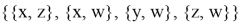
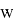
Представим эту трансформацию как операцию над графами (да, это правило, по сути, является такой же операцией, как и привычные нам арифметические операции сложения, умножения и др. над числами, только данная операция определена для графов и совершается над графами) (рис 3).
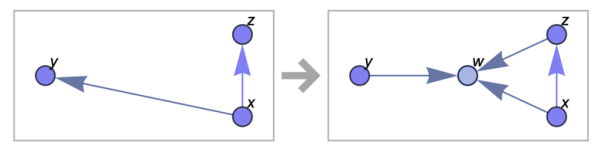
Рис. 3. Операция над графами
Теперь рассмотрим, как изменится множество, которое мы рассматривали, после данной операции:
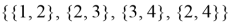
Отношения
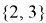
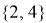
{{1, 2}, {3, 4}, {2, 4}, {2, 5}, {3, 5}, {4, 5}}
Мы можем представить результат в виде графа (он нарисован его перевернутым по отношению к изначальному) (рис 4).
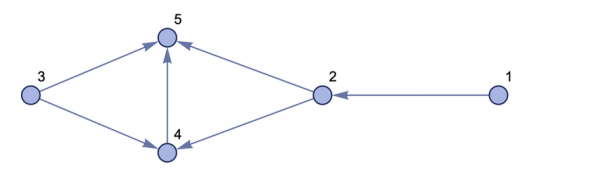
Рис. 4. Перевернутый граф
Далее, мы применяем это правило к нашему множеству рекурсивно — простыми словами каждый раз, получая новое множество, применяем к нему это правило еще раз. В результате получим графы такого вида (рис 5).
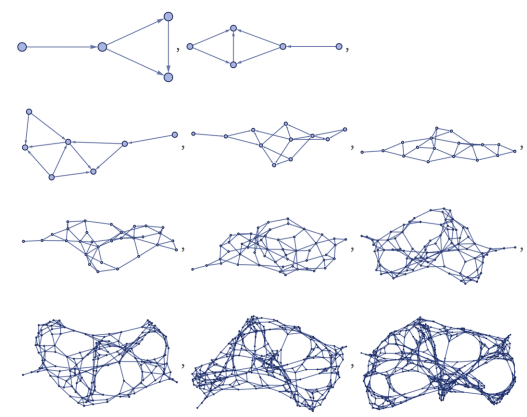
Рис. 5. Графы, иллюстрирующие рекурсивное применение правила на абстрактном множестве
Проделав эту же операцию еще пару раз, получим следующую картину (рис 6):

Рис. 6. Граф, иллюстрирующий множество, к которому много раз было применено одно и то же правило
Мы можем наблюдать, как рекурсивное применение очень простого правила порождает структуру, которая выглядит очень сложно. Такое контринтуитивное, спонтанное зарождение сложности встречается часто при применении очень простых правил к очень простым структурам. Подробнее почитать об этом феномене можно в книге «A New Kind of Science» Стивена Вольфрама.
Далее именно из таких простых структур будут выводится принципы работы нашей Вселенной. Повторим вкратце то, что мы сделали. Мы взяли простое множество абстрактных отношений и стали рекурсивно применять к нему простое правило преобразования. Однако результат преобразования нельзя назвать простым, а самое главное — мы можем заметить у него некоторую форму.
Правило, которое в точности отражает нашу вселенную нам еще не известно, но это точно не то правило, которое мы только что рассматривали. Поэтому дальше мы посмотрим на то, какие возможные правила существуют, и что из них получается.
Для правила, которое мы рассматривали, было характерно то, что оно работает с множествами бинарных отношений, то есть привычных нам по урокам алгебры отношений, которые отражают зависимость только двух параметров —
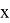
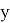
Для иллюстрации будем использовать гиперграф (рис 7).
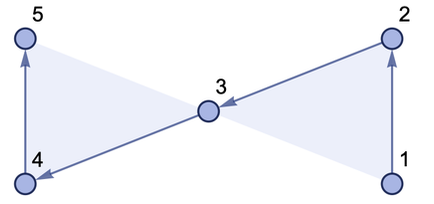
Рис. 7. Гиперграф
Закрашенные области означают, какие точки объединены гиперребром.
Так же, как в предыдущем случае задаем правило, только теперь — для гиперграфа:
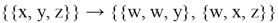
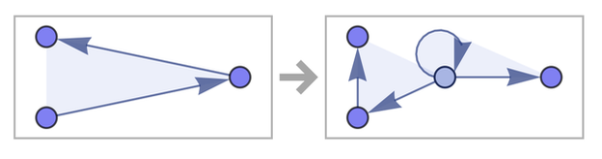
Рис. 8. Иллюстрация с помощью гиперграфа работы правила на троичном отношении
Применим это правило к простейшему возможному троичному множеству {{0,0,0}}. (Здесь на всякий случай поясню, почему слева и справа двойные фигурные скобки. Дело в том, что {0, 0, 0} — это отношение, но мы рассматриваем не отдельно отношение, а множество, в котором оно содержится, но так как оно не содержит ничего, кроме данного отношения, получаем {{0, 0, 0}}). Вот так это будет выглядеть (рис 9):
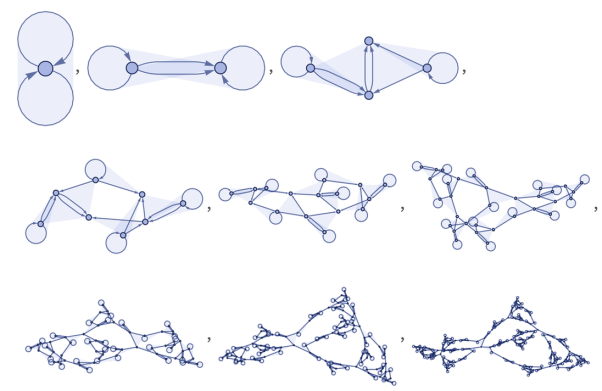
Рис. 9. Применение исходного правила к простейшему троичному множеству {{0,0,0}}
Но простых правил существует очень много. Что же будет, если мы начнем применять различные случайные простые правила? Вот некоторые результаты таких применений (рис 11.):

Рис. 10. Результат применения случайных простых правил на множестве, изображенный с помощью гиперграфа
В результате получаются структуры, которые удивительно напоминают формы простейших организмов и клеточных органелл. На самом деле мы можем увидеть здесь несколько общих форм поведения, различных по сложности.
Главный вопрос состоит в следующем: если мы будем применять рекурсивно эти правила достаточно долго, выдадут ли они нам результат, воспроизводящий нашу физическую вселенную? Если же эти математические структуры, вычисляемые по простым правилам, соответствуют нашей вселенной — как мы в этом удостоверимся? Ведь структуры, которые видны на картинках выше — это результат нескольких тысяч итераций, то есть повторений одного и того же действия. В нашей Вселенной их было произведено около
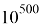
Также здесь есть следующая проблема: феномен вычислительной несократимости. Вкратце он звучит так — даже зная точное правило, по которому работает система, невозможно понять, как она работает, не выполняя каждый шаг вычисления. Иными словами, мы не всегда можем предсказать состояние системы на несколько шагов вперед, не проделывая последовательно каждый шаг. В связи с этим существует эмпирический закон, который заключается в том, что почти во всех случаях, где поведение системы не очевидно простое, алгоритмы, используемые для расчета системы после определенного количества итераций, требуют большей вычислительной мощности, чем та, которая требуется для осуществления всех этих итераций.
Почему же это является проблемой в нашем случае? Опять же, из-за огромного количества итераций, которое прошла вселенная с начала своего существования. Однако, по словам Стивена Вольфрама, мы знаем, что несмотря на наличие областей вычислительной несократимости, областей вычислительной сократимости содержится бесконечное количество.
Подводя итоги своей недавней статьи о теории всего, Вольфрам говорит о том, что несмотря на все технические сложности поиска фундаментальной теории физики, которые связаны с вычислительной несократимостью и другими проблемами, в результате им был найден правильный путь для осуществления цели. Для интересующихся проектом, помимо принципиально нового подхода к науке, возможно, будет интересно то, что работа над поиском фундаментальной теории ведется в открытую. Все, что делает его команда, транслируется или записывается и идет в открытый доступ, так что заинтересованные люди могут наблюдать за проектом, или непосредственно в нем участвовать.
Заключение
В данной работе я объяснил основы теории всего, описанные Стивеном Вольфрамом в рамках его проекта «The Wolfram Physics Project», разъясняя моменты, которые могут быть непонятны учащимся школ и людям, не имеющим специального образования в области физики, математики и информатики. Все интересующиеся могут продолжить ознакомление с теорией всего по статьям Стивена Вольфрама и его коллег в рамках проекта.
Литература:
- Stephen Wolftam: сайт. — URL: https://writings.stephenwolfram.com/2020/04/finally-we-may-have-a-path-to-the-fundamental-theory-of-physics-and-its-beautiful/ (дата обращения: 09.12.2020)
- Хабр: сайт. — URL: https://habr.com/ru/post/518206/ (дата обращения: 09.12.2020)
- Корпорация Российский учебник: сайт. — URL: https://rosuchebnik.ru/metodicheskaja-pomosch/materialy/klass-10_type-rabochaya-programma/ (дата обращения: 09.12.2020)










