В статье рассматриваются математические модели распространения веществ, возникших в области в результате биологических, химических и ядерных атак.
Ключевые слова: РХБЗ, задачи массопереноса, математическая модель распространение веществ в результате взрыва.
Радиационная химическая и биологическая защита (РХБЗ) — является составной частью боевого обеспечения боевых действий войск и представляет собой комплекс мероприятий, организуемых и осуществляемых с целями максимального снижения потерь войск и обеспечения выполнения поставленных задач при действии в условиях РХБ заражения, а также для повышения их защиты от высокоточного и других видов оружия.
РХБЗ среди прочих включает в себя следующие мероприятия: засечку ядерных взрывов, радиационную, химическую, биологическую разведку (РХБР), сбор, обработку данных и информацию о РХБ обстановке.
Говоря об актуальности и новизне данной научно-исследовательской работы, можно отметить, что в ней рассматриваются математические модели распространения веществ, возникших в области в результате биологических, химических и ядерных атак.
Перейдем к математической постановке задачи с мгновенным источником.
В прямоугольной области
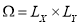
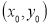
Рис. 1. Направление ветра
Рассматривается уравнение «конвекции-диффузии-реакции», представляющее перенос примеси в заданном потоке вида:
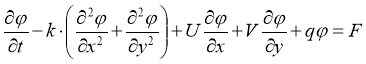
где — концентрация примеси,
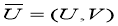
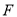
параметр
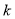
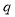
В рассматриваемых нами экспериментах мы выбирали модельные области такого размера, что вещество на момент проведения эксперимента до границ области не долетает, а находится в какой-то внутренней подобласти. Кроме того, в начальный момент времени концентрация вещества в области равна нулю.
Таким образом, начальные и граничные условия имеют:
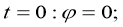
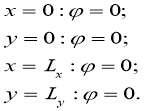
Задача вида (1) — (2) называется прямой задачей для уравнения конвекции-диффузии-реакции. Она связана с необходимостью найти решение внутри заданной области, удовлетворяющее заданному уравнению и заданным начальным и граничным условиям.
Перейдем к рассмотрению численного алгоритма решения рассматриваемой задачи. Для решения задачи (1)-(2) будем использовать метод конечных разностей.
В рассматриваемой в области введем равномерную сетку с шагом
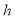
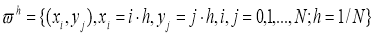
Введем так же сетку по времени:
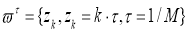
Затем заменим функции непрерывного аргумента на сеточные функции, аппроксимируя производные
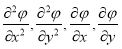
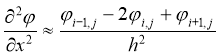
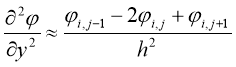
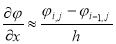
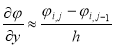
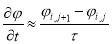
функцию
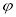
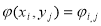
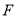
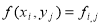
Тогда уравнение (1) принимает вид:
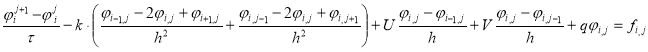
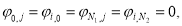
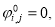
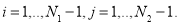
В итоге, наша задача свелась к системе линейных алгебраических уравнений с разреженной, несимметричной, формально пятидиагональной матрицей, для решения которой мы использовали метод пятидиагональной прогонки.
В специализированной среде программирования и на языке MatLab R2014b нами был разработан программный комплекс «Решение задач конвекции-диффузии-реакции». Для этого проекта были созданы несколько подпрограмм, каждая из которых может работать независимо и решать задачи с разными входными данными, так и в общем комплексе, считая конкетную задачу с одним набором данных.
Для тестирования численных схем, рассмотренных в работе, была выбрана задача с известным аналитическим решением.
Были рассмотрены случаи, когда в области находится постоянно действующий источник заражения (стационарная задача) и случаи, когда в области действует мгновенный источник, попавший в область из вне (нестационарная задача).
В первом случае более простом случае для моделирования случае мы исследовали поведение вещества в зависимости от термогидродинамических параметров уравнения и функций, описывающих плотности источников.
Во втором — поведение вещества с течением времени при различных скоростях ветра.
Рассмотрим тесты 1 группы. Задача численно решалась в единичном квадрате. Использовались разные равномерные сетки: крупные, ключающие в себя 10х10 и 20х20 узлов, а также мелкие сетки, состоящие из 50х50 и большего числа узлов.
В качестве теста для задач 1 группы выбиралось точное решение
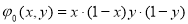
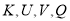
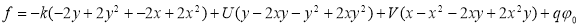
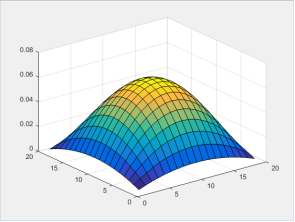

На рисунках 3–5 представлено численное решение стационарной задачи при различных наборах коэффициентов уравнения на сетке 20x20x20 узлов.
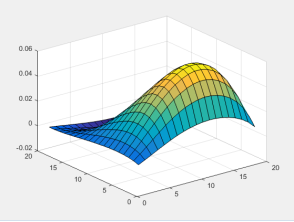
Рис. 3. Поверхность вычисленного решения при K=1, U=10, V=0, Q=1
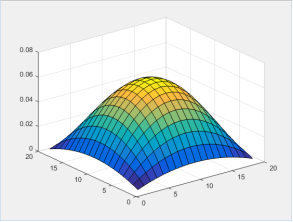
Рис. 4. Поверхность вычисленного решения при K=1, U=0, V=0, Q=1
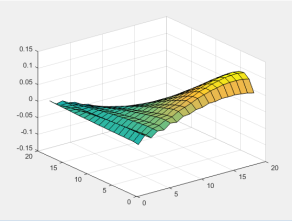
Рис. 5. Поверхность вычисленного решения при K=0,01, U=10, V=1, Q=1
В ходе проведенных экспериментов для тестов 1 группы было выявлено:
- При отсутствии ветра задача решается абсолютно точно, даже при малом коэффициенте диффузии;
- При появлении хотя бы одного из компонент ветра скорости задача решается немного хуже, т. к. происходит «снос» вещества под действием ветра;
- При присутствии обоих компонент скорости, особенно когда они достаточно большие, а также при достаточно малом коэффициенте диффузии, задача решается с большими погрешностями.
Перейдем к рассмотрению задач группы 2.Вкачестве тестов для задач этой группы выбиралось точное решение:
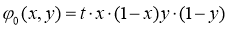
Задавались параметры уравнения, правая часть определялась формулой:
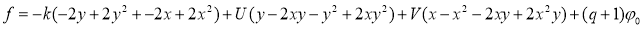
Задача решалась на сетке 40x40x40 узлов.
На рисунках 6 и 7 представлены поверхности, описывающие распределение вещества в области с течением времени при разных значениях коэффициентов. Слева — точное решение задачи, справа — вычисленного при расчетах решения. Данные выводятся на последнем временном отрезке.
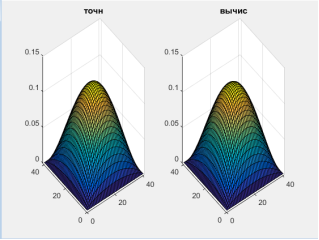
Рис. 6. Поверхность точного и вычисленного решения при K=0.5, U=0, V=0, Q=1
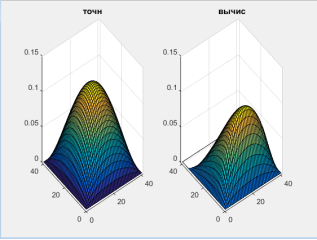
Рис. 7. Поверхность точного и вычисленного решения при K=0.5, U=5, V=0, Q=1
В результате проведенных экспериментов для тестов 2 группы получили:
- Если день безветренный день, то концентрация вещества в области растет, т. к. диффузия маленькая, а потока нет. Т. е. происходит накопление веществ в определённом районе. Для ликвидации последствий это «облако» можно каким-то образом «зацепить» и обезвредить.
- Если день ветренный, то необходимо делать анализ, через какое время вещество достигнет того или иного района и соответственно определяют район эвакуации и готовятся к ликвидации последствий.
В данной научно-исследовательской работе был представлен численный метод решения прямых модельных задач распространения веществ, возникающих в области в результате биологических, химических и ядерных атак, в которых требовалось найти решение внутри заданной области, удовлетворяющее данному уравнению и заданным начальным и граничным условиям. Проведенные вычислительные эксперименты показали близость численного решения к аналитическому, что говорит о корректности представленного метода.
Литература:
1. Алексеев Г. В., Терешко Д. А. Двухпараметрические экстремальные задачи граничного управления для стационарных уравнений тепловой конвекции // Ж. вычисл. матем. и матем. физ. 2011. Т. 51. N 9. С. 1645–1664
2. Калинина Е. А. Численное исследование обратной экстремальной задачи идентификации параметра примеси для модели распространения загрязнений // Фундаментальные науки и образование. Бийск. 2006. С. 95–101
3. Калинина Е. А. Использование схем повышенной точности для численного исследования обратных задач идентификации плотности источника одномерного нестационарного уравнения конвекции-диффузии // Выч. техн. 2004. Т.9. Часть 2. С.287–296

