В 2015 г. народ России праздновал 70 лет со Дня Победы над фашистской Германией, и 97 лет со дня окончания Первой мировой войны. Множество героических подвигов, сражений вспоминаем мы в преддверие этих дат, но ни одна битва не проходила без артиллерийского орудия.
В военных действиях применялись артиллерийские системы призваны выполнить самые разнообразные задачи: уничтожение живой силы и огневых средств противника в наступлении и обороне, подготовка наступления и сопровождение наступающих подразделений, разрушение прочных оборонительных сооружений, уничтожение танков и иных бронированных подвижных целей на поле боя, борьба с артиллерией и авиацией противника и другие.
Многое зависело от типа артиллерийского орудия, его дислокации и расположения целей поражения или объектов противника, наводка орудий проводилась путем изменения положения дула относительно горизонта. Возникает вопрос: «Как влияет угол запуска на дальность полета снарядов артиллерийских орудий?»
Объект — движение тела, брошенного под углом к горизонту.
Предмет — дальности полета, угол запуска снаряда.
Гипотеза: между углом запуска снаряда и дальностью полета существует обратная зависимость (чем больше угол запуска, тем меньше дальность полета).
Цель: установить зависимость дальности полета снаряда от угла запуска.
Исходя из поставленной цели, были определены следующие задачи:
изучить теоретические вопросы движения тела, брошенного под углом к горизонту;
рассмотреть классификацию типов артиллерийских орудий;
экспериментально исследовать зависимость дальности полета «снаряда» (тела) от угла бросания;
В процессе исследования были использованы следующие методы:
теоретические (обзор литературы по указанной теме, анализ полученной информации);
практические;
экспериментальные.
Экспериментальное исследование зависимости дальности полета тела от угла бросания предполагало установление зависимости дальности полета «снаряда» от угла бросания относительно горизонта.
Эксперимент состоял из трех этапов: организационный, экспериментальный, аналитический.
а) Организационный этап
На данном этапе подготавливаем оборудование (штатив, баллистический пистолет, «снаряд» — металлический шарик, копировальная бумага, лист бумаги, сантиметровая лента), определяем формулу.
б) Экспериментальный этап
Для проведения данного этапа устанавливаем штатив (на полу около стола), на штативе закрепляем баллистический пистолет, на стол кладем лист бумаги, сверху — копировальную бумагу. Результаты представлены в Таблице 1.
Таблица 1
Спецификация измерительных приборов
|
Наименование прибора |
Предел измерения |
Цена деления |
Приборная погрешность |
|
Сантиметровая лента |
1,5 |
0,001 |
0,0005 |
Устанавливаем баллистический пистолет под выбранным углом к горизонту (рис. 1), заряжаем пистолет и производим выстрел, после чего измеряем расстояние от пистолета до места падения «снаряда» и заносим значение прямого измерения в таблицу. Результаты представлены в Таблице 2.


Рис. 1. Экспериментальная установка
Изменяя угол наклона баллистического пистолета, проводим выстрелы и измерения дальности полета «снаряда» (для каждого значения угла проводим пять выстрелов и соответственно пять измерений дальности полета). При выполнении эксперимента необходимо выполнять правила безопасности — не стоять на линии полета «снаряда».
Таблица 2
Результаты измерения дальности полета «снаряда» сантиметровой лентой
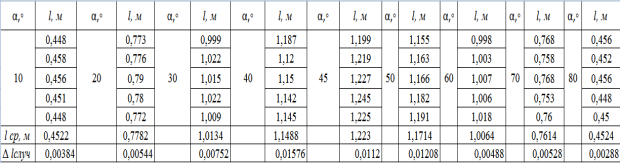
где ![]() — угол запуска «снаряда», l– дальность полета «снаряда», lср — среднее арифметическое значение дальности полета «снаряда»
— угол запуска «снаряда», l– дальность полета «снаряда», lср — среднее арифметическое значение дальности полета «снаряда»
Для вычисления среднего значения дальности полета при указанном значении угла запуска «снаряда» используем формулу (1), полученные косвенные измерения записываем в соответствующие стоки таблиц (2,3).
![]() , (1)
, (1)
Проведем вычисления полной погрешности прямых измерений для каждого значения дальности при конкретном угле по формуле (2):
![]() пр+
пр+ ![]() сл, (2)
сл, (2)
где ![]() пр — приборная (инструментальная) погрешность (из табл.1)
пр — приборная (инструментальная) погрешность (из табл.1)
![]() сл- случайная погрешность, рассчитывается по формуле (3).
сл- случайная погрешность, рассчитывается по формуле (3).
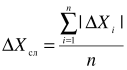 (3)
(3)
Значение результата прямых измерений запишем в соответствие с формулой (4):
х = хср![]() , (4)
, (4)
где ![]() 10 = 0,0043 м,
10 = 0,0043 м, ![]() 20= 0,0059 м,
20= 0,0059 м, ![]() 30= 0,008 м,
30= 0,008 м, ![]() 40 = 0,0163 м,
40 = 0,0163 м, ![]() 45 = 0,0117 м,
45 = 0,0117 м, ![]() 50= 0,0126 м,
50= 0,0126 м, ![]() 60 = 0,0054 м,
60 = 0,0054 м, ![]() 70 = 0,0056 м,
70 = 0,0056 м, ![]() 80 = 0,0034 м.
80 = 0,0034 м.
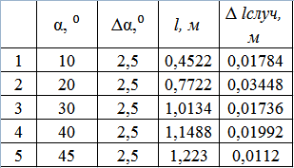
Запишем результаты прямых в Таблицу 3, где выделим столбцы, содержащие приблизительно равные значения дальности полета «снаряда» (для проведения анализа полученных результатов прямых измерений дальности полета «снаряда»).
Таблица 3
Результаты прямых измерений дальности полета «снаряда», брошенного под углом к горизонту
|
α,° |
10 |
20 |
30 |
40 |
45 |
50 |
60 |
70 |
80 |
|
l ср, м |
0,4522 |
0,7782 |
1,0134 |
1,1488 |
1,223 |
1,1714 |
1,0064 |
0,7614 |
0,4524 |
|
|
х = хср |
х = хср |
|
|
10 |
0,4522 |
0,4524 |
80 |
|
20 |
0,778 |
0,7614 |
70 |
|
30 |
1,0134 |
1,0064 |
60 |
|
40 |
1,1488 |
1,1714 |
50 |
|
45 |
1,223 |
|
|
в) Аналитический этап
Анализируя результаты прямых измерений дальности полета «снаряда», брошенного под углом к горизонту формулируем вывод эксперимента.
Между углом запуска «снаряда» и дальностью полета существует зависимость, экспериментально обнаружено:
а) в диапазоне значения углов от 100 до 450 зависимость l(![]() ) прямая — при увеличении значения угла запуска снаряда его дальность полета увеличивается (рис. 2);
) прямая — при увеличении значения угла запуска снаряда его дальность полета увеличивается (рис. 2);
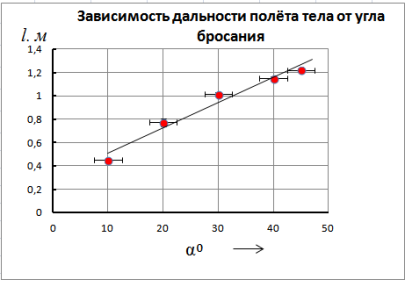
Рис. 2.
б) в диапазоне значения углов от 50 до800зависимость l(![]() ) обратная — при увеличении значения угла запуска снаряда его дальность полета уменьшается (рис. 3).
) обратная — при увеличении значения угла запуска снаряда его дальность полета уменьшается (рис. 3).
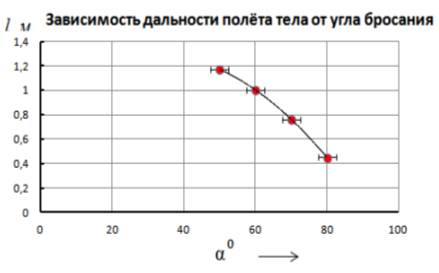
Рис. 3.
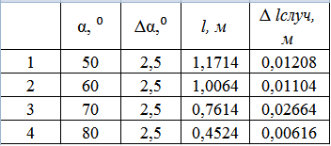
Поясним результаты Таблицы 3: формула (9) отражает зависимость дальности полета от начальной скорости тела и угла запуска, обратим внимание, что в числителе формулы — функция sin2![]() . Используя формулу приведения (5), докажем, что совпадение значения дальности при выделенных углах не случайно (таблица 4).
. Используя формулу приведения (5), докажем, что совпадение значения дальности при выделенных углах не случайно (таблица 4).
![]() (5)
(5)
Таблица 4
Сравнение значений Sin(2![]()
|
|
Sin(2 |
Sin(2 |
|
|
800 |
Sin( |
Sin(2*100) = Sin (200) |
100 |
|
700 |
Sin( |
Sin(2*200) = Sin (400) |
200 |
|
600 |
Sin( |
Sin(2*300) = Sin (600) |
300 |
|
500 |
Sin( |
Sin(2*400) = Sin (400) |
400 |
Значение Sin(2![]() (рис.4)
(рис.4)
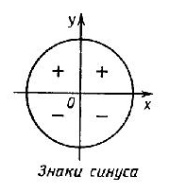
Рис. 4. Знак синуса
Таким образом, на основании полученных результатов можно свидетельствовать, чтогипотеза частично подтверждена, то есть между углом запуска снаряда и дальностью полетаl(![]() ) существует обратная зависимость, но только в диапазоне значений угла от 500 до 800, а в диапазоне значений угла от 100 до 450 обнаружили прямую зависимость l(
) существует обратная зависимость, но только в диапазоне значений угла от 500 до 800, а в диапазоне значений угла от 100 до 450 обнаружили прямую зависимость l(![]() ).
).
Данные зависимости l(![]() ) были использованы на полях сражения при артиллерийских атаках неоднократно с учетом дислокации орудия и расположения цели.
) были использованы на полях сражения при артиллерийских атаках неоднократно с учетом дислокации орудия и расположения цели.
Мы не утверждаем, что артиллеристы знали выражение зависимости l(![]() ) математической формулой, но эти знания приобретались на практике и активно применялись в бою.
) математической формулой, но эти знания приобретались на практике и активно применялись в бою.
Литература:
- «Движение тела, брошенного горизонтально или под углом к горизонту». — Режим доступа: http://www.eduspb.com/node/1669, дата доступа 15.01.2015 г.
- «Изучение движения тела, брошенного под углом к горизонту». — Режим доступа: http://ido.tsu.ru/schools/physmat/data/res/virtlab/text/m2_1.html, дата доступа 15.01.2015 г.
- «Орудие для навесной стрельбы». — Режим доступа: http://universal_ru_en.academic.ru/, дата доступа 24.11.2014 г.
- М. Е. Свирин Классификация артиллерийских систем КА для заинтересованных. — Режим доступа: http://temezhnikov.narod.ru/
- vifrg/20750.htm, дата доступа 24.11.2014 г.

