В школе проходили уроки финансовой грамотности в виде вебинаров. На данных уроках я познакомился с понятием денег, банков, вкладов, кредитов и т. д. Меня заинтересовала одна из тем: «Вклады: как сохранить и приумножить». В ней рассказывалось о банковском вкладе и о том, что деньги, положенные на него, «работают» и сумма вклада увеличивается в соответствии с процентной ставкой. Мне стало интересно как на математическом языке записывается банковский вклад и какие процентные ставки существуют. Изучив литературу и проконсультировавшись с учителем математики по данному вопросу, я пришел к следующему.
Проценты — одно из математических понятий, которое часто встречается в повседневной жизни. Объявления банков, привлекающих деньги населения на различных условиях, об изменении процента банковского кредита… Все это требует умение производить процентные расчеты.
Начисление процента на депозит, процентная ставка или банковский процент — это одно из самых старых и любопытных изобретений человечества. Можно предположить, что начислять процент (процентную ставку) начали еще в далекой древности, одновременно с появлением денег. Хотя известно, что брать взаймы можно не только деньгами. Когда еще господствовал натуральный обмен, и понятия процентной ставки не существовало вовсе, первые кредиты выдавались в виде зерна. Например, один фермер одалживал другому корзину с зерном, а при возврате кредита требовал вернуть корзину зерна, но уже большего объема. Деятельность ростовщиков сделала банковский процент одним из самых важных явлений в современном мире.
Банковский вклад — это денежные средства или ценные бумаги, помещаемые на хранение в банк на определенный срок от имени физического или юридического лица, которому за это начисляется определенный процент. В настоящее время все вклады в банк (депозиты), производимые в целях сохранения и приумножения денег, то есть получения банковских процентов на вложенные средства, можно разделить на две категории:
бессрочные вклады — вклады, которые могут быть востребованы вкладчиком в любой момент;
срочные вклады — денежные вклады, размещаемые в банке на определенный срок, например на 1 год;
По бессрочным вкладам (или вкладам до востребования) банки выплачивают крайне низкие проценты (обычно процентная ставка составляет 0,1 % в год) или не выплачивают их вовсе.
Срочные вклады банки принимают обычно на период от 2, 3, 6 месяцев до 2–3 лет. В этом случае вкладчикам предлагается более высокий банковский процент (процентную ставку), как правило, зависящий от срока вклада и размера вложенных средств. Банки, таким образом, могут распоряжаться этими средствами в течение более длительного времени.
Процентная ставка по вкладу (процент) — это ставка, определяющая вознаграждение, которое получает клиент за размещение своих средств во вклад. Под процентной ставкой обычно подразумевается годовая процентная ставка, а проценты при этом выплачиваются, например, раз в год, квартал или месяц. В этом случае на счет вкладчика будет поступать полная сумма процентов за год либо разделенная на 4 или на 12 в зависимости от периодичности начисления процентов.
Представьте себе, что вы открыли в банке вклад в сумме a руб. под р % годовых на t лет. У вас есть две стратегии поведения: либо в конце каждого года хранения вклада снимать проценты по вкладу, т. е. полученную прибыль в размере
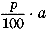
В первом случае при t=1 вы получите
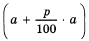
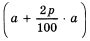
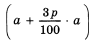
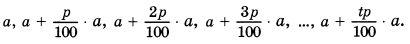
Итак, при первой стратегии поведения за t лет вы получите
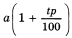
Если вы решили прийти в банк только в конце срока хранения вклада, то при t=1 получаемая сумма составит, как и в первом случае,
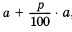
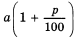
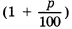
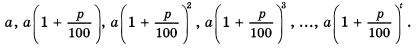
Итак, при второй стратегии поведения за t лет вы получите
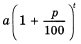
На примере рассмотрим разницу вклада простого процента и сложного процента.
Пусть вклад составляет 100 000 руб. , банк дает 10 % годовых, срок хранения вклада — 5 лет. Если выберем стратегию простых процентов, то к концу срока хранения получим в итоге сумму: 100 000·(1+5·100) = 150 000 руб. Если же выберем стратегию сложных процентов, то к концу срока хранения получим в итоге сумму: 100 000·(1+10/100) 5 = 161 051 руб. Разница: 161 051 руб. — 150 000 руб. = 11 051 руб.
Современная жизнь заставляет быть человека финансово грамотным, он должен разумно распоряжаться денежными средствами, знать принцип работы банковского вклада как инструмента хранения и увеличения денежных средств. Для этого нужно уметь решать экономические задачи на проценты.
Литература:
- https://ru.wikipedia.org/wiki/Банк
- Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов.- 12-е издание., стер.-М.: Мнемозина, 2010–224 с.
- Мир математики: в 40 т. Т. 19: Луис Арталь, Жузеп Салес. Ипотека и уравнения. Математика в экономике. / Пер. с исп. — М.: Де Агостини, 2014. — 160 с.









