Многогранники — удивительные геометрические фигуры, привлекавшие внимание многих выдающихся мыслителей. Теория многогранников является современным разделом математики и тесно связана с топологией. Она имеет большое значение как для теоретических исследований по геометрии, так и для практических приложений в других разделах математики, например, в алгебре и теории чисел, прикладной математике — линейном программировании, теории оптимального управления. Данная работа посвящена изучению полуправильных многогранников, которые широко используются человеком.
Цель работы: с помощью 3D-моделирования с использованием вычислительного эксперимента изучить свойства разных видов полуправильных многогранников.
Задачи работы:
- Изучить виды полуправильных многогранников и их использование в повседневной жизни.
- Разработать алгоритмы моделирования полуправильных многогранников в САПР Компас 3-D.
- По разработанным алгоритмам напечатать 3-D модели полуправильных многогранников и изучить их свойства, применяя вычислительные эксперименты.
Полуправильные многогранники и их виды
Полуправильные многогранники являются естественным расширением пяти видов правильных многогранников (тетраэдра, куба, додекаэдра, октаэдра и икосаэдра). Их изучением начал заниматься Архимед.
Полуправильными многогранниками называются тела, у которых отсутствует только одно из следующих свойств правильных тел:
1) Все грани являются правильными многоугольниками.
2) Все грани равны между собой.
3) Тело относится к одному из трёх существующих типов пространственной симметрии.
Изучены такие виды полуправильных многогранников, как архимедовы тела, каталановы тела и две бесконечные серии — правильные призмы и антипризмы.
- Архимедовы тела — это полуправильные выпуклые многогранники, все многогранные углы которых равны, а грани — правильные многоугольники нескольких типов. Утверждают, что впервые 13 полуправильных выпуклых многогранников перечислил Архимед в не дошедшей до нас работе. Ссылки на эту работу имеются в трудах математика Паппа.
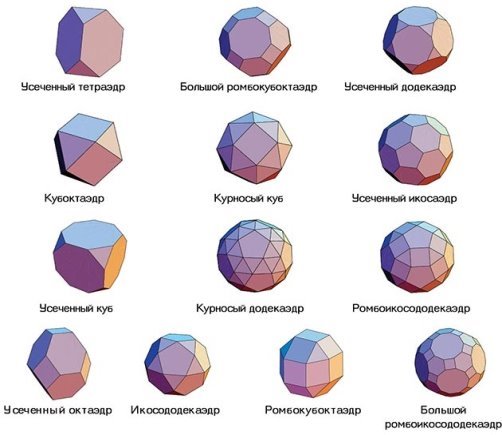
Рис. 1. Архимедовы тела
Множество архимедовых тел можно разбить на пять групп:
1) Пять многогранников, которые получаются из пяти платоновых тел в результате их усечения, т. е. удаления частей многогранника, расположенных около вершины, вместе с самой вершиной. Так получены усеченный тетраэдр, усеченный куб, усеченный октаэдр, усеченный додекаэдр и усеченный икосаэдр.
2) Кубооктаэдр и икосододекаэдр — квазиправильные многогранники. Их гранями являются правильные многоугольники всего двух типов. Каждая грань одного типа окружена гранями другого типа. Для получения кубооктаэдра в кубе проводятся отсекающие плоскости через середины ребер, выходящих из одной вершины. Его гранями являются шесть квадратов, как у куба, и восемь правильных треугольников, как у октаэдра. Аналогично в додекаэдре проводят отсекающие плоскости. Получаем икосододекаэдр. У него двадцать граней — правильные треугольники и двенадцать граней — правильные пятиугольники, то есть все грани икосаэдра и додекаэдра.
3) Четыре тела — ромбокубоктаэдр и ромбоикосододекаэдр, получаемые усечением кубоктаэдра и икосододекаэдра. В эту же группу входят ромбоусеченный кубоктаэдр и ромбоусеченный икосододекаэдр, которые получаются из тех же многогранников при другом варианте усечения.
4) Курносый куб и курносый додекаэдр. Для них характерно повернутое положение граней. Эти многогранники, в отличие от предыдущих, не имеют плоскостей симметрии, но имеют оси симметрии. Так как плоскостей симметрии нет, то зеркальное отражение такого тела не совпадает с исходным телом, и поэтому существуют по две формы каждого из них — «правая» и «левая», отличающиеся так же, как правая и левая руки.
5) Единственный многогранник — псевдоромбокубоктаэдр (многогранник Джонсона), открытого лишь в XX веке. Он может быть получен из ромбокубоктаэдра, если повернуть одну из восьмиугольных чаш на 45°. Иногда тело не причисляют к списку архимедовых тел, т. к. многогранник не обладает глобальной симметрией, переводящей любую вершину в любую другую.
- Каталановы тела
Двойственные архимедовым телам, так называемые каталановы тела, имеют равные грани, равные двугранные углы и правильные многогранные углы. Как и архимедовы тела, каталановы тела насчитывают 13 фигур.
Правильные призмы и антипризмы — это выпуклые однородные многогранники, имеющие гранями несколько различных выпуклых многоугольников. Первым математиком, начавшим изучение призм и антипризм, был Кеплер (1619г). Он заметил, что призмы и антипризмы относятся к архимедовым телам, но их не всегда таковыми считают ввиду исторических соображений симметрии.
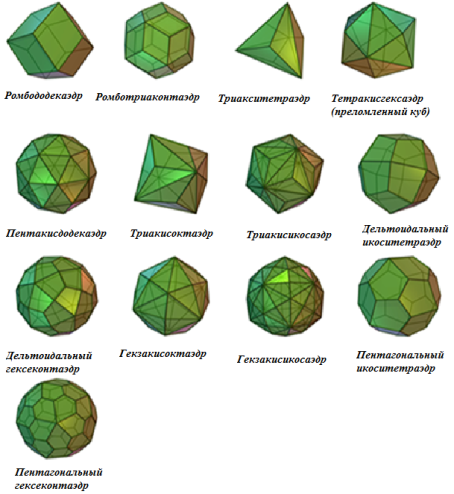
Рис. 2 Каталановы тела
Правильная призма — это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы — равные прямоугольники. Именно правильные призмы образуют одну из двух бесконечных последовательностей полуправильных многогранников, другую последовательность образуют антипризмы — полуправильные многогранники, у которых две параллельные грани (основания) — равные между собой правильные n-угольники, а остальные 2n граней (боковые грани) — правильные треугольники. Антипризма получается, если повернуть одно основание призмы относительно другого и поочередно, зигзагом, соединить вершины. В каждой вершине антипризмы встречаются четыре грани –основание и три боковых треугольника.
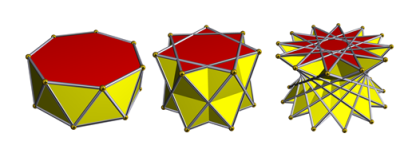
Рис. 3. Антипризмы
Сферы применения полуправильных многогранников
Искусство
Ещё в 15 веке великие художники начали изображать полуправильные многогранники на своих картинах. Например, усечённый икосаэдр можно увидеть в книге Луки Пачоли «О божественной пропорции». Эту книгупроиллюстрировал всеми известный художник и учёный — Леонардо да Винчи. На единственном известном портрете Луки Пачоли, автором которого был Якопо де Барбари, мы видим уже знакомую нам фигуру — ромбокубоктаэдр.
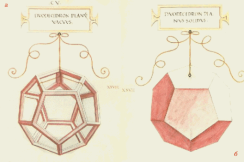

Рис. 4
Архитектура
Использовать многогранники в архитектуре люди стали очень давно, еще до новой эры. И по мере роста строительного мастерства в мире появлялись новые шедевры, основанные на более сложных видах многогранников.
Самым ярким примером использования архимедовых тел является Национальная библиотека Беларуси. Еще в 1989 году был проведен всесоюзный конкурс на лучший проект будущего книгохранилища. Его победители предложили модель «белорусского алмаза», в котором сочетались функциональность и современный дизайн. Идея предполагала возведение оригинального здания в виде ромбокубооктаэдра, расположенного на подставке-подиуме. В основе дизайна музея архитектуры Тойо Ито на острове Омишима (Япония), также лежат геометрические фигуры: октаэдр, тетраэдр и кубооктаэдр.


Рис. 5
Обтекатель антенны наземной станции системы спутниковой связи в Антарктиде выполнен в виде каталанова тела — пентакисдодекаэдра. Пять лет назад ввели в эксплуатацию офисное здание, построенное в форме квадратной антипризмы, на Малоохтинском проспекте в городе Санкт-Петербург. Оно образовало архитектурный ансамбль с расположенным неподалеку бизнес-центром банка «Санкт-Петербург».


Рис. 6
Интерьер
Геометрические элементы были характерным декоративным мотивом в далёкие 60-е годы. Сегодня их используют в основном в интерьерах, оформленных в современном стиле или же в эклектике. Полуправильные многогранники получили свою известность именно в последнее десятилетие, в их форме делают различные светильники, люстры, кашпо.


Рис. 7
Природа
Как уже было сказано ранее, многогранники часто можно встретить в природе. Форму усечённого икосаэдра имеет молекула фуллерена C60, в которой 60 атомов углерода соответствуют 60 вершинам этого многогранника. Горный хрусталь, также имеет форму одного из полуправильных многогранников — правильной призмы.
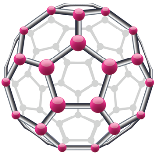

Рис. 8
Другие сферы использования
Некоторые каталановы и архимедовы тела используются в качестве игральных костей в некоторых настольных играх. Классический футбольный мяч имеет форму уже всем известного усечённого икосаэдра (если представить его пятиугольники и шестиугольники, обычно окрашенные соответственно чёрным и белым, плоскими).


Рис. 9
Моделирование полуправильных многогранников в САПР КОМПАС-3D
Пятиугольная антипризма — это третья в бесконечном ряду антипризм, образованных чётным набором треугольных сторон и закрытых с обеих сторон двумя многоугольниками. Она состоит из двух пятиугольников, связанных друг с другом кольцом из 10 треугольников.
Алгоритм 3 D моделирования пятиугольной антипризмы в САПР Компас:
- Построить правильный пятиугольник;
- В параллельной плоскости построить пятиугольник, повернув данный на 180°;
- Последовательно соединить вершины многоугольников.
Процесс создания пятиугольной призмы:
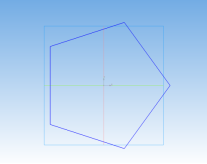
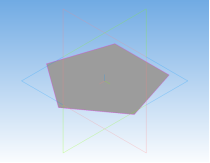
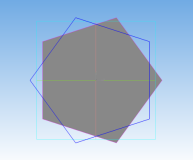
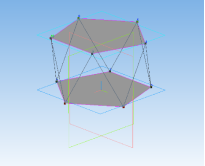
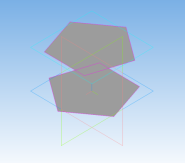

Рис. 10
Вычислительный эксперимент показал, что важным свойством антипризмы является равенство всех треугольников, составляющих боковую поверхность.
Антипризма 15/7
Не имеет определённого названия: обозначение 15/7 означает, что основания антипризмы — пятнадцатиконечные звёзды, а между двумя равными гранями треугольников, из которых она состоит, находится 6 вершин звезды.
Алгоритм 3 D моделирования антипризмы 15/7:
- Построить пятнадцатиконечную звезду;
- В параллельной плоскости построить вторую такую звезду, повернув данную на 180°;
- Последовательно построить равнобедренные треугольники, соединяя вершины звёзд (в верхней звезде провести первое ребро (основание) треугольника так, чтобы оно разделило её на две стороны: в одной — 6 конечностей, во второй — 7; затем со стороны, где оказалось их 6, провести к нижнему основанию ещё два равных ребра). Повторить этот шаг со всеми вершинами оснований антипризмы.
Получение антипризмы 15/7:
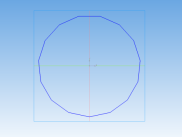
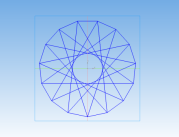
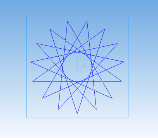
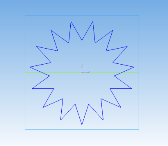

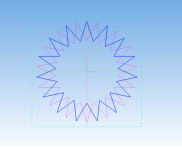
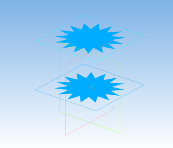
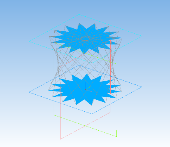

Рис. 11
Вычислительный эксперимент показал, что все плоские сечения, проходящие через три вершины оснований по указанному в алгоритме правилу, являются равными равнобедренными треугольниками.
Ромбоусечённый кубооктаэдр –архимедово тело с 12 квадратными гранями, 8 гранями в виде правильного шестиугольника и 6 гранями в виде правильного восьмиугольника. Двугранный угол между каждым квадратом и основанием (правильным восьмиугольником) равен 135°, между шестиугольником и восьмиугольником — 125°, между квадратом и шестиугольником — 145°.
Процесс создания ромбоусечённого кубооктаэдра:
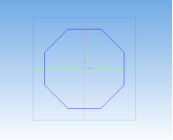
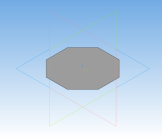
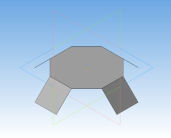
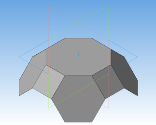
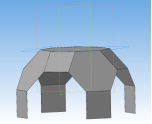
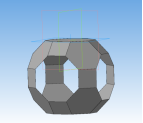
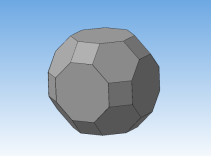
Рис. 12
Величины всех двугранных углов установлены с помощью вычислительных экспериментов.
Гекзакисоктаэдр — каталаново тело, двойственное ромбоусечённому кубооктаэдру. Составлен из 48 одинаковых разносторонних остроугольных треугольников с углами 55,03°, 37,77° и 87,20°. Двугранный угол при каждом ребре равен 155,08°. Алгоритм 3D моделирования гекзакисоктаэдра аналогичен алгоритму моделирования предыдущих фигур.
Создание гекзакисоктаэдра:

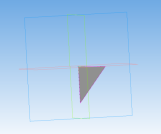
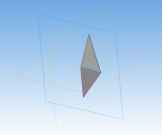
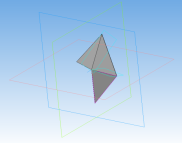
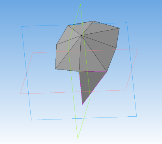
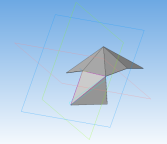
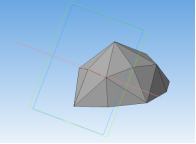

Рис. 13
3D-печать полуправильных многогранников
Модели полуправильных многогранников в ходе дальнейшей исследовательской работы напечатаны на 3-D принтере по разработанным алгоритмам.



Рис. 14. Пятиугольная антипризма



Рис. 15. Четырехугольная антипризма

Рис. 16. Антипризма 15/7

Рис. 17. Гекзакисоктаэдр

Рис. 18. Ромбоусечённый кубооктаэдр
В процессе проведенного учебного исследования получены новые теоретические знания в области информатики и математики, проанализированы свойства различных видов полуправильных многогранников, самостоятельно разработаны алгоритмы создания 3D-моделей этих фигур, улучшены навыки пространственного мышления и рассмотрены методы построения многогранников с помощью САПР Компас 3-D.
Изучение таких фигур, как полуправильные многогранники, действительно способно развивать пространственное мышление. Этот навык помогает не только математикам и физикам решать сложные задачи, но и дизайнерам и архитекторам, строителям, художникам, модельерам, всем людям тех профессий, которые имеют непосредственное отношение к пространству и расположению в нем объектов. Например, режиссерам и операторам, проводящим огромную мыслительную работу, «располагая» актеров и объекте на сцене, и многим другим.
Мир полуправильных многогранников велик и разнообразен, каждый их вид и подвид интересен и уникален. Именно поэтому стоить уделять внимание изучению этих фигур.
Литература:
- Баранова И. В. КОМПАС-3D для школьников. Черчение и компьютерная графика. — М.: ДМК Пресс, 2009
- Герасимов А. В. Самоучитель КОМПАС-3D V12. -2011.
- ЗАО Аскон Азбука Компас 3D. Учебное пособие. –АСКОН, КОМПАС, 2014
- Каченовский М. И. Математический практикум по моделированию. -2009.
- https://ru.wikipedia.org/
- http://school-37.ru/
- https://e-koncept.ru/
- https://studopedia.ru/
- https://mnogogranniki.eto-ya.com/
- http://www.wikiwand.com












