В своей повседневной жизни мы часто сталкиваемся с задачами, которые связаны с вычислением периметра, то есть суммы длин сторон различных геометрических фигур. В случае, если геометрическая фигура — многоугольник, нахождение его периметра не составляет особого труда: для этого достаточно с помощью линейки измерить длину каждой из сторон и сложить полученные результаты. Что же делать, если необходимо узнать длину окружности? Ответу на этот вопрос посвящена данная статья.
Окружность является самой распространённой кривой практически во всех областях человеческой деятельности. Форму окружности или круга мы встречаем повсюду: это и колесо машины, и линия горизонта, и диск Луны. Многие вещи, окружающие нас, имеют круглую форму, например: обруч, кольцо, мяч, тарелка.
В свободное время я люблю заниматься моделированием из бумаги, пластилина и, особенно, из деталей конструктора Лего. Иногда, для того чтобы подготовить нужную заготовку для модели, необходимо знать длину сторон фигуры, которую хочешь получить. Никогда эта задача не вызывала у меня затруднений, пока я не столкнулся с определением длины окружности.
В учебнике по геометрии 7 класса рассматривается вопрос определения длины окружности. Существует формула, при помощи которой решается эта задача. Мне стало интересно, а как же раньше, в древности, люди находили длину окружности, можно ли ее найти экспериментальным путем без помощи известной формулы, какая существует связь между размером окружности (диаметром) и длиной окружности, и какое практическое применение может иметь решение этой задачи.
Ещё в давние времена люди сталкивались с практическими задачами, для решения которых необходимо было уметь находить длину окружности. Например, для того чтобы изготовить металлический обод для колеса телеги, определить вместительность сосуда, при строительстве зданий, для изготовления ювелирных изделий, при пошиве одежды.
В источниках [1, 4] сказано, что уже 4 тысячи лет назад люди знали, что длина окружности примерно равна трём его диаметрам. В дальнейшем, более 2 тыс. лет назад, большой вклад в развитие геометрии, в том числе в изучение геометрических фигур — окружности и круга — внесли древнегреческий математик Евклид, а позже — Архимед.
Целью исследования является изучение различных способов нахождения длины окружности и получение взаимосвязи между диаметром окружности и её длиной.
Гипотеза исследования: формулу длины окружности можно получить самостоятельно экспериментальным путем.
Основные понятия
Окружность — это замкнутая плоская кривая линия, все точки которой находятся на одинаковом расстоянии от заданной точки О. Эта точка называется центром окружности (рисунок 1,а).
Круг — часть плоскости, ограниченная окружностью (рисунок 1,б).
Можно сказать, что окружность является границей круга.
Основные линии окружности — радиус и диаметр (рисунок 1,а).
Радиус R окружности — это отрезок, соединяющий центр О с любой точкой окружности.
Диаметр D окружности — отрезок, который соединяет две точки окружности и проходит через ее центр.
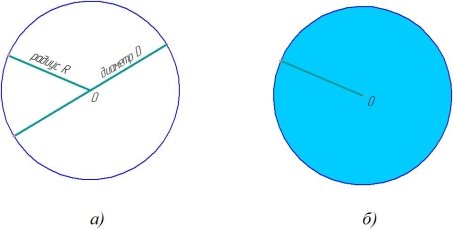
Рис. 1. Окружность и круг
Способы нахождения длины окружности
Рассмотрим некоторые возможные способы нахождения длины окружности.
Нахождение длины окружности с помощью нити
Когда я впервые задумался над решением данной задачи, первое и самое простое, что пришло на ум — это приложить нить к окружности, а затем при помощи линейки измерить ее длину. Подготовиться к эксперименту мне помог папа: он вырезал на станке металлические круги разных диаметров.
Проведем измерение круга диаметром 50 мм. Я обернул круг нитью, шариковой ручкой сделал отметки и при помощи линейки измерил длину нити между отметками (рисунок 2).
Длина нити оказалась равной 158 мм. При измерении я обратил внимание на то, что результат получается приблизительным, так как зависит от силы натяжения нити и ее толщины. И самое главное — не каждую окружность можно измерить таким способом.
То есть данный экспериментальный способ не решает поставленной задачи. Необходимо получить универсальную формулу, при помощи которой можно было бы найти длину окружности любого диаметра.



Рис. 2. Нахождение длины окружности с помощью нити
Нахождение длины окружности с помощью квадратов
Следующий способ, который я решил применить: представить окружность в виде квадрата (рисунок 3).
Продолжаем исследовать окружность диаметром 50 мм (рисунок 3,а).
Построим вокруг окружности квадрат так, чтобы он касался окружности в 4-х точках (рисунок 3,б), то есть сторона квадрата равна диаметру окружности.
Но на рисунке видно, что периметр квадрата явно больше длины вписанной окружности. А что, если внутри окружности построить еще один квадрат? Тогда, возможно, длина окружности будет средней величиной между периметрами двух квадратов.
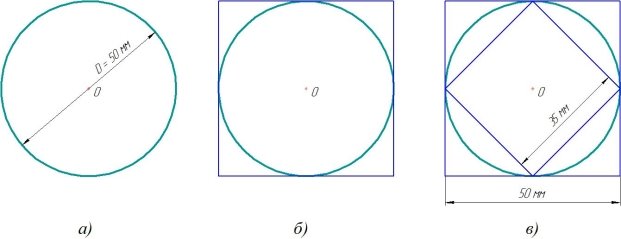
Рис. 3
Измерим длины сторон квадратов с помощью линейки (рисунок 3,в). Длина стороны внутреннего квадрата равна 35 мм, наружного — 50 мм.
Найдем периметры квадратов:
Периметр внутреннего квадрата Р внутр = 35+35+35+35 = 435= 140 (мм);
Периметр внешнего квадрата Р внешн = 50+50+50+50= 450 = 200 (мм).
Предположим, что длина окружности — это средняя величина двух периметров. Найдём, чему она равна: (140+200):2 = 170 (мм).
Это значение намного отличается от длины окружности, полученной при измерении с помощью нити — 158 мм, что говорит о невысокой точности этого метода.
Нахождение длины окружности с помощью многоугольников
Далее я предположил, что если внутри окружности построить многоугольник с большим количеством сторон, то его периметр будет больше приближен к длине описанной окружности.
Для того чтобы подтвердить своё предположение, я решил исследовать несколько геометрических фигур: шестиугольник, восьмиугольник, двенадцатиугольник. Диаметр окружности — 50 мм (рисунок 4).
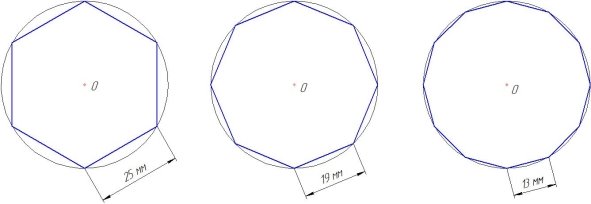
Рис. 4
Измерим линейкой длины сторон и с помощью калькулятора найдем периметры построенных фигур.
Периметр шестиугольника (обозначим его Р 6 ) равен:
Р 6 = 25+25+25+25+25+25= 625 = 150 (мм).
Найдем периметры восьмиугольника Р 8 и двенадцатиугольника Р 12 :
Р 8 = 19+19+19+19+19+19+19+19 = 819 = 152 (мм);
Р 12 = 13+13+13+13+13+13+13+13+13+13+13+13 = 1213 = 156 (мм).
Из полученных результатов можно сделать вывод, что чем больше сторон имеет многоугольник, тем больше его периметр будет приближен к реальной длине окружности, в которую он вписан.
Получение формулы длины окружности экспериментальным методом
От геометрических построений переходим к практическому исследованию и попробуем ответить на вопрос: существует ли связь между диаметром окружности и его длиной.
Экспериментальным способом найдём длины 3-х окружностей диаметром 50, 100 и 200 мм.
Для эксперимента нам понадобятся: 3 металлических круга диаметром 50, 100 и 200 мм, простой карандаш, цветные карандаши, лист ватмана, линейка, рулетка, корпус шариковой ручки, выполняющий роль оси вращения (рисунок 5).


Рис. 5. Подготовка к эксперименту
Для нахождения длины окружности мы будем катить металлический круг, как колесо, по прямой линии, проведенной на листе ватмана. На круге сделана насечка для того, чтобы можно было отметить, когда круг сделает полный оборот. Расстояние, которое пройдет круг за один оборот, и будет являться длиной окружности соответствующего диаметра (рисунок 6).


Рис. 6. Проведение эксперимента
В ходе эксперимента мы получили следующие результаты (рисунок 7).
Длина окружности, диаметр которой D 1 = 50мм, равна 157мм, то есть L 1 =157 мм.
Длина окружности диаметром D 2 =100 мм равна L 2 =314 мм.
Длина окружности диаметром D 3 =200 мм равна L 3 =628 мм.

Рис. 7. Результаты эксперимента
Представим полученные результаты в виде таблицы.
|
Диаметр окружности, мм |
50 |
100 |
200 |
|
Длина окружности, мм |
157 |
314 |
628 |
Сравним полученные результаты. Из таблицы видно, что при увеличении диаметра окружности в 2 раза, длина окружности увеличивается также в 2 раза. Отсюда можно сделать вывод, что отношение длины окружности к её диаметру — одинаковая величина для любой окружности, то есть:
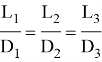
С помощью калькулятора выполним расчет:
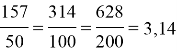
Экспериментальным методом мы определили, что отношение длины к диаметру окружности — постоянная величина, приблизительно равная 3,14.
Уже более 2 тыс. лет назад древнегреческий математик Архимед в своих научных трудах доказал, что отношение длины окружности к её диаметру является постоянной величиной, равной 3,14.
В 1706 году британский математик Уильям Джонс предложил это отношение обозначать греческой буквой
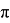
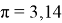
Зная отношение длины окружности к диаметру, получим формулу для нахождения длины окружности:
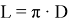
При помощи этой формулы можно вычислить длину любой окружности, насколько бы велика или мала она не была, или решить обратную задачу для нахождения радиуса окружности, если известна её длина.
Заключение
Таким образом, были исследованы различные способы нахождения длины окружности: с помощью нити, методом квадратов, с помощью многоугольников, в результате чего мы пришли к выводу, что метод многоугольников позволяет найти наиболее точное значение длины окружности.
Экспериментальным путем найдена взаимосвязь между диаметром окружности и её длиной и получена формула для нахождения длины окружности
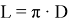
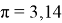
Литература:
- Энциклопедический словарь юного математика/Сост. А. П. Савин. — М.: Педагогика, 1989. — 352 с.: ил.
- Что такое. Кто такой: В 3 т. Т. 1–4-е изд., перераб. и доп. — М.: Педагогика-Пресс, 1998. — 384 с.: ил.
- Что такое. Кто такой: В 3 т. Т. 2–4-е изд., перераб. И доп. — М.: Педагогика-Пресс, 1998. — 416 с.: ил.
- Окружность: история // ВикипедиЯ. URL: https://ru.wikipedia.org/wiki/ %D0 %9E %D0 %BA %D1 %80 %D1 %83 %D0 %B6 %D0 %BD %D0 %BE %D1 %81 %D1 %82 %D1 %8C (дата обращения: 11.12.2019).

