Введение
Векторная арифметика — основа 3D графики, физики и анимации, и, для получения максимальной отдачи от Unity, весьма полезно досконально разбираться в этой теме. Однако, в курсе математики средней школы изучению вопросов векторной алгебры, по нашему мнению, уделяется недостаточно времени [1]. Желание понимать принципы работы Unity с позиций векторной алгебры, как средства разработки компьютерных игр, мотивировало автора на более подробное изучение соответствующих разделов линейной и векторной алгебры.
Цель работы: выявление сущности создания компьютерных игр на базе использования понятий линейной и векторной алгебр и практическая реализация компьютерной игры на основе теории векторов.
Достижение поставленной цели требует решения следующих задач:
- Рассмотреть современные тенденции игростроения.
- Изучить понятийный аппарат линейной алгебры, необходимый для работы с движком Unity.
- Организовать эффектный и стабильный процесс разработки игр на основе интеграции линейной и векторной алгебр и функционала движка Unity.
Основная часть
В качестве инструмента создания компьютерной игры, которую автор назвала CarSchool, был выбран игровой движок Unity. Такой выбор обусловлен простотой его использования и функциональностью [2].
Разработка проекта компьютерной игры в Unity сводится к созданию сцен, на которых, размещаются объекты, необходимые в тот или иной момент игры. К каждому такому объекту есть возможность подключать компоненты, определяющие его характеристики и поведение. Unity в своём арсенале уже имеет определенное количество компонентов, обеспечивающих, в том числе, физику внутри игры и отображение объектов, но, несмотря на это, создатели Unity предоставили возможность разработчикам самим переопределять и создавать новые компоненты, реализуя их на языках программирования, например, таких как C# и Java. Такая возможность самостоятельно доопределять новые компоненты игры, является для начинающего разработчика хорошей мотивацией на изучение этих языков программирования.
Игровой движок (Game Engine) обеспечивает основную функциональность системы Unity 3D. Он включает в себя многократно используемые программные компоненты: графический движок («визуализатор»), физический движок, звуковой движок, систему скриптов, анимацию, искусственный интеллект, сетевой код, и управление памятью [3–6].
Одним из основных преимуществ использования Unity является его кроссплатформенность. На сегодняшний день Unity поддерживает 29 платформ, среди которых: iOS, Android, Windows, macOS, PlayStation VR, Samsung Smart TV и др. Из этого списка видно, что поддерживаются не только мобильные устройства, консоли и браузеры, но и умные телевизоры, и шлемы виртуальной реальности.
Разработка компьютерной игры строится по принципу «компьютерной инженерной лаборатории» (КИЛ)[1], поэтому обладает возможностями исследования модели с изменением её параметров. КИЛ предназначена для исследования динамических моделей технических систем на основе их математических моделей. Система КИЛ строится таким образом, чтобы пользователь имел возможность экспериментировать с моделью, при этом активно воздействовать на предлагаемый алгоритм решения задачи.
При проектировании визуальной модели эти функции группируются в сценарии, по которым строятся основные алгоритмы реализации модели. Другими словами, когда игра запущена, компьютер всё рассчитывает с огромной скоростью, — в единицу времени производится множество операций. Это значит, что пока мы видим плавно передвигающийся объект по сцене, компьютер вычисляет множество параметров: скорость, направление, местоположение объекта с помощью нескольких векторов. При этом используются такие понятия линейной алгебры, как сложение векторов, разность векторов, умножение вектора на число, определение расстояния между точками в трёхмерном пространстве, скалярное и векторное произведения. В процессе игры пользователь может менять многие параметры объектов, а компьютер «незаметно» для пользователя делает перерасчёт новых данных.
Структура программного комплекса игры представлена тремя блоками: «Создание 3D всех объектов игры с использование элементов линейной алгебры», «Моделирование движения объектов», «Компиляция игры на платформу Windows» (рис. 1).
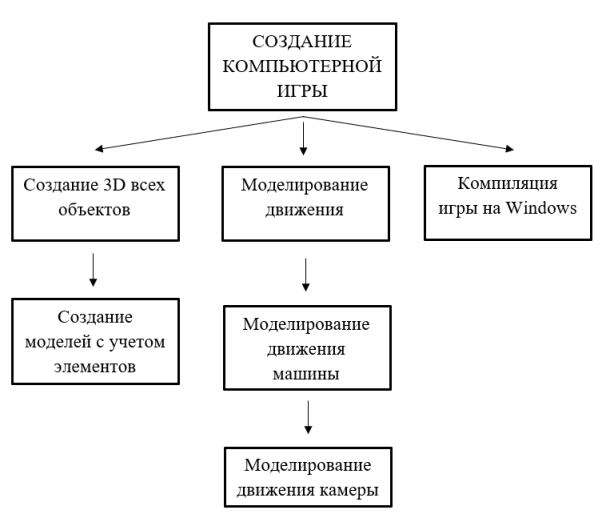
Рис. 1. Структурная схема создания компьютерной игры
На начальном этапе работы необходимо было продумать все модели, объекты, которые будут использоваться в игре. Создать визуальный образ программы.
Все модели в компьютерной игре состоят из векторов, и путём их сложения, умножения, вычитания строятся полноценные объекты (рис. 2). Поэтому для того чтобы создать сами модели, мы использовали понятия вектора, длины вектора, равенство векторов, умножение вектора на число, сложение и вычитание векторов, скалярное и векторное произведения и другие понятия линейной алгебры. Таким образом, для написания качественной компьютерной игры, необходимы хорошие знания векторной алгебры.
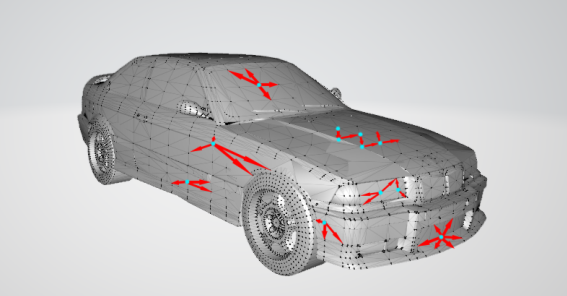
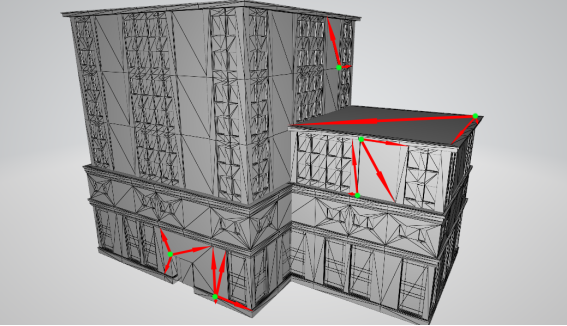
Рис. 2. Модели, состоящие из векторов
В Unity вектора используются для хранения местоположений объектов, направления их движения и скоростей, поэтому углубляясь в детализацию разработки программы игры рассмотрим последовательно свойства векторов и операций над ними по отдельности [7].
Известно, что вектор, как геометрическое понятие, характеризуется тремя величинами: точкой приложения, величиной (модулем или длиной) и направлением в пространстве [8]. Для работы с векторами в трёхмерном пространстве есть несколько полезных функций Unity.
Рассматривая вектор как вектор, определяющий местоположение объекта, приходим к выводу, что с его помощью можно определить на каком расстоянии (используя расстояние между точками) машина (игрок) находится от объекта. Это необходимо, например, чтобы понимать, как далеко находится преграда (рис. 3).

Рис. 3. Местоположение
При использовании вектора Unity в качестве вектора скорости движения, мы будем указывать скорость движения объекта на конкретный момент времени («мгновенная» скорость). Это помогает понять, как быстро разгоняется машина, то есть игрок оценивает её характеристики и рассчитывает траекторию движения. На рисунке 4 показана скорость, рассчитанная с помощью векторов скорости (с использованием операций над векторами, рассмотренные ниже).

Рис.4. Скорость движения
Рассматривая вектор, как направление, мы получаем направление движения объекта. С помощью этого вектора игрок выбирает, в каком направлении двигаться, чтобы одержать победу в игре (рис. 5).
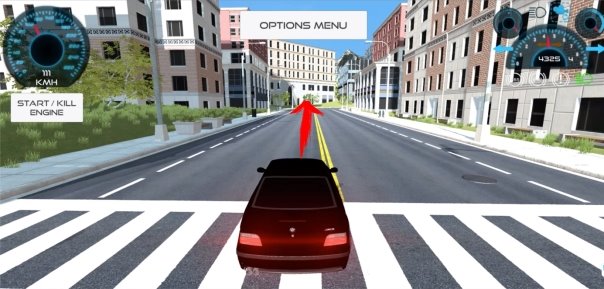

Рис. 5. Направление движения
При складывании (вычитании) векторов определяется текущее местоположение объекта, его скорость на данный момент времени и направление. Все эти данные необходимы, чтобы пользователь мог полноценно управлять игрой.
Умножение вектора на скаляр — это изменение местоположения, скорости, направления объекта в каждом кадре. При создании гоночной игры это обязательно следует учитывать. В любой момент времени машина может увеличить скорость в несколько раз. Компьютер с помощью данных о местоположении, скорости и направлении движения машины рассчитывает новую скорость, в разы большую предыдущего значения. Математические действия производятся путем умножения вектора на скаляр.
Для нахождения скалярного произведения двух векторов, находим сумму произведений соответствующих координат векторов:
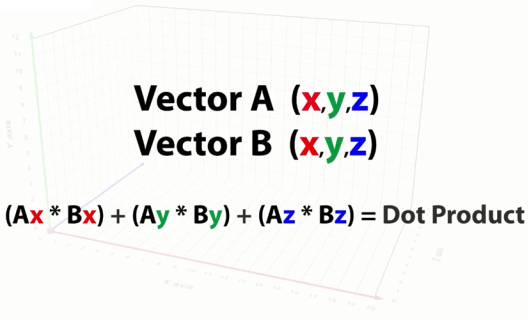
Рис. 6. Скалярное произведение двух векторов
При помощи скалярного произведения узнаём дополнительную информацию о векторах. Например, перпендикулярны они или нет? Если скалярное произведение двух векторов равно нулю, значит, векторы перпендикулярны. В Unity есть вспомогательная функция для расчёта скалярного произведения векторов Vector3.Dot(VectorA,VectorB).
Векторное произведение. Вместо вычисления скаляра векторное произведение даёт другой вектор, перпендикулярный двум исходным. Например, если векторное произведение векторов a и b будет равняться вектору c, то он будет перпендикулярен a и b. Направление векторов, при этом, определяется по правилу левой руки.
Для математического расчёта векторного произведения необходимо записать координаты векторов a и b в виде матриц.
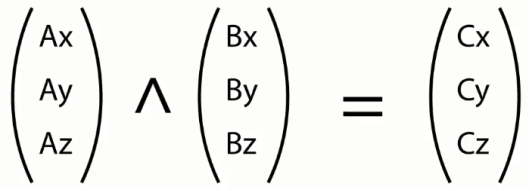
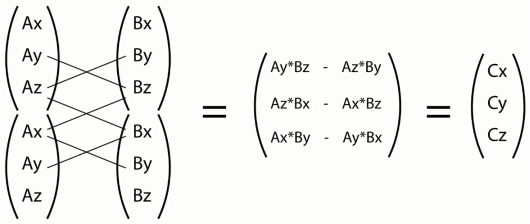
Рис. 7. Векторное произведение двух векторов
Для упрощения подобных расчётов в Unity есть вспомогательная функция Vector3.Cross(VectorA,VectorB).
Еще одно понятие линейной алгебры — расстояние между точками. В нашей игре это необходимо, чтобы рассчитывать, например, на какое расстояние должен подойти объект (персонаж), чтобы оказаться в машине. Как только персонаж попадает в радиус-вектор захвата машины, он оказывается внутри неё. А значит нужно выяснить, какое расстояние ему ещё необходимо пройти. Так же, какой еще путь по прямой осталось проехать машине, чтобы оказаться на финише, всё это рассчитывается компьютером и важно в создании игр. Unity упрощает выполнение подобных расчётов при помощи функции Vector3.Magnitude.
На основании вышеизложенного можно сделать вывод, что игра построена на векторах, векторы изменяются путём математических преобразований и в результате, собственно, и получается сам процесс игры. Разработчик игр, владея базовыми знаниями линейной алгебры способен более точными, ясными и практичными путями создавать качественные компьютерные игры.
Поведение объектов контролируется с помощью компонентов (Components), которые присоединяются к ним. Помимо множества встроенных в Unity стандартных компонентов, игровой движок позволяет создавать свои компоненты, используя аппарат скриптов. Они, в свою очередь, позволяют активировать динамические события, изменять параметры компонентов, а также вести диалог с пользователем в интерактивном режиме реального времени, реагируя на ввод новых параметров модели.
При помощи скриптов, разработанных на языках программирования C# или Java, можно реализовать следующие алгоритмы:
− алгоритм движения машины по результатам решения определенных задач (например, путём решения системы дифференциальных уравнений n-го порядка);
− алгоритм движения графического объекта по поверхности с определёнными характеристиками (коэффициент сцепления) с заданной скоростью;
− алгоритм движения и управления камерой (создаётся с применением матриц);
− алгоритм сканирования неровности опорной поверхности;
− алгоритм построения графика согласно полученным результатам решения определенных задач (решение дифференциальных уравнений);
− алгоритм динамического изменения опорной поверхности;
− алгоритм запуска игры.
В перечисленном автор видит направления дальнейшего развития алгоритма игры. Итог настоящей работы — это созданная автором игра на движке Unity, скомпилированная на платформе Windows.
Заключение
Создание игр кажется чем-то увлекательным и для многих стало причиной начать программировать, однако разработка игр требует от разработчика хороших знаний математики. Чтобы создать эффективную и практичную игру, программисту нужно знать основы линейной и векторной алгебр, а также уметь применять их на практике. Математикой в играх может оказаться сложение векторов, их разность, манипулирование косинусами, синусами, в продвинутых играх необходимо применять математические навыки, чтобы результат был достойный и качественный.
Компании, занимающиеся разработкой игр, требуют от своих сотрудников знания математики и алгоритмов. Знание таких вещей не просто помогает разработать логику игры, но и качественно оптимизировать саму игру, находя альтернативные пути, которые позволяют избежать лишних вычислений.
Векторы и векторная математика являются необходимыми инструментами для разработки игр. Многие операции и действия завязаны на ней целиком. Например, для реализации класса, который отображает стрелочку вектора в Unity3D, уже требует знания большинства типовых математических операций.
В своей научно-исследовательской работе мы показали только часть приложений векторной алгебры для создания игр.
Практическим результатом теоретического изучения элементов линейной алгебры явилась разработка компьютерной игры на движке Unity. Создан алгоритм (выбор математической модели, создание компьютерной модели на базе математической модели, визуализация результатов моделирования в графическом виде, 3D-моделирование динамической системы в реальном времени) модели объектов игры, которые обладают следующими возможностями:
− получение функции перемещение объекта в численном и графическом виде;
− визуальное отображение движения объекта;
− исследование влияния внутренних параметров объекта (например, жёсткость пружины или масса) на экстремальные значения выходных параметров в динамическом режиме;
− исследование влияния входных воздействий на экстремальные значения выходных параметров в динамическом режиме.
Апробация игры проводилась одноклассниками моей гимназии. Ребята в целом остались довольны игрой и выразили пожелания на дальнейшее её развитие и совершенствование функционала, которые автор обязательно будет учитывать.

Рис. 8. Апробация игры
Перспективы развития настоящей работы вижу следующие. В дальнейшем планирую совершенствовать разработанную игру. Развитие алгоритма компьютерной игры должно идти в направлении разработки разных по сложности уровней с возможностью выбора конфигурации трасс, разных моделей автомобилей с различающимися динамическими характеристиками, количества участников игры, с возможностью выхода в сеть и организации командных турниров.
Литература:
- Геометрия. 7–9 классы: учебник для общеобразовательных учреждений / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. — 20-е изд. — М.: Просвещение, 2010. — 384 с.
- Х-обзор: сравниваем топ-6 лучших игровых движков для программиста. [Электронный ресурс]. Режим доступа: https://xakep.ru/2016/10/17/top6-game-engines/
- Торн А. «Основы анимации в Unity». — М.: «ДМК Пресс», 2016. — 176 с.
- Unity (игровой движок). [Электронный ресурс]. https://ru.wikipedia.org/wiki/Unity_(игровой_движок)
- Unity — Unity Personal. [Электронный ресурс]. Режим доступа: https://store.unity.com/ru/products/unity-personal?_ga=2.50651498.25483083.1551193591–1522839189.1546778152
- Unity — Руководство. [Электронный ресурс]. Режим доступа: https://docs.unity3d.com/ru/530/Manual/UnityManual.html
- «Математика для программирования 3D игр и компьютерной графики», Эрик. Ленгиель. 2011. (Mathematics for 3D Game Programming and Computer Graphics, Third Edition 3rd Edition, E. Lengyel).
- Вектор. [Электронный ресурс]. https://ru.wikipedia.org/wiki/Вектор_(геометрия)
[1] Компьютерная инженерия - дисциплина, которая объединяет информатику и электронную инженерию. Эта область инженерии сосредоточена не только на самой работе компьютерных систем, но и на их интеграции. В её лабораториях проводится анализ и разработка всех программ.

