Ключевые слова: оптическая геометрия образования теней, уникальный теневой коэффициент каждой планеты, математические размеры источника сферического тела.
Прямолинейностью распространения световых лучей в оптической среде, отличным масштабом от квантового мира, объясняется образование полной тени и полутеней на экране от непрозрачного препятствия.
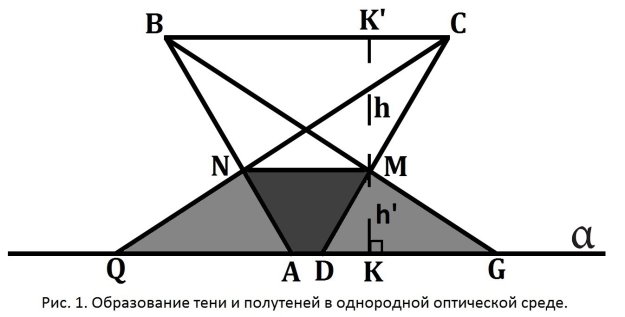
На (Рис. 1.): 1) BC-длина источника света 2) NM-длина препятствия для лучей света 3) Прямые BNA и CMD являются лучами света, которые касаются препятствия в точках N и M, и продолжаются до точек A и D на экране соответственно. В зону между точками A и D свет не попадает и образуется полная тень 4) Прямые BMG и CNQ являются лучами света, которые касаются препятствия в точках M и N, и продолжаются до точек G и Q на экране соответственно. В зоны QA и DG свет падает частично и образуются полутени 5) 
-расстояние от экрана до препятствия (наикратчайшее расстояние-перпендикуляр) 6) h-расстояние от препятствия до источника света (перпендикуляр) 7) 
-экран.
Экран (плоскость
), препятствие (NM) и источник света (BC) параллельны друг другу.
Геометрия образования полной тени и полутеней.
1) Геометрия образования полной тени.
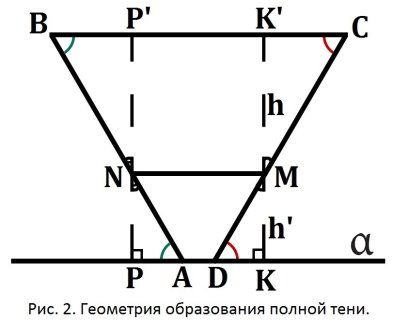
Рассмотрим первым делом геометрию образования полной тени. Для этого рассмотрим трапецию ABCD (Рис. 2.). Проведем дополнительные построения: 1) Перпендикуляр 
, проходящий через точку M 2) Перпендикуляр 
, проходящий через точку N.
Из подобия треугольников 
и 
следует, что отношение высот 
есть показатель коэффициента подобия этих треугольников (k). Значит их стороны будут относится друг к другу на величину коэффициента подобия = k.
(1)
Выразим длину полной тени на экране, выражая через разбиения образованные на экране.
PK=NM, поскольку образованы соответственно параллельными сторонами.
Подставами вместо суммы PA+DK то что мы получили в (1)
(2)
Найдем длину источника света, складывая разбиения образованные в результате опускания перпендикуляров.
Выразим из этого равенства сумму 
, чтобы подставить в (2) и избавится от лишних неизвестных.
равно NM, поскольку они так же образованы перпендикулярами опушенными из параллельных сторон.
Подставим это значение в (2).
(3)
Данное равенство объясняет геометрию образования только полной тени.
2) Геометрия образования полутеней.
Теперь рассмотрим геометрию образования полутеней, чтобы затем сложить их значение со значением полной тени, и таким образом вывести формулу для нахождения длины всей тени.
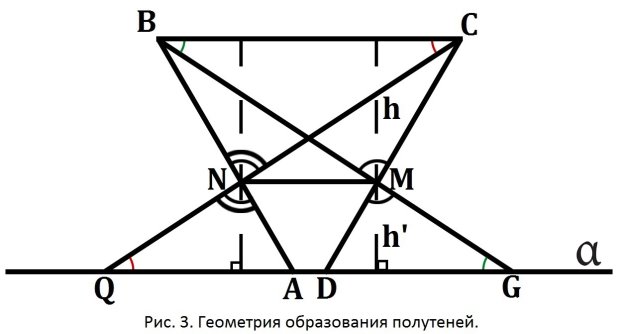
На (Рис. 3.) QA и DG — полутени, образованные от источника света BC.
(4)
Теперь сложим значения полной тени и полутеней, чтобы найти длину всей тени. То есть сложим (3) и (4).
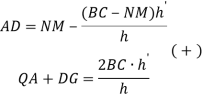
Дадим геометрическим величинам физические обозначения:
По данной формуле практично подсчитывать геометрию образования теней на небольших расстояниях (при Земных условиях). Таким образом, мы получили уравнение, связывающее длину тени на экране со всеми переменными, которые могут повлиять на ее конечное значение.
В действительности все источники имеют некоторые размеры. Однако для решения некоторых теоретических задач может потребоваться формула для описания образования теней от точечного источника света. Итак, образование тени от точечного источника, будет определяться как предел функции основной формулы образования теней (уравнении-1), где размер источника будет стремиться к нулю.
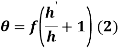
Если источник света точечный, то на экране полутени полностью отсутствуют и наблюдается только полная тень с очень четкими краями.
Применение в Астрономии. И следствия, вытекающие из поставленных задач.
Данная геометрия теней так же применима на намного больших расстояниях (при Астрономических расчетах), поскольку образование теней на поверхности планет от освещения звезд, является следствием все той же геометрии.
Перепишем основную формулу образования теней следующим образом:
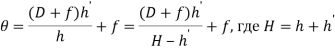
После некоторых преобразований имеем:
В приближении можно принять 
, где 
-расстояние от математической длины источника света до поверхности планеты, 
-радиус орбиты данной планеты.
Заметим, что в знаменателе дроби значение
пренебрежительно мало по сравнению с , поэтому:
Теперь можно заметить, что для каждой планеты значение отношения диаметра звезды 
в системе с которой находится данная планета к радиусу орбиты данной планеты 
, будет постоянной физической величиной. Обозначим отношение 
через 
, и дадим ему физический смысл уникального теневого коэффициента пропорциональности для каждой планеты 
.
Где — уникальный теневой коэффициент для данной планеты, заранее который можно подсчитать для любой планеты по формуле 
.
Поскольку в контексте Астрономических масштабов размеры источников (Звезд) всегда будут больше препятствий, то следствием данной геометрии теней становится то, что при повышении высоты предмета над поверхностью планеты наступит момент, при котором полная тень полностью исчезнет над поверхностью планеты и останутся только очень размытые и незаметные элементы полутеней (создается иллюзия, что тень от предмета полностью исчезла). Следовательно, при достижении телом данной высоты, дальнейшие подсчеты по (уравнение-3) становятся бессмысленными.
Отталкиваясь от основной формулы образования только полной тени (равенство-3), можно вывести формулу подсчета минимальной высоты, на которое необходимо поднять тело, чтобы тень от него полностью исчезла над поверхностью планеты.
Заменив в (равенство-3) геометрические обозначения физическими величинами и выразив значение , имеем:
Чем меньше будет длина тени, тем ближе значение 
будет приближаться к своему значению, при котором тень полностью исчезнет. Следовательно, значение при котором тень полностью исчезнет над поверхностью планеты, будет определяться как предел функции где длина полной тени будет стремиться к нулю.
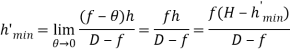
После нетрудных преобразований, имеем:
Значение минимальной высоты на которое необходимо поднять тело, что бы тень от него полностью исчезла на поверхности данной планеты, прямо-пропорционально размерам препятствия, где 
— обратная величина уникального теневого коэффициента для данной планеты.
Отсутствие теней на поверхности Земли от электрических проводов на большой высоте и многие другие иллюзии отсутствия теней объясняется этой формулой.
2) Следствия, вытекающие из поставленных задач.
При попытке переноса уравнений в Астрономические масштабы, была замечена одна очень важная особенность математического значения длины источника сферических тел (Звезд). Эта особенность говорит о том, что на самом деле математические размеры источников сферических тел не равны длине их диаметра, а равны некоторой хорде для данной окружности сферического тела. Данная особенность следует из того, что две касательные, проведенные к окружности из одной точки, не могут достигать диаметра данной окружности.
Предположим, что наблюдатель находится в точке A и его взгляд направлен на сферическое тело с центром в точке O (Рис. 4). Тогда касательные, проведенные из точки A к окружности, будут соединять наблюдателя с самыми крайними точками сферы, которые может увидеть наблюдатель, находящийся в точке A, прежде чем его взгляд уйдет в бесконечность. Соединив точки соприкосновения касательных с окружностью B и C, мы получим видимую математическую длину хорды сферического тела BC. Следовательно, при взгляде на сферическое тело мы видим его двумерное изображение не в плоскости диаметра, а в плоскости некоторой хорды, образованной от касательных, проведенных к окружности из точки наблюдения.
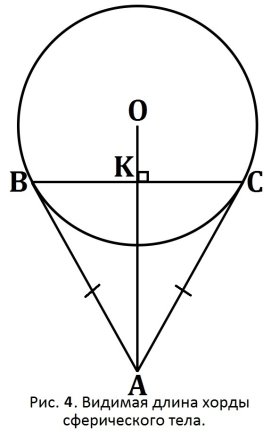
Из свойств касательных, следует что две касательные, проведенные из одной точки к окружности равны AB=AC 
-равнобедренный. Так же из свойств касательных проведенных к окружности из одной точки следует, что биссектриса, исходящая из высоты треугольника, проходит через центр окружности (под биссектрисой подразумевается линия наблюдателя). Но поскольку 
-равнобедренный, то линии биссектрисы, медианы и высоты будут совпадать. То есть AK-так же высота
. Таким образом плоскость видимой длины хорды сферического тела всегда перпендикулярна к линии наблюдателя, смотрящего на данное сферическое тело.
Из сделанных умозаключений можно прийти еще и ко второму выводу: если некоторое сферическое тело является источником света, то математическая длина источника будет не диаметр сферы, а некоторая хорда, образованная от проведения касательных к окружности.
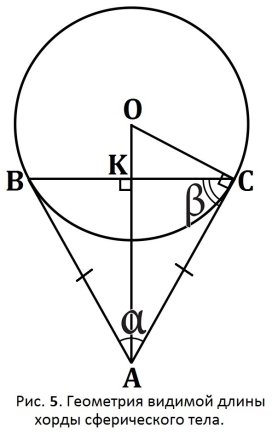
Выведем формулу для нахождения видимой длины хорды сферического тела из произвольной точки наблюдения.
Рассмотрим на (Рис. 5.) 
–равнобедренный. Углы при основании равнобедренного треугольника равны
Радиус и касательная к данной точке окружности, образуют прямой угол. Следовательно, угол 
вычисляется так:
Линия AK так же является медианой, опущенной из вершины 
на сторону BC (так как -равнобедренный)
BK=KC, тогда из треугольника 
тригонометрическим тождеством найдем катет CK, который будет половиной видимой длины хорды сферического тела BC.
Где 
— видимая длина хорды сферического тела из точки наблюдения, 
-действительный диаметр сферического тела, 
-видимый угловой диаметр сферического тела из точки наблюдения.
Для очень далеких объектов значение видимой длины хорды сферического тела будет очень близка к действительному значению диаметра его сферы. Это происходит потому, что чем дальше находится тело от точки наблюдения, тем меньше становится его видимый угловой диаметр на небесной сфере, следовательно, значение угла 
будет стремиться к нулю, соответственно функция косинуса будет стремиться к единице. Подсчеты по формуле (уравнение-5) дают значение видимой длины хорды Солнечной сферы наблюдаемого с Земли равным 1.391.385 км, при действительном значении диаметра Солнца равным 1.391.400 км и видимом угловом диаметре с Земли равным 
. Как и ожидалось значение видимой длины хорды Солнца очень близко к действительному значению диаметра (разница всего в 15 км).
Таким образом, логичным будет теперь уточнить что термин «видимый угловой диаметр» сферического тела не совсем верно сформулирован. Поскольку в действительности наблюдатель и любые угловые измерительные устройства не могут видеть любое сферическое тело в его угловом диаметре (поскольку не могут увидеть его вдоль диаметра). В действительности наблюдатель может только измерить угол, под которым он видит сферическое тело вдоль ее видимой хорды. То есть правильнее говорить «видимая угловая хорда».
Для окончательного доказательства этого предположения мы можем вывести формулу, основываясь на этом представлении, для нахождения размеров планет, звезд и т. д., зная расстояние до них и их видимую угловую хорду. И если проведенные подсчеты по этой формуле согласуются с известными значениями размеров небесных тел, то можно будет без сомнений убедиться в правдивости этого предположения.
Рассмотрим прямоугольный треугольник 
(Рис. 5.):
По формуле для равнобедренного треугольника основание треугольника BC вычисляется по формуле:
Прировняем это равенство с 
(уравнение-5), но прежде представим действительный диаметр как удвоенный радиус 
Представим 
как квадрат косинуса половинного угла 
и раскроем скобки в правой части равенства
Таким образом, мы вывели уравнение для нахождения радиуса небесных тел, зная расстояние до них и их видимую угловую хорду. Теперь, к примеру, если подсчитать размеры Луны, то подсчеты, проведенные по этой формуле, дают значение радиуса Луны равным 1.737 км, при расстоянии до Луны 384.400 км и видимой угловой хорде 
. То есть значение получается в точности равным действительному. Итак, согласование подсчетов проведенных по этой формуле с действительными значениями небесных тел, является основным доводом в пользу доказательства правдивости предположения о видимой длине хорды сферических тел. Однако это предположение так же не противоречит астрономическим подсчетам, к примеру по формуле 
, поскольку касательная и радиус к данной точке окружности всегда образуют прямой угол и тригонометрическое тождество в прямоугольном треугольнике всегда будет оставаться действительным.
Заключение
В работе была показана предсказуемость геометрии образования теней на различных планетах, связав соответствующие уравнения с уникальным теневыми коэффициентами данных планет. Пользуясь данными уравнения можно предсказывать геометрию теней на любой планете, без проведения на них каких-либо предварительных измерительных опытов, а просто изначально посчитав для необходимой планеты ее уникальный теневой коэффициент.
Ниже приведена таблица значений уникальных теневых коэффициентов для планет нашей Солнечной системы, с точностью до трех знаков после запятой:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Было сделано предположение, что при взгляде на сферическое тело, наблюдатель видит его не в диаметре, а вдоль некоторой хорды. Была выведена формула для нахождения длины данной видимой хорды сферического тела, которая так же является математической длиной источника света для места проведения измерений. Дальнейшие согласования по выведенной формуле с известными значениями размеров небесных тел, стали основным доказательством данного предположения.
