Мысль выражать все числа немногими знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна.
Пьер-Симон Лаплас (1749–1827)
Десятичная система счисления, которой мы пользуемся, кажется нам единственно удобной и пригодной для вычислений. Но так ли это? Попробуем выяснить какие системы счисления существуют, и какое применение находят различные системы счисления в практической деятельности человека.
Система счисления — способ изображения чисел при помощи ограниченного набора символов (цифр), и правила выполнения действий над этими числами.
Различают позиционные и непозиционные системы. В непозиционной системе счисления значение цифры не зависит от её положения в записи числа. Примером непозиционной системы счисления, достаточно широко применяющейся в наше время, может служить так называемая римская нумерация (римская система, римские цифры), в которой для записи чисел используют лишь семь цифр I − 1, V − 5, X − 10, L − 50, C − 100, D −500, M — 1000. С помощью этих цифр можно записать любое число, используя принцип прибавления и вычитания. Отнимать можно, как правило, не больше одного знака, а прибавлять не больше трех одинаковых знаков. Знак, стоящий слева от другого знака, уменьшает значение старшего знака. Знак, стоящий справа от другого (старшего) знака, увеличивает значение старшего знака. Например, запись римскими цифрами числа 88: LXXXVIII.
Записи даже не очень больших чисел в римской нумерации длинные, умножение и деление письменно выполнять практически невозможно. Даже для того, чтобы прочитать число нужно сначала выполнить действия сложения и вычитания устно. Именно поэтому римская система счисления в математике практически не применяется. Римские цифры используются редко, в основном в хронологии для нумерации столетий, для нумерации разделов книг, иногда они встречаются на циферблатах часов и т. д.
Общие недостатки всех непозиционных систем:
– существует постоянная потребность введения новых знаков для записи больших чисел;
– невозможно представлять дробные и отрицательные числа.
– сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения.
В позиционных системах счисления знаки, с помощью которых записываются числа называются цифрами, всё множество используемых знаков (цифр) − алфавитом, а их количество в алфавите − основанием системы счисления. Значение каждой цифры меняется в зависимости от её положения (позиции) в последовательности цифр, изображающих число.
Достоинства позиционных систем
– простота выполнения арифметических операций;
– ограниченное количество символов, необходимых для записи любого числа;
– удобство для механического представления чисел.
Первой известной нам системой счисления была шестидесятеричная система вавилонян, возникшая примерно за 2200–2000 лет до н. э. Вавилоняне записывали все числа от 1 до 59 по десятичной системе, применяя принцип сложения и используя всего два знака − вертикальный и горизонтальный клинья. Их получали при надавливании по сырой глиняной дощечке острием треугольной палочки. Счёт в пределах разрядов они вели по десятичной системе, а при переходе от одного разряда к другому − по шестидесятеричной. Однако у шумеро-вавилонских математиков не было знака нуля, а когда он появился, его ставили лишь при отсутствии разрядов внутри числа и никогда не писали в конце числа. Поэтому записи чисел 12, 120, 1200 и т. д. ничем не отличались. Их можно было определить только из условия задачи или каким-либо другим способом. Поэтому вавилонская система счисления считается позиционной, но непоследовательной. Мы и сейчас пользуемся этой системой при измерении времени и углов.
В V-XII веках н. э. на полуострове Юкатан (Центральная Америка) племена индейцев майя создали двадцатеричную систему счисления (позиционную). В ней использовались три знака: единицы обозначались точками, пятерки − горизонтальными чертами и нуль — в форме ракушки. Однако бесценные творения удивительной культуры майя уничтожили огнем и мечом испанские конкистадоры.
Некогда у разных народов получила распространение двенадцатеричная система счисления. До сих пор мы делим год на 12 месяцев, сутки на ![]() часа (день и ночь). Согласно некоторым традициям и правилам этикета предметы интерьера (стулья), посуда и столовые приборы (тарелки, ножи, ложки) считают не десятками, а дюжинами (по 12 штук).
часа (день и ночь). Согласно некоторым традициям и правилам этикета предметы интерьера (стулья), посуда и столовые приборы (тарелки, ножи, ложки) считают не десятками, а дюжинами (по 12 штук).
Двоичную систему счисления, возможно, как самую простую, использовали на определённом этапе все народы. Считают, что она была изобретена в IV тысячелетии до н. э. Она фактически заменила иероглифическую позиционную систему счисления египтян.
Различают анатомические (десятичная, пятеричная, двенадцатеричная, двадцатеричная) и машинные (двоичная, восьмеричная, десятичная, шестнадцатеричная) системы счисления.
Жизнь в современном мире невозможно представить без компьютеров. Для того чтобы оценить пригодность той или иной системы счисления в качестве основы для конструирования ЭВМ, нужно учитывать два главных фактора: простота осуществления математических операций и экономичность системы. Экономичность системы определяется тем количеством чисел, которые можно записать в данной системе с помощью определенного числа знаков.
Например, давайте сравним десятичную и двоичную системы счисления. Для того, чтобы в десятичной системе записать 1000 чисел (от 0 до 999), необходимо 30 знаков (3 разряда, по 10 цифр для каждого разряда). А в двоичной системе с помощью 30 знаков можно записать ![]() различных чисел. Для каждого двоичного разряда нужны только две цифры − 0 и 1. Очевидно, что
различных чисел. Для каждого двоичного разряда нужны только две цифры − 0 и 1. Очевидно, что ![]() , поэтому имея всего 15 двоичных разрядов, можно записать гораздо больше различных чисел, при чем 3-х разрядных десятичных. Таким образом мы убедились, что двоичная система счисления выгоднее, а значит экономичнее, чем десятичная система.
, поэтому имея всего 15 двоичных разрядов, можно записать гораздо больше различных чисел, при чем 3-х разрядных десятичных. Таким образом мы убедились, что двоичная система счисления выгоднее, а значит экономичнее, чем десятичная система.
Какая же система счисления самая экономичная? Пусть в нашем распоряжении имеется ![]() знаков для записи чисел. Если за основание системы счисления взять некоторое число
знаков для записи чисел. Если за основание системы счисления взять некоторое число ![]() , то получится
, то получится ![]() разрядов числа. Тогда количество чисел, которые при этом можно составить, будет равно
разрядов числа. Тогда количество чисел, которые при этом можно составить, будет равно ![]() .
.
Рассмотрим полученное выражение как функцию от переменной ![]() , принимающей любые положительные значения (целые, дробные, иррациональные).
, принимающей любые положительные значения (целые, дробные, иррациональные). ![]() . Тогда задача будет формулироваться следующим образом: найти значение переменной
. Тогда задача будет формулироваться следующим образом: найти значение переменной ![]() , при котором эта функция достигает максимума.
, при котором эта функция достигает максимума.
Необходимое условие того, что в данной точке ![]() функция
функция ![]() достигает максимума, состоит в обращении в нуль её первой производной в этой точке. В нашем случае:
достигает максимума, состоит в обращении в нуль её первой производной в этой точке. В нашем случае: ![]() — показательно-степенная функция. Для нахождения производной этой функции мы применим логарифмическое дифференцирование.
— показательно-степенная функция. Для нахождения производной этой функции мы применим логарифмическое дифференцирование.
![]() ,
,
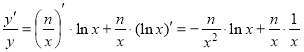 ,
,
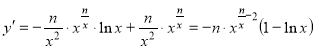 ,
,
![]()
![]() ,
, ![]() ,
,
где е − иррациональное число, которое является основанием натуральной системы логарифмов. е =2,7182818284599045…
Ближайшим к e целым числом является 3. Это число и будет основанием наиболее экономичной системы счисления. Применение троичной системы счисления влечет за собой конструктивные трудности применительно к ЭВМ (при этом нужно пользоваться элементами, каждый из которых может находиться не в двух, а в трех устойчивых состояниях). Поэтому приоритет относительно применения в ЭВМ пока что остается за двоичной системой счисления.
Наряду с изучением давно известных систем ученые разрабатывают альтернативные системы счисления, у которых алфавит и основание ![]() не обязательно натуральные числа, они могут быть целыми отрицательными или комплексными числами. Рассмотрим несколько примеров таких систем счисления.
не обязательно натуральные числа, они могут быть целыми отрицательными или комплексными числами. Рассмотрим несколько примеров таких систем счисления.
Уравновешенная троичная система счисления. Такую систему называют еще системой с симметричным основанием. Это система с основанием ![]() , но вместо традиционных цифр 0, 1, 2 в ней в качестве базисных используют цифры 1, 0,
, но вместо традиционных цифр 0, 1, 2 в ней в качестве базисных используют цифры 1, 0, ![]() , где
, где ![]() .
.
Примеры записи чисел в такой системе:
![]() ,
,
![]() .
.
Особенности этой системы:
– если число, записанное в уравновешенной системе, начинается цифрой ![]() , то оно отрицательное, а если цифрой 1, то оно положительное;
, то оно отрицательное, а если цифрой 1, то оно положительное;
– при выполнении арифметических действий над числами не требуется использовать правила знаков.
Нега-позиционная система счисления. Это система с целым отрицательным основанием. Если ![]() то система называется нега-двоичной; если
то система называется нега-двоичной; если ![]() − нега-четверичной и т. д.
− нега-четверичной и т. д.
Формула числа в такой системе:
![]()
![]()
![]()
![]()
Основным достоинством нега-позиционных систем с любым основанием является отсутствие знака перед отрицательными числами, а, следовательно, и отсутствие правила знаков.
Системы счисления с основанием, содержащим мнимую единицу ![]() . Из таких оснований больше всего для реализации на ЭВМ подходит основание
. Из таких оснований больше всего для реализации на ЭВМ подходит основание ![]() . Такая система называется мнимо-четверичная. Формула числа в ней записывается так:
. Такая система называется мнимо-четверичная. Формула числа в ней записывается так:
![]() , где
, где ![]() ,
, ![]() .
.
Пример:
![]() .
.
Оказывается, что очень легко осуществляется переход от мнимо-четверичной системы к десятичному комплексному числу и к нега-четверичной системе по формулам:
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.
Достоинство записи комплексного числа в цифровой форме: арифметические действия над числами, записанными в цифровой форме, выполняются проще.
Факториальная система счисления. Форма записи числа в факториальной системе имеет вид:
![]() .
.
Пример:
![]() ,
,
![]() .
.
Чтобы перейти от десятичной системы к факториальной, нужно начинать делить число не на основание, а на 2, затем І частное делить на 3, ІІ частное на 4 и т. д.
Пример:
|
_1236 |
2 |
|
|
|
|
|
|
1236 |
_618 |
3 |
|
|
|
|
|
0 |
618 |
_206 |
4 |
|
|
|
|
|
0 |
204 |
_51 |
5 |
|
|
|
|
|
2 |
50 |
_10 |
6 |
|
|
|
|
|
1 |
6 |
_1 |
7 |
|
|
|
|
|
4 |
0 |
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
![]() .
.
Таким образом, мы видим, что развитие вычислительной техники, появление быстродействующих программно-управляемых электронно-вычислительных машин, возникновение искусства программирования − всё это требует глубокого и целенаправленного изучения особенностей различных позиционных систем счисления и разработки новых альтернативных систем счисления, на основе которых могут быть построены вычислительные системы для ЭВМ.
Литература:
1. Гашков С. Б. Системы счисления и их применение / С. Б. Гашков:2-е изд., испр. и доп. — М.: изд-во МЦНМО, 2012. — 68 с.
2. Фомин С. В. Системы счисления / С. В. Фомин: 5-е изд., − М.: Наука, Гл. ред. Физ.-мат лит., 1987. — 48 с.

