Правила построения по законам геометрии были разработаны в эпоху античности. Поскольку одной из задач алгебры, начертательной геометрии является изучение методов построения различных пространственных форм, ее возможности значительно расширились с развитием вычислительной техники. Использование персональных компьютеров в инженерии привело к возникновению компьютерной графики, занимающейся созданием и обработкой изображений. Данная статья посвящена изучению вопросов инженерной графики, основанной на применении систем автоматизированного проектирования (САПР). Рассматриваются свойства и уравнения поверхностей вращения. Приводятся методики разработки 3D моделей поверхностей и реальных сооружений в САПР «Компас», а также натурных моделей с помощью 3D-печати.

Ключевые слова: математическое моделирование, САПР «Компас», поверхности вращения, 3D-печать

Цель исследования:исследование свойства поверхностей вращения через построение 3D моделей фигур и реальных сооружений с использованием системы автоматизированного проектирования (САПР) «Компас».

Задачи исследования:

1. Проанализировать специальную литературу, изучить различные виды поверхностей вращения, уравнения данных поверхностей и их свойства.
2. Рассмотреть области применения поверхностей вращения.
3. Изучить методы построения поверхностей вращения в САПР «Компас».
4. Построить 3D модели поверхностей и сооружений в САПР «Компас».

Поверхности вращения иих свойства

Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке O₁ — геометрическое место точек пространства, находящихся от точки O₁ на расстоянии R. При этом прямоугольная система координат (СК) в пространстве OXYZ позволяет установить взаимно однозначное соответствие между точками пространства и их координатами (x,y,z). Уравнением поверхности в прямоугольной СК OXYZ называется такое уравнение , которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности.

Поверхность вращения поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости. Пусть кривая L лежит в плоскости OYZ. Уравнения этой кривой можно представить в виде: (1)

Составим уравнение поверхности, образованной вращением кривой L вокруг OZ. Возьмем на поверхности точку M (x; y; z). Проведем через точку M плоскость, перпендикулярную OZ, обозначим точки пересечения с осью OZ и кривой L соответственно O₁ (0; 0; z) и N (0; y₁; z₁). Отрезки O₁M и O₁N — радиусы одной и той же окружности (O₁M = O₁N). Но , а . Значит, ,. Т. к. точка N лежит на кривой L, то ее координаты удовлетворяют системе (1). Исключив координаты y₁ и z₁ точки N, получим уравнение поверхности вращения: . Аналогично, если кривая вращается вокруг оси OY, то уравнение примет вид ; если кривая вокруг оси OX — .

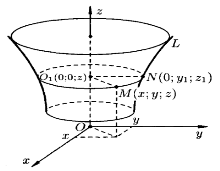
Рис. 1. Поверхность, образованная вращением кривой L вокруг оси OZ

Коническая поверхность (конус) — это поверхность, образованная прямыми линиями, проходящими через точку P и пересекающими плоскую линию L, не проходящую через точку P. Линия L называется направляющей конуса, точка P — вершиной, прямая, описывающая поверхность — образующей.

Пусть направляющая L задана системой: (2)

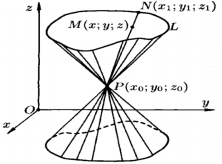
Рис. 2. Коническая поверхность

Точка — вершина конуса, точка принадлежит поверхности. Образующая, проходящая через P и M, пересекает L в точке . Координаты точки N удовлетворяют системе (2). Канонические уравнения образующих, проходящих через точки P и N, имеют вид: . (3)

Исключив переменные из уравнений (2) и (3), получим уравнение конической поверхности, связывающее координаты .

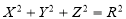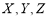
1. Эллипсоид. Рассмотрим сферу радиуса R с центром в начале координат: (4), где текущие координаты точки сферы. Сферой радиусаR называется множество точек пространства, расстояние от каждой из которых до центра равно R. Пусть сфера подвергнута равномерной деформации в направлении координатных осей Ox,Oy и Oz с коэффициентами деформаци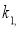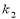и и 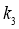.В результате сфера превратится в эллипсоид, а точка сферы M (X,Y,Z) перейдет в точку эллипсоида M′(x,y,z) причем: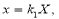 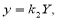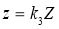. Отсюда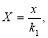 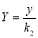, 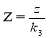. 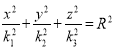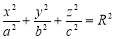Подставляя эти формулы в уравнение (4), получим: или , где .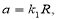

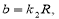
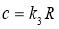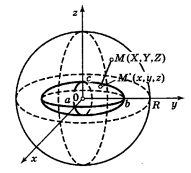
Рис. 3. Сфера и эллипсоид

Полученное уравнение связывает координаты точки M′ эллипсоида и является уравнением эллипсоида. Величины a,b,c называются полуосями; удвоенные величины 2a, 2b и 2c — осями и представляют его линейные размеры в направлениях деформации. Если a,b,c не равны между собой, то эллипсоид называется трехосным. Если две полуоси равны, он называется эллипсоидом вращения, т. к. может быть получен в результате вращения эллипса вокруг одной из его осей. Если a=b=c, то эллипсоид превращается в сферу.

Свойства эллипсоида:

1) Эллипсоид — ограниченная поверхность, поскольку из его канонического уравнения следует, что .

2) Эллипсоид обладает:

– центральной симметрией относительно начала координат;

– осевой симметрией относительно координатных осей;

– плоскостной симметрией относительно координатных плоскостей.

3) В сечении эллипсоида плоскостью, ортогональной любой из осей координат, получается эллипс.

2. Однополостный гиперболоид. Поверхность, задаваемая уравнением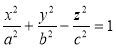, называется однополостным гиперболоидом. Название «гиперболоид» связано с тем, что среди сечений поверхности есть гиперболы. Например, сечения плоскостями x=0. Эти сечения представляются (в своих плоскостях) уравнениями:

, (x=0),(5)

(y=0).(6)

Поверхность представляет сплошную бесконечную трубку, вытянутую вдоль оси OZ. Плоскость z=hпри любом значении h дает в сечении с поверхностью эллипс с полуосями , (при этом a≠b):(z=h). (7)

Все эллипсы (7) подобны, вершины их лежат на гиперболах, задаваемых уравнениями (5) и (6); размеры эллипсов увеличиваются по мере удаления сечения от плоскости XOY. Сечение плоскостью XOY есть горловой эллипс:, который, вместе с гиперболами (5) и (6), называют главными сечениями.

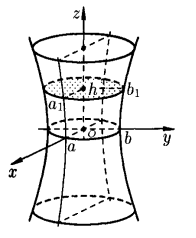
Рис. 4. Однополостный гиперболоид

Свойства однополостного гиперболоида:

1) Однополостный гиперболоид — неограниченная поверхность, поскольку из его канонического уравнения следует, что .

2) Однополостный гиперболоид обладает:

– центральной симметрией относительно начала координат;

– осевой симметрией относительно всех координатных осей;

– плоскостной симметрией относительно всех координатных плоскостей.

3) В сечении плоскостью, ортогональной оси координат , получается эллипс, а плоскостями, ортогональными осям или — гипербола.

4) Для каждой точки однополостного гиперболоида существует пара прямых, проходящих через эту точку и целиком лежащих на его поверхности.

3. Двуполостный гиперболоид. Поверхность, задаваемая уравнением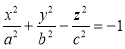, называется двуполостным гиперболоидом. Если поверхность пересечь плоскостями z=h, то линия пересечения определяется системой уравнений:

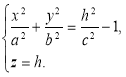. (8)

Отсюда следует, что:

– если |h|<с, то плоскости z=h не пересекают поверхности;

– если |h|=с, то плоскости z=±c касаются поверхности в точках (0;0:с) и (0;0;-с);

– если |h|>с, то система (7) может быть представлена следующим образом:

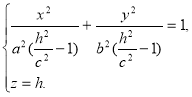
Данные уравнения задают эллипс, полуоси которого возрастают с ростом |h|. Пересекая поверхность плоскостями YOZ (x=0) и XOZ (y=0), получим в сечении гиперболы, уравнения которых соответственно имеют вид: , . Поверхность — две бесконечные чаши.

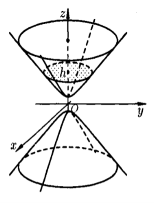
Рис. 5. Двуполостный гиперболоид

Свойства двуполостного гиперболоида.

1) Двуполостный гиперболоид — неограниченная поверхность, поскольку из его канонического уравнения следует, что и не ограничен сверху.

2) Двуполостный гиперболоид обладает:

– центральной симметрией относительно начала координат;

– осевой симметрией относительно всех координатных осей;

– симметрией относительно всех координатных плоскостей.

3) В сечении плоскостью, ортогональной оси координат , при получается эллипс, а плоскостями, ортогональными осям или — гипербола.

4. Эллиптический параболоид. Поверхность, задаваемая уравнением 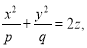где p>0, q>0 называется эллиптическим параболоидом. Рассечем поверхность плоскостями z=h. В сечении получим линию, уравнение которой 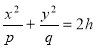. Если h<0, то плоскости z=h поверхности не пересекают; если h=0, то плоскость z=0 касается поверхности в точке (0; 0; 0); если h>0, то в сечение — эллипс, уравнение которого 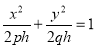, z=h. При пересечении поверхности плоскостями XOZ и XOY получается параболы 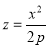и . 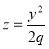Поверхность имеет вид выпуклой, бесконечно расширяющейся чаши.

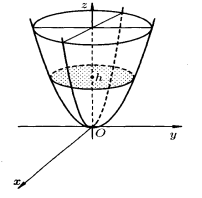
Рис. 6. Эллиптический параболоид

Свойства эллиптического параболоида.

1) Эллиптический параболоид — неограниченная поверхность, т. к. из его уравнения следует, что и принимает сколь угодно большие значения.

2) Эллиптический параболоид обладает

– осевой симметрией относительно оси ;

– плоскостной симметрией относительно плоскостей и .

3) В сечении эллиптического параболоида плоскостью, ортогональной оси , получается эллипс, а плоскостями, ортогональными осям или — парабола.

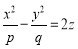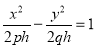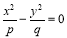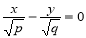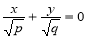5. Гиперболический параболоид. Поверхность, задаваемая уравнением , где p>0, q>0 называется гиперболическим параболоидом. Рассечем поверхность плоскостями z=h. Получим кривую , z=h, которая при всех значениях h≠0 является гиперболой. При h>0 оси параллельны оси OX; при h<0 ― параллельны оси OY; при h=0 линия пересечения распадается на пару пересекающихся прямых и . При пересечении поверхности плоскостями, параллельными XOZ, получим параболы 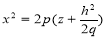, ветви которых направлены вверх. При y=0 в сечении получается парабола 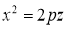с вершиной в начале координат и осью OZ. Пересекая поверхность плоскостями x=h, получим параболы 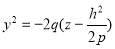, ветви которых направлены вниз. Поверхность имеет вид седла.

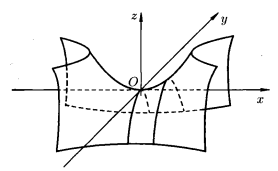
Рис. 7. Гиперболический параболоид

Свойства гиперболического параболоида.

1) Гиперболический параболоид — неограниченная поверхность, поскольку из его канонического уравнения следует, что — любое.

2) Гиперболический параболоид обладает

– осевой симметрией относительно оси ;

– плоскостной симметрией относительно плоскостей и

3) В сечении плоскостью, ортогональной , получается гипербола, а плоскостями ортогональными или — парабола. Т.о. поверхность может быть получена перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости перпендикулярны.

4) Для каждой точки гиперболического параболоида, существует пара прямых, проходящих через эту точку и целиком лежащих на поверхности.

6. Конус второго порядка. Исследуем поверхность, задаваемую уравнением 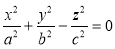Пересечем поверхность плоскостями z=h. Линия пересечения будет определяться уравнением 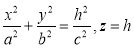. При h=0 она вырождается в точку (0;0;0). При h≠0 в сечении будем получать эллипсы 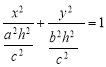, z=h. Рассечем поверхность плоскостью YOZ. Получится линия 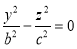, распадающаяся на две пресекающиеся прямые 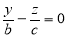и 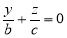. При пересечении поверхности плоскостью y=0 получим линию 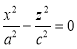, также распадающуюся на две пересекающиеся прямые 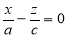и .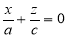

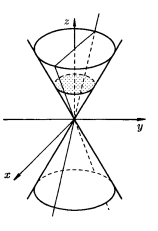
Рис. 8. Конус второго порядка

Таким образом, поверхность имеет вид, изображенный на рисунке 8. Подобные поверхности, составленные из прямых линий, называются линейчатыми. Такими поверхностями являются цилиндрические, конические поверхности, а также однополостный гиперболоид и гиперболический параболоид.

Моделирование поверхностей второго порядка вСАПР «Компас»

КОМПАС-3D ― система автоматизированного проектирования (САПР), разработанная российской компанией «АСКОН». Она позволяет автоматизировать проектно-конструкторские работы, создавать трехмерные параметрические модели, подготавливать документацию. Система имеет простой интерфейс, эффективный и удобный набор управляющих команд, большой список библиотек, а также обладает возможностью компьютерного проектирования в соответствии с правилами оформления конструкторской и строительной документации, принятыми в России.

В системе КОМПАС-3D трехмерную модель можно построить с использованием двух технологий: моделирование твердых тел и поверхностное моделирование. Их совместное использование позволяет решать самые разнообразные конструкторские задачи. Построение трехмерной твердотельной модели заключается в последовательном выполнении операций объединения, вычитания и пересечения над объемными элементами, из которых и состоит большинство механических деталей.

Построение моделей поверхностей второго порядка в САПР «Компас» может осуществляться несколькими методами. Наиболее простой заключается в создании фигуры и вращения ее вокруг оси. Рассмотрим процесс построения эллипсоида.

Эллипсоид.Для начала необходимо создать эллипс. Затем провести центральную осевую линию двумя способами: вертикально и горизонтально. Следующим действием будет усечение половины эллипса вертикально и горизонтально. И наконец, с помощью функции вращения создаем эллипсоид с вертикальной или горизонтальной осью вращения.

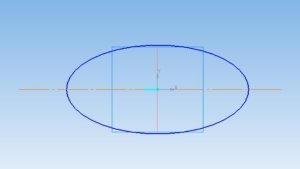
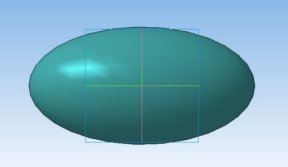
Рис. 9. Эллипсоид с вертикальной и горизонтальной осью вращения

Если поверхность задается путем вращения некоторой кривой, то для ее построения в САПР «Компас» используется кинематический метод задания поверхности. Таким способом можно построить, например, параболоид или гиперболоид. Метод основывается на том факте, что парабола и гипербола являются кониками — т. е. кривыми, получаемыми при рассечении конуса плоскостью. Процесс создание моделей состоит из этапов:

1. Построить ось вращения и образующую конуса.
2. Применить операцию вращения. В результате получится конус.
3. Рассечь конус плоскостью по параболе или гиперболе.
4. Скопировать кривую, начертить ось и выполнить вращение.

Алгоритм построения 3D модели эллиптического параболоида:

1. Создаем новый документ типа «Деталь».
2. Выбираем рабочую плоскость, чертим ось вращения и образующую конуса (прямую, пересекающую ось). Применяем операцию «Вращение».
3. Вводим две вспомогательные плоскости: первая — касательная к поверхности конуса, вторая — параллельная первой (операция — «Плоскость/Смещенная»).
4. Пересекаем вторую плоскость с поверхностью конуса с помощью операции «Кривая пересечения». В качестве параметров указываем коническую поверхность и вспомогательную плоскость. Получаем искомую параболу.
5. Вводим третью вспомогательную плоскость и проецируем на нее параболу.
6. Включаем режим эскиза, вычерчиваем ось параболы, удаляем одну ветвь.
7. Вызываем операцию «Вращение» и получаем искомый параболоид.

Скриншоты некоторых этапов построения модели параболоида в САПР «Компас», а также фотографии этапов 3D печати приведены ниже.

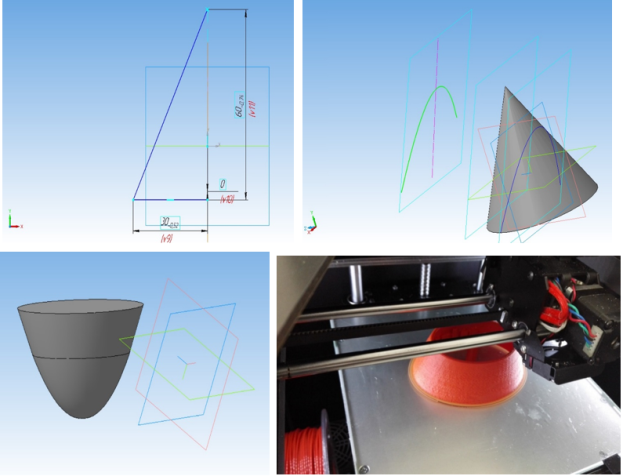
Рис. 10. 3D-модель эллиптического параболоида

Поверхности вращения имеют весьма широкое применение во многих областях техники и архитектуры. Например, форму параболоида имеют спутниковая антенна, рефлектор (отражатель), высокочувствительный направленный микрофон и т. д. Некоторые здания также создаются в форме поверхностей вращения. Примером усеченного эллипсоида служит небоскреб Swiss Re в центре Лондона. Здание имеет 40 этажей. Конструкция небоскреба выполнена в виде сетчатой оболочки с центральным опорным основанием. Он не имеет углов, что не позволяет ветровым потокам стекать вниз. Диаметр здания у основания составляет 49 метров, затем здание плавно расширяется, достигая максимального диаметра в 57 метров на уровне 17 этажа. Далее конструкция сужается, достигая минимального диаметра в 25 метров. Здание практически полностью стеклянное, его верхушка закрыта прозрачным куполом. Название небоскреба ― Башня Мэри-Экс.

Модель здания можно разработать с использованием САПР «Компас». Однако из-за очевидной архитектурной сложности процесс создания модели более сложный и включает много этапов. Ниже приведены фотографии 3D печати модели.

Рис. 11. 3D-модель башни Мэри-Экс

Другимпримером может служить Шуховская башня (Шаболовская телевизионная башня) — гиперболоидная конструкция, выполненная в виде несущей стальной сетчатой оболочки. Расположена в Москве на улице Шухова. Построена в 1920–1922 годах по проекту академика В. Г. Шухова. Башня имеет сетчатую конструкцию, благодаря чему достигается минимальная ветровая нагрузка, представляющая главную опасность для высоких сооружений. По форме секции башни — это однополостные гиперболоиды вращения, сделанные из прямых балок, упирающихся в кольцевые основания. Ажурная конструкция сочетает в себе прочность и легкость: на единицу высоты Радиобашни Шухова израсходовано в три раза меньше металла, чем на единицу высоты Эйфелевой башни в Париже. Круглый конусный корпус башни состоит из 6 секций высотой 25 метров. Нижняя секция установлена на бетонном фундаменте диаметром 40 метров и глубиной 3 метра.

Алгоритм построения и печать 3D модели фрагмента Шуховской башни.

1. Создаем новый документ типа «Деталь».
2. Выбираем рабочую плоскость, чертим три окружности диаметрами 100, 80 и 60 с центром в начале координат.
3. Чертим две касательные ко второй окружности, проходящие через общую точку, расположенную на первой окружности (инструменты «Отрезок» и «Касание»).
4. Выравниваем полученные точки относительно вертикальной оси (оси OY) с помощью соответствующего инструмента.
5. Строим дугу между полученными двумя точками на второй окружности.
6. Применяем операцию «Вращение» к полученной фигуре.
7. Выбираем одну из граней фигуры и переходим в режим «Эскиз».
8. С помощью инструментов «Непрерывный ввод объектов», «Параллельность» и «Перпендикулярность» строим прямоугольник, одна из сторон которого является диагональю грани фигуры.
9. Задаем ширину прямоугольника = 2.
10. Повторяем этапы 8 и 9 для второй грани фигуры.
11. С помощью операции «Вращение» (свойство «Результат операции» — «Новое тело»), примененной для прямоугольников, получим две пересекающиеся трубки.
12. Скроем исходную фигуру.
13. Создадим «Массив по концентрической сетке» из полученных стержней. Количество элементов массива = 10.
14. В результате получим искомую модель.

Скриншоты некоторых этапов построения модели в САПР «Компас», а также фотографии этапов 3D печати приведены ниже.

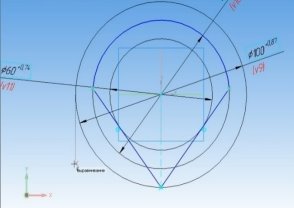
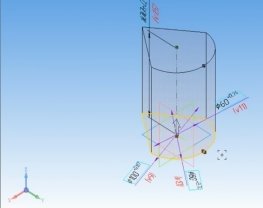
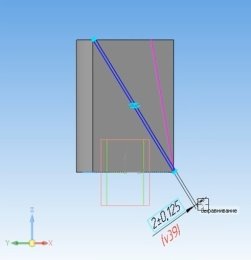
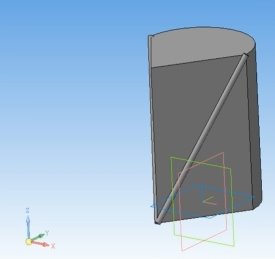
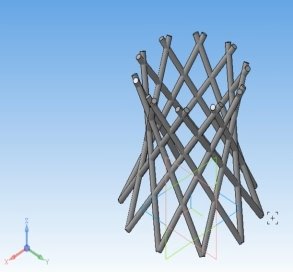
Рис. 12. 3D-модель Шуховской башни

Заключение

В ходе проведенного исследования были изучены методы задания уравнений поверхности вращения и некоторые их свойства. Также были рассмотрены методы построения 3D моделей данных поверхностей с помощью САПР «Компас», описаны методики построения некоторых моделей. Кроме того, изучены возможности данной системы для решения поставленных задач. По результатам проведенной работы были созданы реальные 3D модели поверхностей с помощью технологии 3D печати.

Таким образом, можно сделать вывод, что изучение способов построенияповерхностей вращения, их свойств, а также методов построения 3D моделей с помощью САПР «Компас», позволяет рассмотреть некоторые вопросы математики, информатики с разных позиций, проследить взаимосвязь данных предметов, повысится уровень знаний в области применения средств ИКТ к решению математических задач. Все это непременно может помочь в дальнейшем получении профессии.

Литература:

1. Выгодский М. Я. Справочник по высшей математике. ― М.: Астрель АСТ, 2006.
2. Золотарёва Д. А., Кравцова К. Е. Разработка методических рекомендаций по моделированию параболоида и гиперболоида средствами программы Компас-3D. — Инженерная графика и трехмерное моделирование. Молодежная научно-практическая конференция: сборник научных докладов (16 декабря 2016г., Новосибирск). — Новосибирск: СГУГиТ, 2017.
3. Кидрук М. КОМПАС-3D V10 на 100 %. — СПб.: Питер, 2009.
4. Письменный Д. Т. Конспект лекций по высшей математике. ― М.: Айрис-Пресс, 2009.
5. Талалай П. Г. Компьютерный курс начертательной геометрии на базе КОМПАС-3D. — СПб.: БХВ-Петербург, 2010.
6. Информационный портал Cubicprints [Электронный ресурс]. URL: http://www.cubicprints.ru/tutorials/kak-redaktirovat-3d-model-v-netfabb-Basic (Дата обращения: 10.02.2017г.)