Разработка математических моделей процессов очистки и джинирования
Авторы: Юсупов Фирнафас, Алиев Ойбек Азадович
Рубрика: Спецвыпуск
Опубликовано в Техника. Технологии. Инженерия №2 (4) апрель 2017 г.
Дата публикации: 04.05.2017
Статья просмотрена: 340 раз
Библиографическое описание:
Юсупов, Фирнафас. Разработка математических моделей процессов очистки и джинирования / Фирнафас Юсупов, О. А. Алиев. — Текст : непосредственный // Техника. Технологии. Инженерия. — 2017. — № 2.1 (4.1). — С. 56-57. — URL: https://moluch.ru/th/8/archive/57/2342/ (дата обращения: 19.04.2024).
Для построения многомерных статистических математических моделей технологических процессов очистки и джинирования (отделение волокна от семени) хлопка-сырца использован метод Брандона.
Ключевые слова: технологический процесс, математическое моделирование, эксперимент, метод Брандона, первичная обработка хлопка
For the construction of multidimensional statistical mathematical models of technological processes of purification and Separation of fiber from seed
(Ginning) of raw cotton, the Brandon method was used.
Keywords. Technological process, mathematical modeling, experiment, Brandon's method, primary cotton processing
Одним из сложных методических вопросов автоматизированного управления ходом производственного процесса хлопкоперерабатывающихся предприятий является создание комплексных математических моделей различного функционального назначения, отличающихся программно-алгоритмическими и техническими особенностями, временем реакции и периодичностью выполнения функции.
Для разработки алгоритмов планированная и управления процессом первичной обработки хлопка-сырца необходимо иметь математическую модель объекта управления (регулирования), являющуюся формализованным описанием структуры производства и характеризующую его параметры.
Математическая формализация исследуемого процесса сводится к построению статической модели оперативного регулирования хода технологического процесса первичной обработки хлопка-сырца, а также к определению закона совместного распределения интенсивностей выпуска конечных (промежуточных) продуктов требуемого качества при фиксированных параметрах технологического процесса и интенсивностях использования дискретных технологических режимов.
Исследуемый непрерывный технологический процесс первичной обработки хлопка-сырца является многоступенчатым процессом с последовательной структурой [1,2]. Известно, что сложность математической модели производственного процесса определяется количеством структурных элементов и конфигурацией связей между ними.
Для построения модели многомерного технологического объекта в настоящее время существуют несколько методов. Можно использовать метод множественной корреляции, метод группового учета аргументов, метод главных компонент, метод Брандона [3,4] и др. Однозначно отдать предпочтение одному из методов нельзя, поскольку каждый из них связан с особенностями конкретного технологического объекта.
В работе для построения статистической модели использован метод Брандона.
Для построения статистических математических моделей технологических процессов очистки и джинирования хлопка-сырца был использован данный метод. Сущность этого метода математического моделирования заключается в следующем:
Уравнение регрессии идентифицируемого объекта представляется в виде
![]() (1)
(1)
Здесь ![]() произвольная функция величины
произвольная функция величины ![]() . Порядок расположения переменных
. Порядок расположения переменных ![]() в выражении (1) оказывает существенное влияние на точность обработки результатов экспериментальных данных, а именно чем большее влияние на функциональный признак оказывает переменная
в выражении (1) оказывает существенное влияние на точность обработки результатов экспериментальных данных, а именно чем большее влияние на функциональный признак оказывает переменная ![]() тем меньше должен быть порядковый номер индекса j. Вид и форма функций
тем меньше должен быть порядковый номер индекса j. Вид и форма функций ![]() выбирается на основе построения эмпирических линий регрессии. В начале по точкам выборки системы величин
выбирается на основе построения эмпирических линий регрессии. В начале по точкам выборки системы величин ![]() строятся поле корреляции и эмпирическая линия регрессии
строятся поле корреляции и эмпирическая линия регрессии ![]() . На основе этого определяется тип зависимости
. На основе этого определяется тип зависимости ![]() и методом наименьших квадратов вычисляются коэффициенты этого уравнения регрессии. После составляется выборка новой величины:
и методом наименьших квадратов вычисляются коэффициенты этого уравнения регрессии. После составляется выборка новой величины:
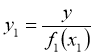 (2)
(2)
Рассчитанная величина ![]() уже не зависит от
уже не зависит от ![]() , а определяется только параметрами
, а определяется только параметрами ![]() . В соответствии с этим можно написать:
. В соответствии с этим можно написать:
![]() (3)
(3)
Но точкам новой выборки величин![]() и
и ![]() вновь строятся корреляционное поле и эмпирическая линия регрессии, характеризующая зависимость
вновь строятся корреляционное поле и эмпирическая линия регрессии, характеризующая зависимость ![]() от
от ![]() :
:
![]()
Вычисляются её коэффициенты и вновь составляется выборка новой величины:
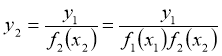 (4)
(4)
Рассчитанная величина ![]() уже не зависит от двух факторов
уже не зависит от двух факторов ![]() и
и ![]() и может быть определена не следующего уравнения регрессии:
и может быть определена не следующего уравнения регрессии:
![]() (5)
(5)
Указанная процедура определения функций ![]() продолжается до получения выборки величины
продолжается до получения выборки величины ![]() :
:
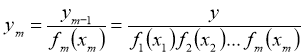 (6)
(6)
Рассчитанная величина ![]() не зависит от всех переменных
не зависит от всех переменных ![]() определяется коэффициентом исходного уравнения
определяется коэффициентом исходного уравнения
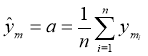 (7)
(7)
здесь n — объем выборки.
Для реализации метода Брандона была составлена программа MAIN на алгоритмическом языке С++ для персональныхЭВМ.
В результате обработки экспериментальных данных, по алгоритму метода Брандона получены следующие регрессионные уравнения:
1) для засоренности по крупному сору –
![]() (8)
(8)
2) для засоренности по мелкому сору –
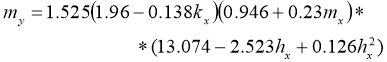 (9)
(9)
3) для влажности хлопка-сырца
![]() (10)
(10)
Для технологического процесса джинирования получены уравнения регрессии:
4) для влажности волокна –
![]() (11)
(11)
5) для содержания пороков и сора в волокне -
![]()
6) для влажности семян –
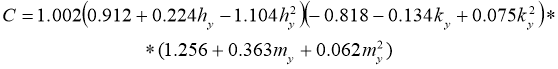
7) для засоренности семян
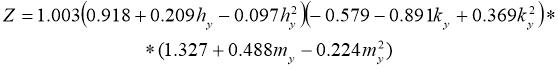
Опыт использования математических моделей для прогнозирования и управления показал их достаточную точность. Однако при решении задач управления эти модели оказались несколько громоздки. В связи е этим представилось возможным без существенной потери точности упростить некоторые полученные уравнения. Полученные упрошенные математические модели в дальнейшем будет использованы для выбора плана первичной обработки хлопка-сырца.
Литература:
- Регламентированный технологический процесс первичной обработки хлопка-сырца. — М.: Легкая индустрия, 1982. — 116 с.
- Джаббаров Г. Д., Отаметов Т. У., Хамидов А. Первичная обработка хлопка. — Т.: Укитувчи,1987. — 328 с.
- Ахназарова С. Л., Кафаров В. В. Методы оптимизации эксперимента в химической технологии. М.: Высш. шк., 1985. — 326 с.
- Пантелеев А. В., Летова Т. А. Методы оптимизации в примерах и задачах (учебное пособие). М.: Высшая школа, 2002. — 544 с.
Ключевые слова
математическое моделирование, эксперимент, технологический процесс, метод Брандона, первичная обработка хлопкаПохожие статьи
Автоматизация проектирования процесса математического...
Многоступенчатый производственный процесс первичной переработки хлопка-сырца для целей объемного (текущего) планирования предлагается методом агрегирования свести к двум обобщенным операциям – «джинирования» и «линтерования» [1]. Предлагается управление...
Методы моделирования случайных процессов
Для построения моделей технологических процессов первичной обработки хлопка-сырца.
О моделировании дискретно-непрерывных процессов. Теория вероятностей, случайные процессы, математическая статистика и приложения.
Технологический процесс массового изготовления швейных...
Процесс первичной обработки хлопка (ПОХ) хлопкоперерабатываемой промышленности относится к технологическим процессам производства
1. низкая точность оперативной информации, о движении хлопка-сырца по всем стадиям производственного процесса — от...
Разработка линейных математических моделей...
Разрабатывается упрошенные математические модели технологического процесса дробления семян хлопчатника с целью их использования для оперативного управления ходом производства.
Уравнения регрессии приняло вид.
Рекомендации по составлению статических моделей...
Для построения моделей технологических процессов первичной обработки хлопка-сырца можно выделить два подхода: 1) физико-механический анализ явлений» обуславливающих динамику процесса
Экономико-математическое моделирование производственных...
Взаимные процессы между биологическими, технологическими
Моделирование – процесс построения модели, которая изучает поведение объектов разной природы.
Математическая модель – система математических формул, неравенств или уравнений, которая с большей...
Проблема применения математического моделирования...
Моделирование производственных процессов предприятий...
процесс, промышленное предприятие, технологический процесс, ISO, общий менеджмент, математическая статистика, корреляционный анализ, жизненный цикл, готовый продукт, MSPC.
Построение фреймовой модели технологических задач сушки...
Первичная обработка хлопка-сырца требует снижения влажности до 8 %, так как в противном случае качество волокна ухудшается, что частично объясняется повышенной сцепляемостью волокна с сорными примесями, затрудняющей их удаление в процессе очистки.
Математическая модель технологического процесса...
Математическая модель технологического процесса обогащения каолина. Автор: Камолов Эшмурод Рахмонович.
При этом процесс использования субстрата бактериями можно представить в виде следующего уравнения: (3).
Похожие статьи
Автоматизация проектирования процесса математического...
Многоступенчатый производственный процесс первичной переработки хлопка-сырца для целей объемного (текущего) планирования предлагается методом агрегирования свести к двум обобщенным операциям – «джинирования» и «линтерования» [1]. Предлагается управление...
Методы моделирования случайных процессов
Для построения моделей технологических процессов первичной обработки хлопка-сырца.
О моделировании дискретно-непрерывных процессов. Теория вероятностей, случайные процессы, математическая статистика и приложения.
Технологический процесс массового изготовления швейных...
Процесс первичной обработки хлопка (ПОХ) хлопкоперерабатываемой промышленности относится к технологическим процессам производства
1. низкая точность оперативной информации, о движении хлопка-сырца по всем стадиям производственного процесса — от...
Разработка линейных математических моделей...
Разрабатывается упрошенные математические модели технологического процесса дробления семян хлопчатника с целью их использования для оперативного управления ходом производства.
Уравнения регрессии приняло вид.
Рекомендации по составлению статических моделей...
Для построения моделей технологических процессов первичной обработки хлопка-сырца можно выделить два подхода: 1) физико-механический анализ явлений» обуславливающих динамику процесса
Экономико-математическое моделирование производственных...
Взаимные процессы между биологическими, технологическими
Моделирование – процесс построения модели, которая изучает поведение объектов разной природы.
Математическая модель – система математических формул, неравенств или уравнений, которая с большей...
Проблема применения математического моделирования...
Моделирование производственных процессов предприятий...
процесс, промышленное предприятие, технологический процесс, ISO, общий менеджмент, математическая статистика, корреляционный анализ, жизненный цикл, готовый продукт, MSPC.
Построение фреймовой модели технологических задач сушки...
Первичная обработка хлопка-сырца требует снижения влажности до 8 %, так как в противном случае качество волокна ухудшается, что частично объясняется повышенной сцепляемостью волокна с сорными примесями, затрудняющей их удаление в процессе очистки.
Математическая модель технологического процесса...
Математическая модель технологического процесса обогащения каолина. Автор: Камолов Эшмурод Рахмонович.
При этом процесс использования субстрата бактериями можно представить в виде следующего уравнения: (3).







