Algorithm of Calculation of Factors in Piecewise-Quadratic Harmut’s Bases



В работе приведены примеры аналитические установленные и показаны экспериментально полученных зависимостей преимуществ разработанного алгоритма спектрального преобразования в базисе кусочно-квадратичной функции Хармута. Предлагаемая система и алгоритм могут найти широкое применение в таких областях, как компьютерной графики, обработки изображений и восстановления, машинного зрения и мультимедиа, анимации и производства компьютерных игр.

Abstract. In work the examples of analytically set and experimentally received dependences advantages of the developed algorithm of spectral transformation in basis of piecewise-quadratic Harmut’s functions are shown. The offered system and algorithm on its basis can find wide applications in such areas, as computer graphic, images processing and restoration, machine vision and multimedia, animation and manufactures of computer games.

Keywords: graph, basic functions, fast transformations.

One of the basic features of orthogonal bases is presence of fast algorithms for definition of spectral factors. Fast algorithms allow to reduce quantity of arithmetic operations and volume of necessary memory. The increase in speed is as a result reached at use of orthogonal bases for digital processing signals [1, 2, 3, 4].

We write down the formula of direct and return fast spectral transformations for sequence of readout of a signal { xi } for any valid orthogonal piecewise-constant basis

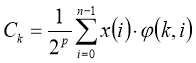(1)

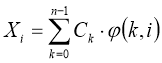, (2)

where k = number of spectral coefficient,

i = number of an element of sequence of the valid readout.

In this graph, the continuous lines correspond to operations of addition, while the hatch lines are operations of subtraction. Entrance readout is denoted with Х₀, Х₁,..., Х₁₅, and results are denoted with С₀, С₁, С₂..., С₁₅

The analysis of computational methods of factors in various bases has shown, that fast algorithms for calculation of factors exist only for piecewise-constant and piecewise-linear bases. Algorithms of calculation of factors in piecewise-quadratic bases have not been developed.

We investigate a question how algorithms of fast transformations in bases of orthogonal piecewise-constant functions can be adapted for calculation of factors in piecewise-linear bases. Known formulas Fourier — Haar [1, 5], Fourier — Harmut using integrals of a kind:

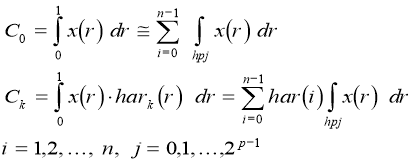(3)

applicable only in the event that transformable signals x (r) belong to metric space L2 [0,1).

The algorithm of calculation of factors does not possess property of fast transformation and, besides if necessary to receive values of factors in локализуемых bases it is possible to use directly operations with final differences.

For example, factors in basis Shauder are calculated on the basis of transformations

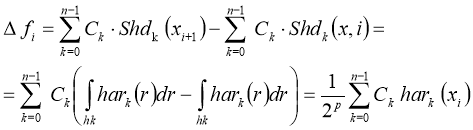(4)

The analysis of Harmut’s matrix

helps to develop new algorithm of fast transformation. Factors С₀ and С₁ are decomposed with Harmut’s basic functions. The zero and first order are defined respectively by the following formulas:

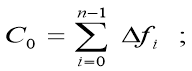
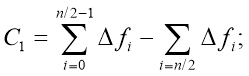
For the second order of basic functions factors of Harmut’s fast transformation С₂ and С₃ are calculated by grouping the sums of final differences under formulas:

;

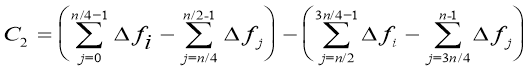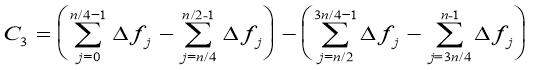
Other factors for P ≥ 2, k ≥ 4 are calculated as the sum of a difference of a following view:

Results

Series of numerical experiments have been carried out on the research of piecewise-quadratic bases. With use of the offered algorithm of calculation of coefficients in Haar and Harmut’s piecewise-quadratic bases, “Table-1” is achieved. Here the factor of compression Кс is defined by the formula:

К_с=N/(N-N₁),

Where N — Quantity of readout of function N1 — Quantity of the zero factors received as a result of use of offered algorithm.

The numerical experiments allow us to draw a conclusion that the number of zero coefficients at digital processing of signals received as a result of bench tests in Haar and Harmut’s piecewise-quadratic bases ranges from 5 % up to 17 %, when processing the geophysical signals received as a result magnetic exploration we get values ranging from 5 % up to 25 %, and while processing elementary functions (and also functions consisting of their combinations) this parameter gives us value from 10 % up to 70 % with an accuracy of 10–4-10–6. It is established, that decomposition (4) allows receiving high speed in Haar’s basis and the big factor of compression in Harmut’s basis. Also as a result of researches it is revealed, that with increase in quantity of readout function N, the values of factors decreases on exponential law.

Conclusion. As a result of research on methods of approximating functional dependence shows their limitation as weak convergence, discontinuity, rather low accuracy of approximation, necessity of great volume of memory for factors are revealed. In order to overcome these limitations, the necessity for transition to piecewise-quadratic bases was shown. Advantages of piecewise-quadratic bases: greater accuracy and good smoothness of approximation in comparison with piecewise-constant and piecewise-linear bases. The method is based on applications of good differential properties of basic splines, it is hardware-focused and allows to use existing algorithms of fast transformations in bases of orthogonal piecewise-constant functions for calculation of factors both piecewise-linear and piecewise-quadratic bases.

Reference

1. Harmut H. Information transfer by orthogonal functions. –M.: Mir, 1975. -272 p.
2. F. Schipp, W. R. Wade, P. Simon and J. P´al, Walsh Series. An Introduction to Dyadic Harmonic Analysis, Adam Hilger, Bristol, 1990.
3. M. Sobol’, Multidimensional Quadrature Formulas and Haar Functions, Nauka, Moscow, 1969 (in Russian).
4. M. Sobol’ and O. V. Nuzhdi n, A new measure of irregularity of distribution, J. Number Theory 39 (1991), 367–373.
5. Hsein-Ping Kew, Hakimjon Zayniddinov, Dannanjay Singh, Do-Un Jeong. Specialized Processor and Algorithm for Signal Processing in Piecewise-polynomial Bases. The 5th International Conference on Intelligent Manufacturing & Logistics Systems (IML 2009), Kitakyushu, Japan, February 16 -18, 2009, p 47–51.