В этой статье написано об алгоритмах удаления невидимых линий и плоскостей. Алгоритм Робертса. Алгоритм Z буфер метода.
Ключевые слова: Алгоритм Робертса, Z буфер, проекция, невидимые линии, невидимые плоскости, грань, многогранник.
Annotation: This article is written about the algorithms remove hidden lines and planes. Roberts algorithm. Z buffer algorithm method.
Keywords: Roberts algorithm, Z buffer, projection, hidden lines, invisible plane face polyhedron.
Бирор бир уч ўлчовли объектни икки ўлчовли текисликда (компютер экранида) қуриш учун аввало уни қайси қисмлари кўринарли, қайси қисмлари кўринмас, яни объектнинг бошқа ёқлари билан ёпиқлигини аниқлаш керак. Проекциялашда марказий ёки паралел проекциялаш ишлатилади [4,31].
Проекциялашда проекторлар объектнинг ҳар бир нуқтасидан ўтади. Проекциялаш йўналиши буйича тасвир текислигига яқинрок масофадаги нуқталар кўринадиган ҳисобланади. Содда кўринганлигига қарамай ушбу масалани ечиш анча қийинчиликларга ва айрим ҳолларда бироз ҳисоб китобларга олиб келади. Ушбу масалани ечишда компютер графикасида иккита асосий ёндашиш мавжуд:
1. Проекциялаш йўналиши бўйича тасвир текислигига якинроқ масофада жойлашган объектнинг нуқталарини аниқлаш. Бунда дисплейнинг растр хоссаларидан фойдаланилади.
2. Объектларни ёки объект қисмларини ўзаро таққослаб объектларни ёки объект қисмларини кўринишлигини аниқлаш. Икки ёндашишни ўзаро ичига олувчи алгоритмлар ҳам мавжуд. [1,58].
Кўринмас ёқларни ажратиш. Ҳар ёқлари учун ташқи бирлик нормал вектори n берилган кўп ёқликни кўрамиз.
Агар ёқнинг нармал вектори n ва проекциялаш йўналишини берувчи вектор l ўртасидаги бурчак ўтмас бўлса у ҳолда қаралаётган ёқ кўринмайди ва кўринмас ёқ деб аталади. Агар мос бўлган бурчак ўткир бўлса у ҳолда қаралаётган ёқ кўринадиган ёқ дейилади. Параллел проекциялашда бурчакка қуйиладиган шартни қуйидагича ёзиш мумкин:
(n,l)=(n1l1+n2l2+n3l3)≤ 0
Ушбу шарт бажарилса ёқ кўринмас.
Ёқнинг ихтиёрий R нуқтасини маркази S нуқтада жойлашган марказий проекциялашнинг йўналиш вектори қуйдагича топилади:
L=S-R
Ва сўнг ёқнинг ихтиёрий R нуқтаси учун шарт текширилади
(n,l)≤ 0.
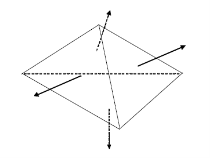
Кўринмас чизиқларни (қирраларни) чиқариб юбориш (четлатиш) Роберт алгоритими. Қавариқ кўпбурчаклардан тузилган объектнинг кўринмас қирраларинини чиқариб юбориш алгоритми Роберт алгаритми бўлади. Ушбу алгоритмни келтирамиз. [2,79].
Дастлаб иккита аниқловчи ёқларни кўринмайдиган бўлган қирралар чиқариб юборилади. Кейинги қадамларда қолган қирралар ҳар бир ёқлар билан ёпиқликка текширилади. Учта ҳолат мавжуд ва текширилади:
1. Ёқ қиррани ёпмайди, бу ҳолда қирра чиқариб ташланмайди.
2. Ёқ қиррани тўлик ёпади, бу ҳолда қирра чиқариб юборилади.
3. Ёқ қиррани қисман ёпади, бу ҳолда қирра бир неча бўлакларга бўлинади. Қирра кўрилган кирралар рўйхатига қирранинг ёк билан ёпилмайдиган кисимлари кўйилади.
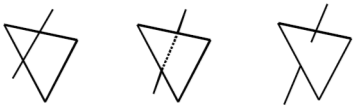
Кўринмас ёқларни чиқариб юбориш. З буфер усули. Кўринмас чизиқ ва сиртларни чиқариб юбориш алгоритимларидан бири бу Z буфер усули бўлади.
Бу усул биринчи ёндошишга тўғри келади ва ҳар бир нуқта билан ишлайди. Тасвир текислигидаги ҳар бир нуқтага (пикселга) (x,u) рангдан ташқари у хотирада сақланади. Дастлаб уни (чуқурлик)+∞ тенг деб ҳисоблаймиз. Ихтиёрий ёқни тасвир текислигига тасвирлаш учун унинг ҳар бир пиксели учун Z чуқурлиги ҳисобланади. Агар у дастлабки чуқурлигидан кичик бўлса бу қиймат Z буфери киритилади ва ески қиймати чиқарилиб юборилади. Ва Z буферидаги пикселлар экранда чиқарилади. Кўшни пикселларни Z чуқурлигини ҳисоблашни бутун қиймати Брезенхейм алгоритимидан фойдаланиш тавсия етилади. Айтиш жоизки Z координация қиймати объектларнинг ёруғлигини беришда ёки уларни умуман чиқариб юборишда кенг қўлланилади.
Тартиблаш алгоритимлари. Чуқурлиги бўйича тартиблаш усули. Ёқларни тартиблашнинг енг оддий алгоритими бу уларнинг проекциялаш йўналиши бўйича тасвир текислигигача бўлган минимал масофа бўйича тартиблаш ҳисобланади. Уларни яқинлашиш тартибида чиқариш мақсадида OZ ўқи бўйича паралел проекциялашни кўрамиз. Фараз қиламизки, бизга R ва Q yoqlari berilgan bo’lsin. Уларни тасвир текислигида (компютер экранида) тартибланган ҳолда чиқариш учун 5 та шартни текшириш тавсия этилади. Уларни текшириш мураккаблиги ошиши тартибида келтирамиз:
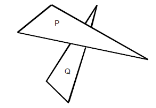
1. OX ўқидаги ёқларни проекциялари кесишадими?
2. OY ўқидаги уларнинг проекциялари кесишадими?
3. R ёки Q ёқидан ўтувчи текислигига нисбатан координаталар боши ётадиган томонида ётмайди.
4. Q ёки P ёкидан ўтувчи текислигига нисбатан координаталар боши ётадиган томонидан ётади.
5. Ёқларнинг тасвир текислигидаги проекциялари ўзаро кесишади. Агар келтирилган шартлардан бирортаси инкор бўлса R ёки Q ёқига нисбатан тасвир текисликка яқинрок жойлашади ва куйдагича тасвирланади:
Фойдаланилган адабиётлар:
- Назиров Ш.А., Нуралиев Ф.M., Тўраев Б.З. Компьютер графикаси ва дизайн. Т.: 2015.-256 б.
- Мамаражабов M.E., Турсунов С.Қ., Набиулина Л.M. Компьютер графикаси ва web - дизайн. T.: 2013.
- Назиров Ш.A., Нуралиев Ф.М, Тиллаева M.A. Растр графикаси, Тошкент,2012.
- Шикин Е.В., Борссков А.В. Компьютерная графика. Динамика, реалистические изображения. М. 1996. 288 с.

