Моделирование детектора следовых количеств опасных веществ



Актуальность проблемы, связанной с террористическими актами, не нуждается в объяснении. Особенно в случае использования опасных веществ. Нами был проведен эксперимент по обнаружению следов TNT на расстоянии. [1] В данной работе попытаемся смоделировать предыдущий эксперимент и привести теоретическое описание модели.

Мы использовали перестраиваемый CO2 лазер. В основе лежал метод резонансной фототермической спектроскопии [2–7]. Опасное вещество облучалось лазерным излучением. Далее с помощью фотодетектора регистрировался термический сигнал (отклик) от образца. И в конечном итоге сравнивался с эталонным спектром.

Возможность дистанционного обнаружения отдельных микрочастиц ВВ методом резонансной фототермической спектроскопии можно показать, используя стационарную модель нагрева отдельных частиц ВВ, которая реализуется при воздействии на исследуемый объект излучения лазера непрерывного (квазинепрерывного) режима работы.

1. Расчет температуры нагрева

(стационарный случай), (1)

Т — температура, K — теплопроводность, Е — энергия, поглощенная в единице объема в единицу времени;

— интенсивность гауссова пучка; r — радиальная координата; α — коэффициент поглощения; ω — радиус гауссова пучка.

Используя цилиндрическую симметрию задачи нагрева тонкой пленки на полубесконечной подложке, решение уравнение (1) может быть получено с помощью преобразования Фурье-Бесселя:

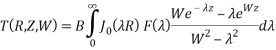, (2)

где R = r/ω, Z = z/ω, W = αω, B = αPL/2πKF(0) — безразмерные параметры и P_L — полная мощность падающего на образец лазерного пучка. Гауссова функция F(R) = , F(λ) — преобразование Бесселя от функции f(r) и J₀ — функция Бесселя нулевого порядка.

Общее решение уравнения (2) для возрастания температуры может быть записано в терминах нормированной функции температуры N (R, Z, W), которая представляет собой понижающий температуру фактор. Тогда выражение для максимального повышения температуры будет иметь вид:

, (3)

где максимальное повышение температуры дается выражением:

. (4)

Будем предполагать, что нагрев ограничивается поверхностным слоем (.

Общее выражение для функцииесть:

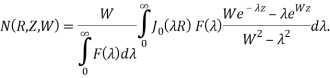(5)

В соответствии с (5) значение температуры вдоль оси лазерного пучка (r = 0) на поверхности образца (z = 0) можно записать в виде:

, (6)

где

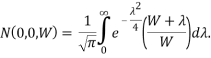(7)

Для больших значений величина

Для большинства веществ коэффициент поглощения велик (обычно > 1000 см^-1) и при диаметре пучка 2ω ~1 см безразмерный параметр имеет большое значение, при котором Поэтому максимальная температура нагрева поверхности равна:

. (8)

2. Расчет мощности теплового излучения

Сначала оценим величину сигнала, соответствующего температуре нагрева

Плотность мощности, испускаемого поверхностью любого тела излучения:

(9)

где — излучательная способность, = 5,67·10–⁸ Вт·м^-2·К^-4 — постоянная Стефана-Больцмана.

Превышение плотности мощности излучаемой нагреваемой частицей по отношению к не подвергающимся нагреву частицам в ее окружении (регистрируемый дифференциальный сигнал):

(10)

Полная мощность излучения, испущенная в телесный угол 4π, равна

,

где А — площадь излучающей поверхности.

Мощность теплового излучения, попадающая в приемную оптическую систему ИК камеры, равна:

, (11)

где — площадь апертуры собирающей линзы, L — расстояние до объекта.

3. Расчет чувствительности метода

— Температура эквивалентная шуму (noise-equivalent temperature difference);

/Фп см·Гц1/2·Вт-1 — удельная обнаружительная способность;

— площадь приемной площадки детектора;

— ширина полосы частот электрического тракта;

Ф_п — пороговый поток приемника (Вт);

NEP — мощность эквивалентная шуму (noise-equivalent power), употребляется для мощности в единичной полосе частот;

Ф_п = NEP = , Вт.

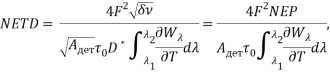(12)

где — диафрагменное число объектива, — фокусное расстояние объектива, - диаметр входной апертуры телескопа, — пропускание оптической системы, — Вт·см^-2·К^-1 (производная мощности излучения по температуре в интервале длин волн ∆λ = λ₂ — λ₁).

Вследствие поглощения возрастание температуры частицы уменьшается экспоненциально с ее размером, т. е. как . Здесь d представляет собой средний размер частиц ВВ (толщину пленки).

Так как размер частицы меньше, чем глубина, на которой поглощается излучение, то формула (8) видоизменится следующим образом:

. (13)

После подстановки (13) в (11) чувствительность метода определим из условия: .

= (14)

Из (12) найдем пороговый поток:

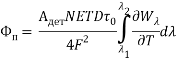. (15)

Приравнивая выражения (14) и (15), а также учитывая, что , получим:

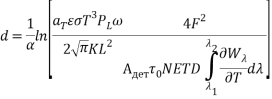. (16)

Для вычисления толщины пленки приведем значения всех параметров, входящих в выражение (16):

α = 5∙ см^-1; 19,6 ( = 5 см); ε = 0,9; Ϭ = 5,67·10–⁸ Вт·м^-2·К^-4 = 5,67·10–¹² Вт·см^-2·К^-4; Т = 300К; Р_L = 1,5·10–² Вт (с учетом 2-х кратного ослабления меандром); ω = 0,5 мм = 5·10–² см; К = 1,55∙10–² Вт·cм^-1·К^-1; L = 50 см; F = 2 ( = 5 см); А_дет = 10–² см² (1 мм х 1 мм); τ₀ = 0,9; NETD = 2,5·10–²К (25 мК); 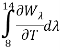= 2,62·10–⁴ Вт·см^-2·К^-1 (∆λ = λ₂ — λ₁ = 14–8). Подставляя приведенные параметры в (16), получим:

d=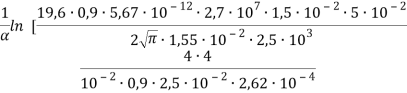] =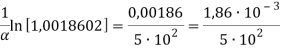≈ 3,7·10–⁶ см = 3,7 мкм.

Тогда чувствительность:

μ = m/S, m=

Учитывая приближенный характер принятой модели, согласие эксперимента с результатами расчета можно считать удовлетворительным.

Из уравнения (14) следует, что

.

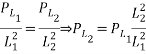Это означает, что для обнаружения следов ВВ такой же концентрации на расстоянии 10 м, средняя мощность излучения лазера должна быть

Так как чувствительность падает обратно пропорционально квадрату расстояния до объекта, то на расстоянии 1 м до объекта описанная система регистрация обеспечивает пороговую чувствительность ~ 25 мкг/см².

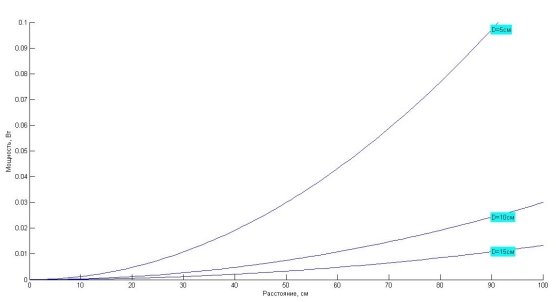
Рис. 1. Расчетные зависимости мощности лазерного излучения от расстояния обнаружения при фиксированной чувствительности (6 мкг/см²) и при разных диаметрах входного окна ИК-объектива

Литература:

1. Лупанов С. В., Головяшкин А. Н. Детектирование микроколичеств твердых опасных веществ на поверхности удаленных объектов // Молодой ученый. — 2017. — №11.
2. Van Neste C. W., Senesac L. R., and Thundat T. Anal.Chem. 81 (5), 1952 (2009).
3. Van Neste C. W., Senesac L. R., Yi D., and Thundat T. Appl. Phys. Lett. 92, 134102 (2008).
4. Van Neste C. W., Senesac L. R., and Thundat T. Appl. Phys. Lett. 92, 234102 (2008).
5. Papantonakis M. R., Kendziora C., Furstenberg R., Stepanowski S. V., Rake M., Stepanowski J., McGill R. A. Proc. SPIE, 7304,730418–9 (2009).
6. Furstenberg R., Kendziora C., Stepanowski S. V., Stepanowski J., Rake M., Papantonakis M. R., Nguyen V, Hubler G. K., and McGill R. A., Appl. Phys. Lett., 93 (22), 224103 (2008).
7. McGill R. A., Kendziora C. A., Furstenberg R., Papantonakis M. R., Horwitz J., and Hubler G. K. U.S. Patent Application 12/255, 103; Field Oct. 21, 2008.