О новейших методах изучения процессов питтинговой коррозии
Авторы: Замалетдинов Ильфат Ибрагимович, Колобова Евгения Алексеевна
Рубрика: Металлургия
Опубликовано в Техника. Технологии. Инженерия №1 (3) январь 2017 г.
Дата публикации: 08.12.2016
Статья просмотрена: 432 раза
Библиографическое описание:
Замалетдинов, И. И. О новейших методах изучения процессов питтинговой коррозии / И. И. Замалетдинов, Е. А. Колобова. — Текст : непосредственный // Техника. Технологии. Инженерия. — 2017. — № 1 (3). — С. 36-45. — URL: https://moluch.ru/th/8/archive/46/1655/ (дата обращения: 25.04.2024).
There are summarizes of current methods for studying pitting (PC), including a method of using neural networks, 3D method for studying the morphology during the growth of pitting, finite element method, ellipsometry method, and others. Get useful information to deepen our understanding of the mechanism and kinetics of growth of pitting corrosion.
Keywords: Pitting corrosion, neural networks, velocity of pitting’s growth
Питтинговая коррозия является опасным видом локального поражения металлов и сплавов, которая, помимо перфорации стенок оболочкового оборудования химических производств, может инициировать процессы коррозионного растрескивания и коррозионной усталости. Поэтому интерес к изучению ПК возрастает в связи с развитием металловедения, с необходимостью создания устойчивых к локальным видам коррозии металлов и сплавов. Прежде чем перейти к новейшим исследованиям в области ПК вкратце охарактеризуем условия возникновения ПК и теоретические представления о ПК, которые базируются на работах научных школ Я. М. Колотыркина [1], И. Л. Розенфельда [2], Н. Д. Томашова [3] и др.
Питтинговая коррозия характерна для пассивирующихся металлов в средах, содержащих в первую очередь галиды (Cl-, Br-, I-) металлов. При достижении критического потенциала питтингообразования ![]() на активных центрах поверхности металла адсорбируются агрессивные анионы и при достижении критической концентрации Скр вызывают растворение в виде соли. Схематически процесс можно представить в виде следующих последовательных стадий [4]:
на активных центрах поверхности металла адсорбируются агрессивные анионы и при достижении критической концентрации Скр вызывают растворение в виде соли. Схематически процесс можно представить в виде следующих последовательных стадий [4]:
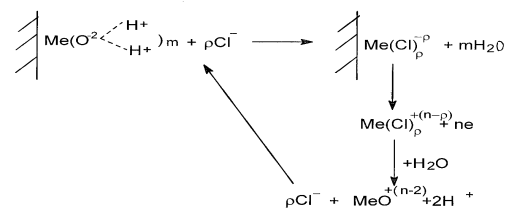
Пассивацию металла вызывают молекулы воды, которые к атому металла обращены кислородным концом. Ионы хлора вытесняют молекулы воды с поверхности и образуют с металлом интермедиаты (комплексы), переходящие в раствор. Далее следует быстрая стадия гидролиза с высвобождением хлор-ионов, вступающих в новое поверхностное взаимодействие с атомами металла. Таким образом формируется циклический или автокаталитический путь реакции питтингообразования [4].
В работе [5] изучали ПК на аэрокосмических сплавах (Al-5,6 Zn-2,5 Mg-1,6 Cu) путем использования искусственных нейронных сетей для моделирования процесса. При этом были использованы оптическая профилометрия и функции Вейбулла для характеристики распределения по глубинам и диаметрам питтингов. Авторы использовали временные эмпирические зависимости скорости роста питтингов, полученные ранее исследователями [6,7]:
![]() ,(1)
,(1)
где t — время, d — глубина или диаметр питтинга, К и b — константы, где b принимает значения от 0,3 до 0,5 [6]. Далее применили трехпараметровую Вейбуловскую функцию распределения для определения популяции питтингов по глубине и диаметру:
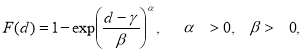 (2)
(2)
где d — глубина питтинга или эквивалентный ей диаметр, α- Вейбуловский параметр формы питтинга, β — параметр масштаба. γ — параметр сдвига (локализации). Методом практической профилометрии установлено, что параметром сдвига можно пренебречь, поэтому выражение (2) авторы [5] упростили:
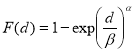 ,(3)
,(3)
где параметры уравнения такие же, что и в уравнении (2). Вейбуловские параметры глубины и диаметра (обозначенные как αгл, βгл, αдиам, βдиам) были использованы в создании искусственных нейронных сети (ИНС). Входами во все НС были показатели температуры, рН, [Cl-], время экспозиции, в то время как выходами были максимальная глубина питтингов, максимальный диаметр питтинга, αгл, βгл, αдиам, βдиам. Каждый параметр, (т. е. температура, глубина питтинга и т. д.) был нормализован между значениями 0 и 1 перед подачей в ИНС. Поскольку температура и величина рН равномерно распределены по их весам, они были нормализованы в соответствии с линейными правилами. Например, температура была нормализована в соответствии с уравнением
![]() ,(4)
,(4)
где Тнорм — нормализованная температура, Ti — температура i -ого опыта, Tmin,, Tmax — минимальная и максимальная температура соответственно. Аналогичной нормализации была подвергнута величина рН, а концентрация хлорида, время, глубина и диаметр питтинга были нормализованы по логарифмической зависимости:
![]() .(5)
.(5)
Нейроносетевое моделирование проводилось с помощью программного обеспечения JMP8. Программное обеспечение позволило выбрать определенный процент данных вначале для тренинга ИНС (67 % было использовано для определения βгл и 90 % для остальных).
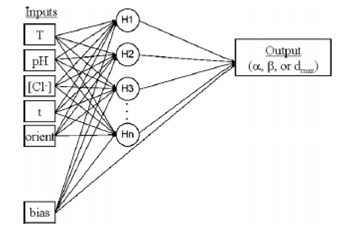
Рис. 1. Нейроносетевая структура для всех конечных параметров (вид параметра, α; параметр шкалы, β; максимальная глубина питтинга или диаметр dmax. Число нод (Нn) в промежуточном слое варьируется для каждого параметра. Входные параметры: температура, рН, концентрация Cl-, время, ориентация (продольная и поперечная) зерен после прокатки, смещение. Выходные параметры α, β или dмакс.
3D — изображение [5], полученное оптической профилометрией представлено на рис. 2.
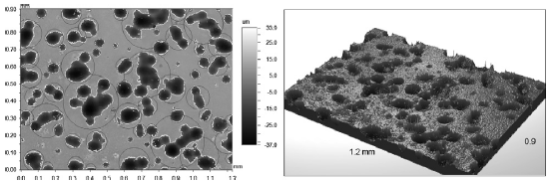
Рис. 2. Слева: Очерченные круговые контуры групп питтингов для съемки на оптическом профилометре сплава алюминия АА 7075 (время испытаний 720 часов при температуре 60оС в растворе 0,6 М хлорида, рН = 6. Справа: 3D изображение образца после испытания
Каждый питтинг был зафиксирован программой в виде круга, пронумерован, расположение и размеры глубин и диаметров были записаны.
В табл. 1 приведено определенное пользователем число узлов (в скрытом слое), использованное для каждой ИНС.
В циклических условиях возникают напряжения, вызывающие рост трещин из глубоких питтингов. Поэтому измеренная действительная максимальная глубина питтингов была сопоставлена с результатами расчета ИНС. Результаты представлены на рис. 3.
Таблица 1
Число нод искусственной нейронной сети при употреблении входящих параметров
|
Параметр |
Число нод |
|
αглубина питтинга |
10 |
|
βглубина питтинга |
10 |
|
αдиаметр питтинга |
10 |
|
βдиаметр питтинга |
9 |
|
Максимальная глубина |
11 |
|
Максимальный диаметр |
12 |
Видно, что данные обучения/проверки ИНС со средним квадратичным отклонением R2 = 0,71 хорошо согласуются с результатами опытов со средним квадратичным отклонением R2 = 0,90. При анализе результатов использования ИНС было установлено, что на максимальную глубину питтингов оказывало влияние время испытаний, температура и рН раствора, а концентрация хлорида и ориентация тонкой структуры после прокатки сплава не оказывало существенного влияния. Незначительное влияние концентрации хлорида объяснено достаточным количеством хлорида для роста питтингов, влияние хлорида возможно возникнет в опытах при более низких концентрациях.
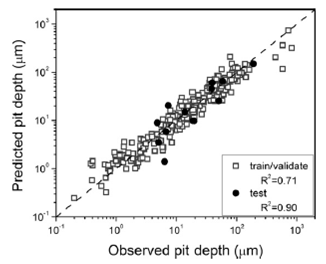
Рис. 3. Действительные максимальные глубины питтингов и рассчитанные ИНС максимальные глубины ложатся на одну прямую [5]
Временные уравнения роста питтингов были получены обученной ИНС: кинетика t1/4 была характерна для щелочных сред и для повышенных температур, а кинетика t1/2 была свойственна для кислых сред и для пониженных температур, однако для многих промежуточных значений рН и температур кинетика была t1/3. Показатель степени от 0,3 до 0,5 для большинства сред соответствовал литературным данным [6,7]. Кроме того, выявленные закономерности кинетики роста питтингов в литературе и результаты предсказаний нейронной сети по величинам степени b делают ей доверие, несмотря на интерполяционный ее характер.
В работе [8] проводились анализы электрохимического шума с использованием временной и частотной зависимостей и статистических параметров потенциала и значений тока, полученные на нержавеющей стали AISI 316 в процессе питтинговой коррозии в деаэрированном 0,5 М растворе NaCl и в процессе коррозионного растрескивания под напряжением в кипящем подкисленном растворе NaCl. Визуальные наблюдения и статистические анализы значений спектрального оценивания тока и потенциала, использующего метод максимальной энтропии, дали полезную информацию на установление различия между этими коррозионными процессами и на влияние напряжения на усиление питтинговой коррозии. Результаты хорошо согласовывались с оптическими микроскопическими наблюдениями.
Исследователи [9] изучали трехмерную питтинговую коррозию, инициированную на включениях MnS стали А537 при циклических нагрузках. При этом использовали софокусный сканирующий лазерный микроскоп с элементным анализом. Ими установлено, что при циклических механических нагрузках питтинги растут анизотропно, т. е. скорости растворения стенок питтинга и дна различаются. Существенно более высокая скорость роста была обнаружена в перпендикулярном направлении оси нагрузок. Конечный элементный анализ указывает на то, что локальная продольная нагрузка играет важную роль на рост питтинга. Кинетика роста питтинга вширь доминировала в продольном направлении. Слияние питтингов в дальнейшем увеличивает скорость роста питтингов, как и предсказывалось методом конечного анализа.
Объектом исследования [9] служила горячекатаная плита из стали А537, которая используется для изготовления нефтяной платформы. Химический состав стали, масс. %: 0,13 С; 1,48 Mn; 0,46 Si; 0,012 P; 0,005 S; 0,04 Cr; 0,19 Ni; 0,05 V; 0,17 Cu; 0,016 Mo, остальное железо. Матрица стали состоит из ферритно-перлитной структуры, полученной при прокатке и коротких поперечных перемещениях, включающей в большом количестве включения MnS в феррите. Статистика измерений показала, что размеры включений MnS в длину составила 27,1 ± 16,4 мкм, в ширину — 2,3 ±0,8 мкм с объемной фракцией 0,24 ± 0,11 % [9].
Испытания на растяжение проводили на универсальной испытательной машине (Shimadzu, модели AG-100KNG) при номинальной скорости деформации 4,2∙10–4 с-1 при комнатной температуре на трех прямоугольных стандартных образцах по направлению прокатки оси нагрузки. Во время испытаний на растяжение деформация записывалась тензометром. Механические свойства были следующие: предел текучести 303±3 МПа, прочность на растяжение 513±1 МПа, относительное удлинение 33±1 %, модуль Юнга (Е) 206±5 ГПа [9].
Образцы гантельной формы с калибровочными размерами длиной и шириной соответственно 15 и 6 мм, и толщиной 6 мм были использованы для тестов на усталостную коррозию. Осевая нагрузка была вдоль направления прокатки. Все образцы были отполированы сначала наждачной бумагой с зернами карбида кремния, затем алмазной пастой на полировочной машине. Коррозионные усталостные испытания проводили на установке Shimadzu, модели ENF-EAS с генератором синусоидальных колебаний с частотой 1 Гц с отношением напряжений 0 при комнатной температуре 20–25 оС. Серия усталостных испытаний проводилась при различных количествах циклов (1×104, 4×104, 7×104, 1×105, 2×105) при напряжении 140 МПа. Было установлено, что коррозионная усталость до разрушения составляла примерно 1×106 циклов. Не было коррозионных трещин в питтингах вплоть до 2×105 циклов, как установлено растровой электронной микроскопией. Поэтому это количество циклов являлось идеальным для исследования влияния циклических напряжений на рост питтингов [9]. Схема установки испытаний на коррозионную усталость представлена на рис. 4.
Из резервуара раствор 3,5 % NaCl со скоростью 20 мл/мин центробежным насосом нагнетался через нижний штуцер в сосуд с образцом, при этом жидкость контактировала с площадкой 1 см2 (остальная поверхность изолировалась силиконовым клеем) узкой части испытуемого образца. Через верхний штуцер жидкость самотеком поступала обратно в резервуар.
После коррозионных испытаний продукты коррозии удаляли раствором этилендиаминотетрауксусной кислотой (готовили 200 мл 1,5 % -ный раствор). Раствор не растворял матрицу и включения MnS.
Морфологию питтингов изучали в продольно-поперечном направлении конфокальным сканирующим лазерным микроскопом (OLYMPUS LEXT OLS3000). Тестировалось более 40 окрестностей вокруг включений MnS. На рис. 5 представлена картина поверхности, на которой форма питтингов была нерегулярной. Поэтому 3D — измерения (длина, ширина и глубина) обсчитывалась программным обеспечением, установленном на OLYMPUS LEXT OLS3000. В случае слияния питтингов их рассматривали как один питтинг.
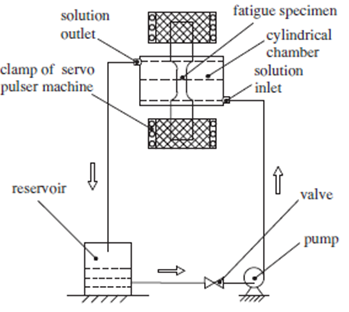
Рис. 4. Схема установки для испытаний на коррозионную усталость
Установлено, что из всех направлений рост в глубину оказался наименьшим после 200 кс испытаний без циклических нагрузок. В условиях циклических нагрузок рост питтинга ускоряется как в ширину, так и в глубину, но со значительным ускорением в ширину. Имеется незначительный рост скорости в длину для циклически напряженных образцов после 100 кс. Явление, по-видимому, связано со слиянием питтингов.


Рис. 5. (а) Поверхность до коррозионных испытаний; (б) питтинги, инициированные после испытаний в растворе 3,5 % NaCl без приложения напряжений

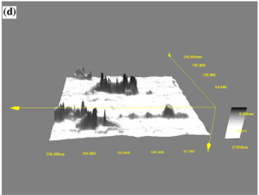
Рис. 5. (с) Питтинги, инициированные после циклических напряжений; (d) 3D — питтинги, снятые софокусным сканирующим микроскопом, обратная картинка с Z фактором 1,5
Кинетику роста питтинга в 3D направлении можно представить в виде уравнения [9]:
![]() , (6)
, (6)
где f(t) представляет ширину, длину и глубину питтингов, a, b, n экспериментальные константы. Константа a представляет инициативный размер питтинга, возникший на включении MnS. Результаты расчетов кинетических параметров [9] представлены в табл.2.
Таблица 2
Сравнение кинетических данных 3D размеров питтингов, полученных без циклических нагрузок ис ними.
|
3D размер |
Амплитуда напряжений, МПа |
α, мкм |
b, мкм∙с-n |
n |
R2 |
|
Ширина |
0 |
3.6±2,7 |
0,20 |
0,32±0,14 |
0,981 |
|
140 |
7,5±0,2 |
1,3∙10–5 |
1,15±0,05 |
0,998 |
|
|
Длина |
0 |
20,4±4,9 |
0,84 |
0,28±0,11 |
0,993 |
|
140 |
31±1,4 |
3,9∙10–3 |
0,72±0,10 |
0,991 |
|
|
Глубина |
0 |
3,4±0,26 |
2,0∙10–4 |
0,76±0,23 |
0,948 |
|
140 |
4,3±0,8 |
1,7∙10–3 |
0.68±0,19 |
0,963 |
Показано, что константа “a” для ширины питтинга была больше, чем усредненный размер включения (т. е. 2,3 мкм). Это объяснено авторами [9] наличием трещины между включением MnS и матрицей (рис. 5(a)). Относительно большие различия, которые найдены для рассчитанной «оригинальной длины» подтверждают, что оригинальная длина питтингов варьируется на различных образцах.
Рассчитанная экспонента n роста питтинга в ширину увеличивалась от 0,32 до 1,15, когда была приложена циклическая нагрузка. Можно сделать сравнение данных табл. 2 и уравнения (6) скорости роста питтинга для образцов, испытанных без напряжений и с напряжением. Например, для после испытаний продолжительностью 200 кс скорости роста в ширину были 16 и 93 пм/с соответственно без нагрузки и с нагрузкой. Результаты свидетельствуют, что скорость роста в ширину может значительно ускоряться при воздействии циклических нагрузок.
В общем, циклические нагрузки усиливают скорость роста питтингов. Питтинги, инициированные на включениях MnS, продемонстрировали анизотропное поведение роста. Скорости роста питтингов в ширину и глубину после воздействия циклических нагрузок были выше, чем скорость роста в длину. Чтобы понять этот феномен рассчитывали методом анализа конечных элементов напряжения вокруг питтингов и их распределение.
Локальные напряжения и распределение напряжений одиночного полуэллипсоидного питтинга были промоделированы методом конечных элементов. Выбраны граничные условия, при которых движение левой стороны модели питтинга фиксировалось вдоль направления х, в то время как движения вдоль направлений y и z были свободными, как показано на рис. 6а. Одноосное растягивающее напряжение 280 МПа (нагрузка от 0 до 280 МПа колебаний с синусоидной волной) была приложена к правой стороне модели. Направление нагрузки было параллельно длинной оси полуэллипсоидного питтинга (направление х на рис. 6а). В соответствии со статистическими результатами типичные длина, ширина и глубина питтингов были 45, 15 и 7,5 мкм соответственно. 3D усредненные напряжения отдельного полуэллипсоидного питтинга показано на рис. 6.
Авторы [10] для изучения процессов ПК сталей 304 и 904L применили метод электрохимической высокочастотной модуляции (ЭВЧМ). Метод заключается в наложении к анодному процессу ПК сигналов возмущения, состоящих из синусоидальных колебаний. Поясняющая схема приведена на рис.7. На корродирующую поверхность подается потенциал, который вырабатывает соответствующий ток (величина тока есть функция потенциала). На нижнем снимке потенциал возмущения состоит из двух синусоидальных волн, наложенных методом ЭВЧМ. В ответ будут получены дополнительные и более высокие частоты, являющиеся нелинейными из-за явлений, протекающие при питтингообразовании. Производится математический анализ токовых сигналов по соответствующим уравнениям для расчета тока коррозии тафелевых наклонов.
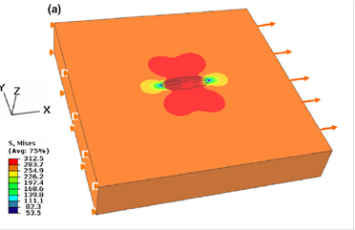
Рис. 6. 3D зоны напряжений вокруг единичного полуэллиптического питтинга (длиной 45 мкм, шириной 15 мкм и глубиной 7,5 мкм). Направление деформации показано стрелками. Зона концентраций согласованных напряжений направлена по оси х. Цветовая гамма с цифрами напряжений приведена слева от рисунка
Соответствующая математическая модель разрабатывалась, чтобы изучить реакцию на возмущение при потенциалах ниже и выше потенциодинамического потенциала питтингообразования. Ставилась цель быстрого нахождения области нелинейного изменения тока с потенциалом. Ток как функция потенциала может определяться по уравнению (7).
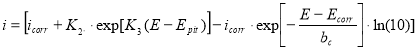 , (7)
, (7)
где icorr — ток коррозии, К2 и К3 — параметры, ассоциируемые с ПК, bc — катодный тафелевский наклон. Здесь Е, Еcorr, Epit — cоответствующие приложенный потенциал, потенциал коррозии и потенциал питтингообразования. Параметры К2 и К3 ассоциируются с ПК и их значения выбираются по уравнению (7) для представления стремительного роста тока с потенциалом, происходящего при инициировании питтинга.
В ЭВЧМ технике авторы [10] применяли возмущающий сигнал потенциала, состоящий из двух синусоидальных волн, как показано ниже
![]() ,(8)
,(8)
где Uo — амплитуда потенциала возмущения, f1 и f2 — частоты возмущения в Гц и Едс — потенциал двойного слоя. Подстановка уравнения (8) в уравнение (7) дает ток во временной области, который может быть затем преобразован в частотной области. Для определения теоретических значений факторов причин ниже потенциала питтингообразования и вблизи потенциала ПО, были выбраны параметры, приведенные в таблице 3.
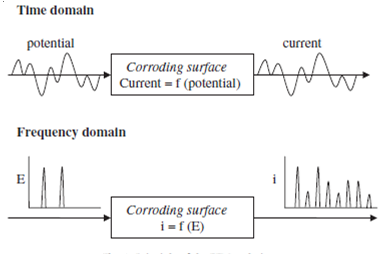
Рис. 7. Верхняя часть временной домен тока как функции потенциала; нижняя часть — частотный домен
Таблица 3
Коррозионные параметры, показывающие свои соответствующие входные значения для симуляции цели
|
Параметр |
Характеристика |
Входные значения |
|
icor |
Ток коррозии |
1 мкА |
|
Epit |
Потенциал питтингообразования |
0,4 В |
|
К2 |
Питтинговый параметр |
1 мкА |
|
К3 |
Нелинейный параметр |
92 мВ-1 |
|
U0 |
Амплитуда потенциала |
10 мВ |
|
bc |
Катодный тафелевский наклон |
120 мВ на декаду |
|
Ecorr |
Потенциал коррозии |
0 В |
|
f1 |
Первая частота |
2 Гц |
|
f2 |
Вторая частота |
5 Гц |
|
Edl |
Потенциал двойного слоя |
-0,3, -0,2…..0,6 |
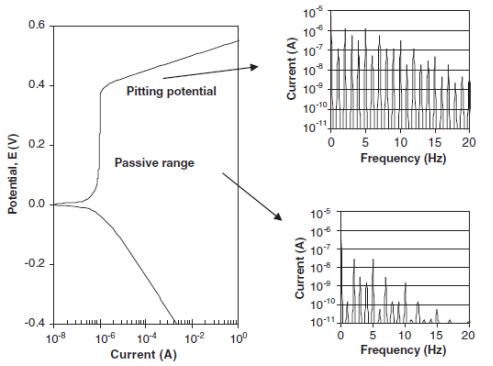
Рис. 8. Поляризационная кривая. Различные нелинейные изменения тока в области роста питтингов и в пассивной области. Потенциал коррозии равен 0 В, а потенциал питтингобразования равен 0,4 В
Видно, что токовые компоненты в области питтинговой коррозии существенно выше, чем токи в пассивной области.
Принимая во внимание данные, полученные с помощью современных методов изучения питтинговой коррозии, можно сделать соответствующие выводы:
- Метод нейронносетевого моделирования позволил выяснить наиболее влиятельные на рост глубины питтингов во время циклических нагрузок входные параметры. Для изучения процесса также использовался метод оптической профилометрии
- В ходе исследования [9] установлен анизотропный характер роста питтингов при циклических механических нагрузках. В период приложения нагрузки, экспонента n роста питтингов в ширину возрастала более чем в 2 раза, что свидетельствует о воздействии циклической нагрузки на скорость роста в ширину
- При приложении одноосного растягивающего напряжения к полу-эллипсообразному питтингу, напряжения, возникающие перпендикулярно оси растяжения, превышают значение приложенной нагрузки, увеличивая скорость роста ПК в ширину и глубину
- Метод электрохимической высокочастотной модуляции позволяет отследить инициирование роста питтинга, в связи со стремительным ростом силы тока и потенциала в этот период.
Литература:
- Колотыркин Я. М. Металл и коррозия. М.: Металлургия, 1985. — 88 с.
- Розенфельд И. Л. Ингибиторы коррозии. Монография. — М.: Химия, 1977. — 352 с.: ил.
- Томашов Н. Д. Коррозия металлов с кислородной деполяризацией. Учебник: — М., Л.: Издательство АН СССР, 1947. — 250 с.
- Розенфельд И. Л. Ускоренные методы коррозионных испытаний металлов (теория и практика)/ И. Л. Розенфельд, К. А. Жигалова. М.: Металлургия, 1966. — 348с.
- Modeling the environmental dependence of pit growth using neural network approaches/ M. K. Cavanaugh, R. G. Buchheit, N. Birbilis//Corrosion Science, Vol.52 (2010), p.3070–3077.
- Pitting corrosion of aluminium/ Z. Szklarska-Smialowska// Corrosion Science, Vol. 41 (1999), p.1743–1767.
- A simplified method for estimating corrosion cavity growth rates/ G Engelhardt, M Urquidi-Macdonald, DD Macdonald// Corrosion Science,Vol.39 (1997), p.419–441.
- Assessment of stress corrosion crack initiation and propagation in AISI type 316 stainless steel by electrochemical noise technique/ T. Anita, M. G. Pujar, H. Shaikh, R. K. Dayal, H. S. Khatak// Corrosion Science, Vol.48, Issue 9, September 2006, p.2689–2710.
- Anisotropic 3D growth of corrosion pits initiated at MnS inclusions for A537 steel during corrosion fatigue/ Jin Ma, Bo Zhang, Jianqiu Wang, Guozhen Wang, En-Hou Han, Wei Ke //Corrosion Science, Vol.52 (2010), p.2867–2877.
- Evolution of current transients and morphology of metastable and stable pitting on stainless steel near the critical pitting temperature/ M. H. Moayed, R. C. Newman// Corrosion Science, Vol.48, Issue 4, April 2006, p.1004–1018.
Похожие статьи
Бесконтактные методы контроля толщины стенки изделия...
Скорость контроля до 500 мм/с. Максимальная контролируемая толщина металла составляет 15 мм, при допустимой толщине
Это уменьшение пропорционально глубине дефекта, а минимальное значение Вх соответствует максимальной глубине дефекта [7,8].
Критерии оценки многоцикловой механической выносливости при...
Нагрузки и деформации, при которых обычно происходит усталостное разрушение, намного ниже тех
Расчет на усталость винта с упорной резьбой в программной...
По выполненным измерениям выявляют слои, внесшие наибольший вклад в глубину колеи, появившейся на...
Обзор существующих методик расчёта основных параметров...
Bk — ширина катка, (м); φ0 — угол захвата материала катком, (рад); H0 упл — исходная толщина уплотняемого слоя, (м).
x — глубина распределения давления по фильере, (м)
В связи с интенсификацией эксплуатационных процессов, увеличением скоростей...
Выбор конструкционных материалов для оборудования установки...
С ростом температуры коррозионная агрессивность растворов ДЭГ увеличивается и достигается. При этом скорость коррозии в паровой фазе растворов ДЭГ выше скорости коррозии в жидкой фазе, что связано с переходом в нее легколетучих органических кислот...
Нагрузки от подвижного состава, действующие на подпорную стену
Рис. 3. Учет увеличения нагрузки при повышенном уровне грунтовых вод.
Ширина полосы а принимается а = 2,7 + 2 • Нб, (Нб — толщина балластного слоя под подошвой шпалы, принимается равной 0,75 м, а при отсутствии балластного слоя Нб = 0).
Опыт модификации конструкции антенного сооружения
где – характерная скорость ветра; – высота характерной скорости ветра; – параметр шероховатости поверхности в месте установки сооружения.
где – растягивающая сила; b – ширина полосы; a – длина трещины; w – толщина полки.
Методика определения энерготехнологических параметров...
По изложенной выше методике также были проведены расчеты энергетических параметров УКПА-2,4 при глубоком рыхлении почвы (7 рабочих органов, установочная глубина обработки , рабочие органы установлены в 2 ряда, угол крошения 300, угол установки стойки рабочих...
О дискретизации нормального сечения железобетонного элемента...
Приведены указания по трансформации выражений, определяющих жесткостные характеристики сечения при переменных деформативных параметрах бетона.
Если по глубине сечения, нормального к продольной оси элемента, установить закономерности...
Похожие статьи
Бесконтактные методы контроля толщины стенки изделия...
Скорость контроля до 500 мм/с. Максимальная контролируемая толщина металла составляет 15 мм, при допустимой толщине
Это уменьшение пропорционально глубине дефекта, а минимальное значение Вх соответствует максимальной глубине дефекта [7,8].
Критерии оценки многоцикловой механической выносливости при...
Нагрузки и деформации, при которых обычно происходит усталостное разрушение, намного ниже тех
Расчет на усталость винта с упорной резьбой в программной...
По выполненным измерениям выявляют слои, внесшие наибольший вклад в глубину колеи, появившейся на...
Обзор существующих методик расчёта основных параметров...
Bk — ширина катка, (м); φ0 — угол захвата материала катком, (рад); H0 упл — исходная толщина уплотняемого слоя, (м).
x — глубина распределения давления по фильере, (м)
В связи с интенсификацией эксплуатационных процессов, увеличением скоростей...
Выбор конструкционных материалов для оборудования установки...
С ростом температуры коррозионная агрессивность растворов ДЭГ увеличивается и достигается. При этом скорость коррозии в паровой фазе растворов ДЭГ выше скорости коррозии в жидкой фазе, что связано с переходом в нее легколетучих органических кислот...
Нагрузки от подвижного состава, действующие на подпорную стену
Рис. 3. Учет увеличения нагрузки при повышенном уровне грунтовых вод.
Ширина полосы а принимается а = 2,7 + 2 • Нб, (Нб — толщина балластного слоя под подошвой шпалы, принимается равной 0,75 м, а при отсутствии балластного слоя Нб = 0).
Опыт модификации конструкции антенного сооружения
где – характерная скорость ветра; – высота характерной скорости ветра; – параметр шероховатости поверхности в месте установки сооружения.
где – растягивающая сила; b – ширина полосы; a – длина трещины; w – толщина полки.
Методика определения энерготехнологических параметров...
По изложенной выше методике также были проведены расчеты энергетических параметров УКПА-2,4 при глубоком рыхлении почвы (7 рабочих органов, установочная глубина обработки , рабочие органы установлены в 2 ряда, угол крошения 300, угол установки стойки рабочих...
О дискретизации нормального сечения железобетонного элемента...
Приведены указания по трансформации выражений, определяющих жесткостные характеристики сечения при переменных деформативных параметрах бетона.
Если по глубине сечения, нормального к продольной оси элемента, установить закономерности...







