При представлении современных систем автоматического управления в виде структурных схем они становятся громоздкими и нечитаемыми, а их исследование требует большого количества сложных для человека расчетов. К тому же, многие студенты, обучающиеся по направлению «Автоматизация технологических процессов и производств» не понимают современных методов расчета передаточных функций систем управления. В данной статье рассмотрен способ представления структурных схем в виде ориентированных графов, что сильно упрощает читабельность схем, а также дает возможность написания алгоритмов обработки систем автоматического управления, представленных в виде графов. В статье предложены алгоритмы для нахождения передаточных функций, написанные на языке программирования C#, которые могут стать базой для собственной программы для исследования САУ, а также студентами для проверки корректности найденной передаточной функции.

Ключевые слова: граф, орграф, теория автоматического управления, система автоматического управления, передаточная функция.

Для исследования систем автоматического управления в ТАУ их принято схематично изображать в виде структурных схем, на которых располагают элементы, выполняющие функции, необходимые для осуществления процесса автоматического управления [1] [2].

Однако, на практике схемы становятся слишком громоздкими и сложными для восприятия. К тому же, исследование САУ требует большого количества сложных для человека расчетов.

Использование вычислительных ресурсов компьютера упрощает задачу исследования систем автоматического управления [3]. Однако, структурное описание схемы, как типа данных для ЭВМ и алгоритмов работы с ними является трудоемким процессом.

Представление схем в виде ориентированных графов, решает все выше поставленные проблемы:

1) Делает схему проще и читабельнее;

2) Орграф легко представить как тип данных;

3) Существует множество алгоритмов для работы с графами [4].

Для преобразования структурной схемы в ориентированный граф все звенья и сумматоры заменяют на вершины графа, а дуги, которые их соединяют, имеют направление распространения сигнала и характеризуются передаточной функцией [5] [6].

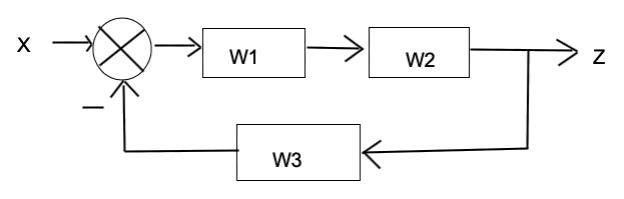
Рис. 1. Структурная схема САУ

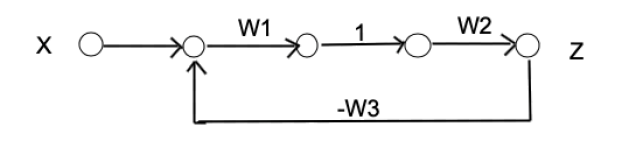
Рис. 2. Схема САУ, преобразованная в орграф

После преобразования схемы в орграф для исследования САУ необходимо найти передаточную функцию всей системы. Для ее нахождения можно использовать правило некасающихся контуров:

W(s) = Y(s)/X(s) = (1)

где Wпрi — передаточная функция i-го отдельного прямого пути от X(s) до Y(s), вычисленная как произведение передаточных функций дуг, входящих в этот путь;

∆s — определитель орграфа [7] [8].

(2)

Wj(s) — передаточная функция j-го замкнутого контура, вычисленная как произведение передаточных функций дуг, входящих в этот контур;

Wj(s)Wk(s) — произведение передаточных функций пары (j-го и k-го) замкнутых контуров, не касающихся ни дугами, ни вершинами, суммирование осуществляется по всем парам некасающихся контуров;

- определитель орграфа, полученного при удалении дуг и вершин i-го отдельного прямого пути, определяется по формуле (2).

Исходя из формулы, для нахождения передаточной функции нужно в первую очередь найти все прямые пути от вершины, которая соответствует входному сигналу до вершины, соответствующей выходному сигналу точки, причем, ни одна вершина в пути не должна повторяться, а также найти все замкнутые контуры.

В качестве примера рассчитаем передаточную функцию схемы приведенной на рисунке 3.

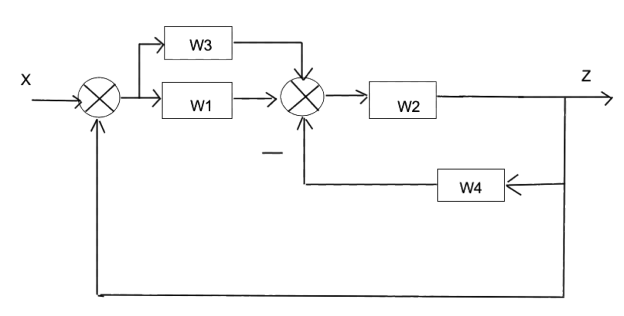
Рис. 3. Пример структурной схемы САУ

Преобразуя данную схему в ориентированных граф, используя правила указанные выше, получим орграф следующего вида:

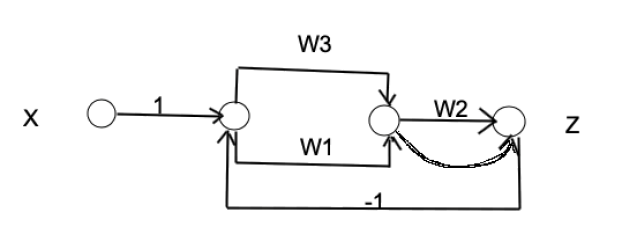
Рис. 4. Пример преобразования структурной схемы САУ в орграф

По правилу замкнутых контуров найдем передаточные функции прямых путей, а затем замкнутых контуров:

Прямые пути:

А) W₂W₃

Б) W₂W₁

Замкнутые контуры:

А) — W₂W₃

Б) — W₂W₁

В) -W₂W₄

Все замкнутые контуры имеют общую дугу W₂, следственно некасающиеся контуры отсутствуют, а определить орграфа имеет следующий вид:

W₂W₃ + W₂W₁ + W₂W₄, а передаточная функция всей системы:

W =

Данный метод может быть использован студентами, изучающих теорию автоматического управления, для ручного расчета простых структурных схем автоматического управления.

Для сложных производственных схем будем использовать ресурсы компьютера. Для достижения этой цели нужно выполнить следующие задачи:

1) Представим ориентированный граф в удобном для обработки компьютером виде

2) Опишем алгоритм поиска прямых путей графа

3) Опишем алгоритм поиска замкнутых контуров графа [5].

Для работы с графом представляем его в удобном для обработки виде и реализуем три класса:

1) Класс для хранения пройденных вершин

2) Класс для хранения стека пути

3) Класс для хранения вершин, которые мы можем посетить из текущей, но еще не посетили.

Реализация всех классов и методов, представленных в статье, осуществлялась на языке программирования c# в среде разработки Visual Studio [9] [10].

Для работы с графом реализуем класс Edge, представляющий его вершину, а также класс Neighbor для хранения списка соседних вершин и значения передаточной функции между ними. Пример реализации метода Edge представлен на рисунке 5.

Рис. 5. Реализация класса Edge

В текущей реализации класс Edge каждой вершине класс создается уникальный идентификатор, а также реализован метод для добавления соседних вершин графа и назначение им передаточной функции, метод для получения всех соседних вершин и метод для получения значений передаточных функций между текущей и переданной на вход вершиной.

Для представления соседей реализован класс Neighbor, который хранит в себе вершину соседа и значения передаточной функции между текущей вершиной и ее соседом. Пример его реализации представлен на рисунке 6.

Рис. 6. Реализация класса Neighbor

Первый класс History, необходимый для работы с графом, имеет поле для хранения пройденных вершин графа и методов, с помощью которых можно проверять была ли посещена текущая вершина, а также менять состояние посещения на противоположное. Реализация данного класса может иметь следующий вид:

Рис. 7. Реализация класса History

В текущей реализации класс History имеет публичное поле VisitedEdges, которое представляет собой словарь, ключи которого — вершины графа, а значение является булевой величиной и показывает, была ли посещена текущая вершина (true — посещена, false — не посещена).

Конструктор представленного класс принимает на вход сам граф, представленный перечислением вершин, преобразует его в словарь и запоминает в поле VisitedEdges, устанавливая всем вершинам значение false, так как ни одна вершина еще не была посещена.

Внутри класса реализованы три вспомогательных метода IsVisited, VisitedEdges, SetUnvisited, каждый из которых принимает на вход вершину. Первый метод возвращает для текущей вершины булевое значение, которое показывает была ли она посещена, второй устанавливает вершине значение того, что она была посещена, а третий то, что вершина не была посещена.

Второй класс содержит поле для хранения стека пройденного пути, а также методы для получения текущего стека, добавления в него новой вершины, удаления из него вершины и тд. Пример реализация такого класса представлен на рисунке 8.

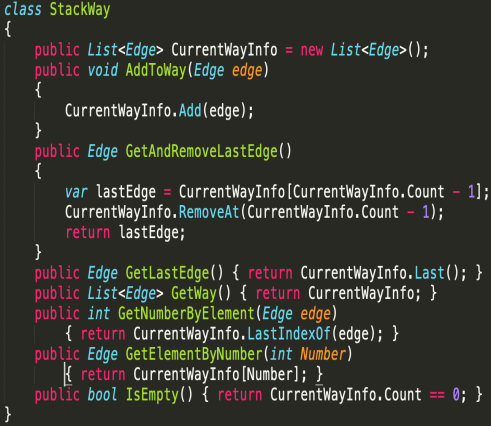
Рис. 8. Реализация класса StackWay

Класс StackWay в текущей реализации содержит список вершин CurrentWayInfo, который служит для хранения самого стека пути, а также несколько вспомогательных методов для добавления новой вершины в стек, для удаления вершины из стека, получения последней вершины, индекса вершины и получения вершины по индексу, проверки стека на пустоту.

Третий класс служит того, чтобы на этапе обработки текущей вершины хранить информацию о том, из какой вершины мы попали в текущую, и какие можем посетить, но еще не посещали. Класс должен содержать словарь, ключами которого являются вершины, а значения — списка вершин, которые можно посетить из текущей.

Рис. 9. Реализация класса ChildDependecy

Представленный класс ChildDependecy в текущей реализации имеет публичное поле childDependecy, который является словарем и в качестве ключа хранит вершину, а в качестве значения — список ее вершин-детей. Конструктор такого класса принимает на вход в качестве аргумента весь граф, предоставленный как перечисление вершин, превращает его в словарь, ключи которого вершины, а значения — пустые списки, и запоминает его в поле childDependecy.

В текущем классе реализованы вспомогательные методы для получения всех зависимостей текущей вершины, для добавления к вершине новых зависимостей и для установки всем зависимостям вершины состояние «непосещенности».

Реализуем метод поиска всех простых путей графа между двумя заданными вершинами, который принимает на вход два параметра: начальную и конечную вершины, а возвращает список путей. Реализация метода может иметь следующий вид:

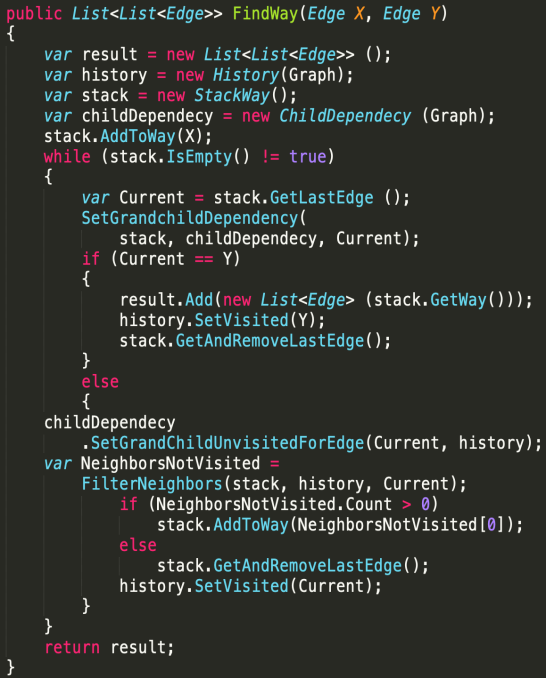
Рис. 10. Реализация метода FindWay

Метод FindWay возвращает все наборы вершин от переданной ему вершины Х до вершины У. В его реализации был также использован вспомогательный метод FilterNeighbors, который позволяет получить список непосещенных вершин-соседей переданной в него вершины.

Рис. 11. Реализация метода FilterNeighbors

Замкнутые контуры являются так же простыми путями, где начальная и конечная вершины совпадают, поэтому для их поиска можно также воспользоваться методом FindWay(Edge X, Edge Y). Однако его следует немного модифицировать, чтобы не вылетать из метода при первой итерации. Для этого достаточно добавить булевую переменную, благодаря которой будет определяться первая итерация для пропуска проверки if (Current == Y), а в конце ее значение будет меняться на противоположное. А если передавать в метод FindWay вместо самой вершины ее соседей и в получившиеся наборы вершин в начало вставить нужную нам вершину, то мы получим все замкнутые в нее пути, не модернизируя метод.

После нахождения всех простых путей и замкнутых контуров достаточно подставить получившиеся значения передаточных функций в формулу 1 для нахождения передаточной функции всей системы. Для ее вычисление следует реализовать отдельный метод.

Из полученного набора вершин методом FindWay можно найти передаточные функции, воспользовавшись методом GetFunctionsBetweenNeaighbor, реализованном в классе Edge. Однако, учитывая то, что между двумя одинаковыми вершинами может быть более одного пути, нужно посчитать декартово произведение списков передаточных функций между вершинами. Реализация такого участка кода представлен на рисунке 12, где метод CartesianProducts реализует декартово произведение.

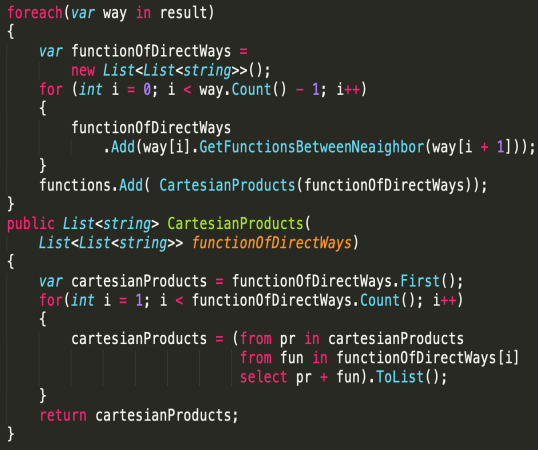
Рис. 12. Поиск передаточных функций и реализация метода CartesianProducts

Приведенные в статье алгоритмы могут использоваться студентами, обучающимися по направлению АТПП, для ручного расчета передаточных функций и исследования простых систем управления, а также стать основой программ для проверки расчетов передаточных функций или основой собственной системы исследования автоматических система управления.

Литература:

1. Способ преобразования структурных схем систем автоматического управления при помощи графов scienceforum.ru/2017/article2017036315. (Дата обращения: 15.10.19).
2. Целигорова E. H. Современные информационные технологии и их использование для исследования систем автоматического управления// Инженерный вестник Дона, 2010, № 3 URL: ivdon.ru/magazine/archive/n3y2013/1907.
3. Гинис Л. А. Развитие инструментария когнитивного моделирования для исследования сложных систем// Инженерный вестник Дона, 2013, № 3 URL: ivdon.ru/ru/magazine/archive/n3y2013/1806.
4. Ориентированные графы систем автоматического управления drive.ispu.ru/elib/lebedev/8.html. (Дата обращения: 23.10.19).
5. Шестаков В. М., Нагибина О. Л., Томчина О. П. Практикум по теории автоматического управления. 2–5 сс.
6. Ерофеев А. А. Теория автоматического управления. 120–130с.
7. Bondy, J. A.; Murty, U. S. R. (2008). Graph Theory. Springer. 10–30 pp.
8. Kepner, Jeremy; Gilbert, John (2011). Graph Algorithms in The Language of Linear Algebra. 5p.
9. Visual Studio visualstudio.microsoft.com. (Дата обращения: 17.10.19).
10. Документация по c# docs.microsoft.com/ru-ru/dotnet/csharp. (Дата обращения: 18.10.19).