Основой большинства анимация является интерполяция значений. Одним из самых простых примеров анимации является интерполяция положения точки в пространстве. Но даже сделать это правильно нетривиально и требует некоторого обсуждения нескольких вопросов: соответствующая интерполяционная функция; параметризация функции на основе пройденного расстояния; и поддержание желаемого контроля интерполированной позиции во времени.

Большая часть этого обсуждения будет касаться интерполяции пространственных значений. Читатель должен помнить, что любое изменяемое значение, участвующее в процессе анимации (и отображения), такое как прозрачность объекта, фокусное расстояние камеры или цвет источника света, может со временем подвергаться интерполяции. Часто аниматор имеет список значений, связанных с данным параметром в определенных кадрах (называемых ключевыми кадрами или крайностями) анимации. Вопрос, на который нужно ответить, заключается в том, как лучше всего сгенерировать значения параметра для кадров между ключевыми кадрами. Параметр, который должен быть интерполирован, может быть координатой положения объекта, общим углом придатка робота, атрибутом прозрачности объекта или любым другим параметром, используемым для манипулирования и отображения элементов компьютерной графики. В любом случае, значения для интересующего параметра должны быть сгенерированы для всех кадров между ключевыми кадрами.

Например, если аниматор хочет, чтобы позиция объекта была (-5, 0, 0) в кадре 22, а позиция была (5, 0, 0) в кадре 67, то необходимо сгенерировать значения для позиции для кадров с 23 по 66. Можно использовать линейную интерполяцию. Но что, если объект должен казаться остановленным в кадре 22 и должен ускоряться из этой позиции, достигать максимальной скорости в кадре 34, начинать замедляться в кадре 50 и останавливаться в кадре 67? Или, возможно, вместо остановки в кадре67, объект должен продолжать положение (5, 10, 0) и достичь там в кадре 80 по хорошему изогнутому пути? В следующих нескольких разделах рассматриваются вопросы генерации точек вдоль пути, заданного контрольными точками, и распределения точек вдоль пути в соответствии с соображениями синхронизации.

Интерполяция иаппроксимация

При заданном наборе точек для описания кривой одно из первых решений, которое необходимо принять, заключается в том, представляют ли данные значения фактические положения, через которые должна пройти кривая (интерполяция), или они предназначены просто для управления формой кривой и не представляют фактические положения, которые кривая будет пересекать (приближение). См. Рисунок 1. Это различие обычно зависит от того, являются ли точки данных точками выборки желаемой кривой или используются ли они для построения новой кривой. В первом случае предполагается, что искомая кривая ограничена для перемещения через точки выборки, что, конечно, является определением интерполирующего сплайна. В последнем случае можно использовать аппроксимирующий сплайн, поскольку аниматор быстро получает представление о том, как изменение положения контрольных точек влияет на форму кривой.

В обзорах М. Мортенсена обычно используются интерполяционные функции — формулировка Эрмита и сплайн Катмулла-Рома. Формулировка Эрмита требует информации о касательной в конечных точках, тогда как Catmull-Rom использует только те положения, через которые должна пройти кривая. Функции, которые аппроксимируют некоторую или всю управляющую информацию, включают кривые Безье и B-сплайна [1].

Сложность

Сложность лежащего в основе уравнения интерполяции вызывает беспокойство, поскольку это приводит к его вычислительной эффективности. Чем проще основные уравнения интерполирующей функции, тем быстрее ее оценка. На практике полиномы легко вычислить, и кубические полиномы являются полиномами самого низкого порядка, которые обеспечивают достаточную гладкость, но при этом обеспечивают достаточную гибкость для удовлетворения других ограничений, таких как начальные и конечные позиции и касательные. Полином, порядок которого меньше кубического, не обеспечивает точки перегиба между двумя конечными точками и, следовательно, может не соответствовать гладко определенным точкам данных. Использование полинома, порядок которого выше кубического, обычно не дает каких-либо существенных преимуществ и является более дорогостоящим для оценки.

Непрерывность

Гладкость полученной кривой является основным фактором. Математически гладкость определяется тем, сколько производных уравнения кривой являются непрерывными. Непрерывность нулевого порядка относится к непрерывности значений самой кривой. Делает ли кривая прерывистые скачки в своих значениях?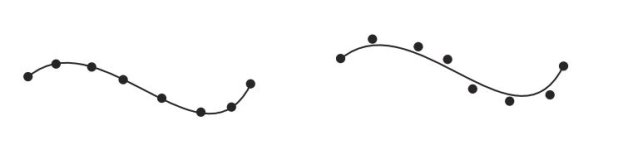

Рис. 1. Сравнение интерполяции и аппроксимирующих сплайнов

Если небольшое изменение значения параметра всегда приводит к небольшому изменению значения функции, то кривая имеет нулевой порядок или позиционную непрерывность. Если то же самое можно сказать о первой производной функции (мгновенном изменении значений кривой), то функция имеет непрерывность первого порядка или тангенциальную. Непрерывность второго порядка относится к непрерывной кривизне или мгновенному изменению вектора касательной. См. Рисунок 2. В некоторых средах с геометрическим дизайном

Может потребоваться непрерывность кривых и поверхностей второго порядка, но в большинстве анимационных приложений непрерывность первого порядка достаточна.

В большинстве приложений кривая является составной; он состоит из нескольких сегментов. Тогда возникает проблема не в непрерывности сегмента (который в случае многочленов имеет бесконечный порядок), а в непрерывности, реализуемой на стыке между соседними сегментами. Согласно Д. Роджерсу и Дж. Адамсу, кривые Эрмита, Кэтмулла Рома, параболическое смешивание и кубическая кривая Безье могут создавать непрерывность первого порядка между сегментами кривой. Существует форма составных кривых Эрмита, которая создает непрерывность второго порядка между сегментами за счет местного управления. Кубический B-сплайн всюду непрерывен второго порядка. Все эти кривые обеспечивают достаточную непрерывность для большинства анимационных приложений [2].

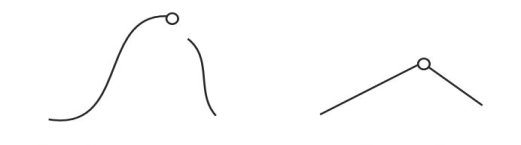
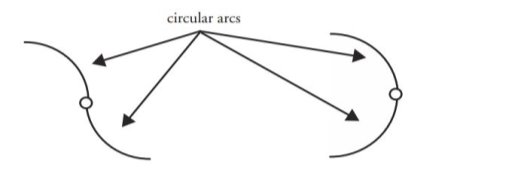
Рис. 2. Непрерывность (в точке, обозначенной маленьким кружком). Глобальное против местного управления

При разработке кривой пользователь часто перемещает одну или несколько точек которые управляют формой кривой, чтобы настроить только часть кривой. Обычно считается преимуществом, если изменение в одной контрольной точке влияет только на ограниченную область кривой, а не на изменение всей кривой. Формулировка, в которой контрольные точки оказывают ограниченное влияние на кривую, называется местным контролем. Если перемещение одной контрольной точки переопределяет всю кривую, хотя и незначительно, то формулировка обеспечивает глобальный контроль. См. Рисунок 3. Местное управление почти всегда рассматривается как наиболее желательное из двух.

Почти все составные кривые обеспечивают локальное управление: параболическое смешивание, сплайны Кэтмулла-Рома, составной кубический Безье и кубический B-сплайн. Форма кривых Эрмита, которая обеспечивает непрерывность второго порядка на стыках сегментов, делает это за счет локального управления. Кривые Безье и B-сплайна более высокого порядка имеют менее локализованный контроль, чем их кубические формы.

Заключение

Существует много формулировок, которые можно использовать для интерполяции значений. Выбор конкретной формулировки зависит от желаемой преемственности, от того, требуется ли локальное управление, от степени сложности вычислений и от информации, требуемой от пользователя.

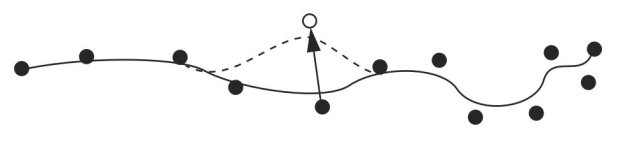
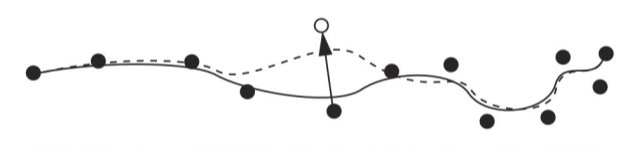
Рис. 3 Сравнение локального и глобального эффекта перемещения контрольной точки

По мнению М. Мортенсена, сплайн Catmull-Rom часто используется в анимации движения траектории, потому что он является интерполяционным сплайном и не требует никакой дополнительной информации от пользователя, кроме точек, через которые должен пройти путь. Кривые Безье, которые вынуждены проходить через заданные точки, также часто используются. Параболическое смешивание — часто пропускаемая техника, которая также обеспечивает местный контроль и является интерполяционной. [3]

В этом случае мы можем видеть, что если одна из контрольных точек изменяется, вся кривая может измениться в глобальном контроле. Однако в локальном контроле все иначе: если одна из точек изменена, она воздействует на две точки, которые находятся рядом с изменяющимися точками.

Литература:

1. M.Mortensen, Geometric Modeling, John wiley and Sons, New York, 1985.
2. D.Rogers and J.Adams, Mathematical Elements for Computer Graphics, Mc-Graw-Hill, New York, 1976
3. D. Kochanek, “Interpolating Splines with Local Tension, Continuity and Bias Control,” Computer Graphics (Proceedings of SIGGRAPH 84), (July 1984, Minneapolis, Minn.).