В рассматриваемых используя методы характеристики и распространяющихся волн, решена краевая задача о собственных и параметрических колебаниях, о взаимодействии изолированной волны с неподвижными опорами гибкого элемента. Сравнение решение задачи распространения волны в бегущем элементе с классическим случаем неподвижного элемента показывает существенные отличия в характере отражения волн.

Можно привести множество примеров, когда металлические и гибкие трубопроводы, шланги и т. д. при работе бурильных установок подвергаются достаточно большим внутренним давлениям воздуха, жидкости и других включений. Например, насосы для промывки скважин перекачивают воду, соляные и глинистые растворы с различными добавками. Забор жидкости (всасывание) обычно осуществляется из открытых резервуаров, расположенных ниже насоса. При заборе жидкости во всасывающей магистрали создается разрежение, и жидкость, преодолевая внутреннее давление и сопротивление во всасывающей магистрали, поднимается в камеру всасывания насоса.

Различные насосы способны подавать давление от 10 до 100 ат. Например, плунжерные насосы производительностью до 22–30 л/мин (насосы марки НПГ-1) и производительностью до 75 л/мин (насосы марки НА-75/25) могут подавать давление до 15 ат, а поршневые насосы производительностью 360–1000 л/мин (насосы марки 9МГР) могут подавать давление от 35 до 100 ат.

При работе бурильных установок в различных средах, движущихся внутри полых цилиндрических волноводов — гибких и металлических трубопроводов, возникают волны давления и могут возникать волны разрежения.

Для наглядности распространения волн давления и разрежение рассмотрим следующий пример движения двух несмешивающихся жидкостей в тонком гибком цилиндре (рис. 1). Пусть при области гибкого элемента с радиусами и заполнены одной, а область с радиусом другой несмешивающихся жидкостями. На границах между этими жидкостями имеется воздух — участки с радиусами . Если при внешнее давление, подаваемое в гибкий элемент отсутствует или имеет номинальные значения, то . Допустим, что в некоторый момент времени внутреннее давление достигает максимальное (критическое) значение и поперечные сечения приобретают, например, изображенную на рис. 1 форму. Если при жидкости начнут мгновенно двигаться, то принятая в момент времени форма поперечных сечений будет перемещаться (распространяться) вдоль оси до конца гибкого элемента.

Аналогичный пример движения двух или нескольких видов несмешивающихся жидкостей можно наблюдать при перемещении их по стеклянной пробирке (рис. 2).

Рис. 1

Рис. 2

Рассмотренные примеры движения возникают внутри полых волноводов под действием внутренних давлений.

Под действием других видов внешних механических нагрузок в гибких элементах возникают совсем иного характера волновые процессы и бегущие волны.

Чтобы наглядно представить понятие бегущей волны рассмотрим пример передвижение садовой гусеницы [1–2] по горизонтальной плоскости x (рис. 3).

Предположим, что за время t гусеница проходит путь равное по величине x. Передвижение гусеницы условно разобьем на следующие пять положения.

В положении I гусеница находится в покое на горизонтальной поверхности.

В положении II гусеница начала передвигаться в сторону роста оси x, в ее хвостовой части (точка 0) возникла изогнутая участок — бегущая волнараспространяющаяся вдоль гусеницы со скоростью .

В положении III бегущая волна продолжает передвигаться вдоль гусеницы со скоростью .

В положении IV наступает момент, когда головное сечение гусеницы начнет двигаться вдоль оси x со скоростью .

В положении V головное сечение передвинулась на расстояние

x = t.

Таким образом, тело гусеницы элементарной массой за время переместилось на расстояние .

Последний пример является лишь наглядным представлением перемещение тело гусеницы и не имеет ничего общего с динамическими явлениями, возникающими в гибких элементах.

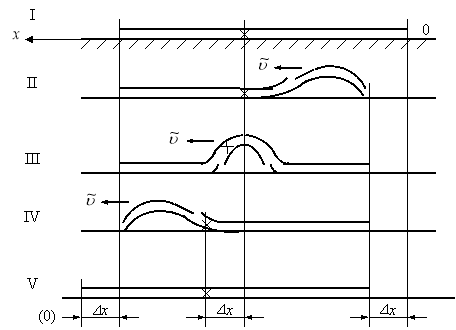
Рис. 3

Литература:

1. Мамасаидов М. Т.,Эргашов М., Тавбаев Ж. С. Прочность гибких элементов и трубопроводов бурильных установок. Бишкек: Илим, 2001.-252 с.
2. Тавбаев Ж. С. Распрастранение бегущей волны в нити.//Вкн.«Свойства и взаимодействия волн в нитей» Фан.Ташкеент.2001 г. С.41–60.