Разработка алгоритма эффективного кодирования на основе неравенства Крафта



Эффективное кодирование применяется для уменьшения объема занимаемого данными для хранения информации и с целью сокращения времени передачи информации. Разработаны новые алгоритмы эффективного кодирования и декодирования информации на основе неравенства Крафта и алгоритм эффективной упаковки, экспериментально подтверждена эффективность предложенного метода. Разработанный алгоритм эффективной упаковки на основе неравенства Крафта был протестирован еще на 9 различных вариантах текстовых данных, и во всех случаях показал оптимальный результат.

Ключевые слова: информация, кодирование, неравенство Крафта, сжатие, эффективное кодирование.

Effective coding is used to reduce the amount of data used for storing information and in order to reduce the transmission time of information. New effective encoding and decoding information algorithms based on Kraft's inequality and effective packing algorithm have been developed. Experimentally confirmed the efficiency of the proposed method. The developed effective packing algorithm based on Kraft's inequality was tested on 9 different variants of text data, and in all cases showed the optimal result.

Keywords: information, coding, Kraft–McMillan inequality, data compression, effectively coding, prefix code

Введение

Известно много алгоритмов кодирования информации, основанных на различных принципах. Например, методы Шеннона-Фано, Хаффмана, Лемпела-Зива, арифметическое кодирование, Гилберта-Мура, «Стопка книг» и другие. Из них метод Хаффмана оптимален в отношении минимизации средней длины кодового слова. В настоящей статье разработан новый метод кодирования и упаковки информации на основе неравенства Крафта. Этот метод имеет ряд преимуществ по сравнению с методом Хаффмана:

− алгоритм достаточно прост и нагляден, не требует сложных математических расчётов;

− кодирование информации этим методом не является однозначным, а имеет много вариантов кода, что позволяет обеспечить дополнительную защиту информации.

Тестирование показало, что при условии выполнения неравенства Крафта для всех длин кодовых слов, минимальная средняя длина кодового слова по разработанному алгоритму такая же, как и по методу Хаффмана, а значит разработанный метод можно считать оптимальным.

Описание метода кодирования на основе неравенства Крафта

В теории кодирования, неравенство Крафта даёт необходимое и достаточное условие существования разделимых и префиксных кодов, обладающих заданным набором длин кодовых слов.

Теорема Крафта: Если целые числа удовлетворяют неравенству:

(1)

то существует код, обладающий свойством префикса с алфавитом объема , длины кодовых слов в котором равны этим числам. Обратно, длины кодовых слов любого кода, обладающего свойством префикса, удовлетворяют указанному неравенству.

Пусть заданы кодируемый и кодирующий алфавиты, состоящие из n и d символов, соответственно, и заданы желаемые длины кодовых слов , тогда необходимым и достаточным условием существования разделимого и префиксного кодов, обладающих заданным набором кодовых слов, является выполнение неравенства (1).

Разработка алгоритма кодирования на основе неравенства Крафта

Входными данными для программы являются текстовые данные, введенные с клавиатуры, либо текстовый файл формата SLN, загруженный с компьютера.

1. Необходимо посчитать и запомнить частоту (вероятности появления) 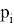каждого символа в сообщении по формуле

=

(2)

где — количество вхождений -го символа в сообщение, а — количество символов в сообщении.

2. По посчитанным вероятностям 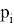считаем теоретические длины кодовых слов по формуле

(3),

округляя их до целых чисел.

3. Проверяем длины кодовых слов 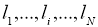на соответствие неравенству Крафта:

≤ 1

(4)

4. Если длины кодовых слов удовлетворяют неравенству Крафта, то переходим к следующему шагу. Иначе, необходимо вывести сообщение о том, что не существует префиксного кода с заданными длинами кодовых слов.
5. Начиная с первого символа в сообщении 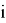= 1 проверяем его на соответствие условию: 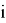≤ 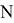? Пока данное условие выполняется, переходим к следующему шагу. Если не выполняется, то это значит, что мы прошли по всем символам алфавита, и новых символов в алфавите нет, после чего выходим из алгоритма и выводим закодированное сообщение.
6. Условимся, что все правые ветви всегда — единицы, левые ветви — нули (дерево хранится в памяти в виде матрицы или двумерной таблицы точек c двумя координатами, где 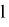- уровень дерева, k — порядковый номер точки на уровне.) Отмечаем концевую точку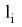на соответствующем уровне бинарного дерева, запоминая при этом координаты точки ( 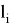— уровень дерева, k — порядковый номер точки на уровне), выбирая при этом любой свободный узел на уровне.
7. Проверяем, не является ли уровень дерева 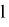- нулевым (корнем дерева): 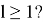Если данное условие не выполняется, то это означает, что мы находимся на нулевом уровне (в корне дерева). Возвращаемся к шагу 5. Если данное условие истинно, то переходим к следующему пункту алгоритма.
8. Проходим от концевой точки (листа) к корню дерева, запоминая путь (все узлы от листа до корня) по следующему алгоритму:
9. Находим остаток от деления порядкового номера концевой точки на 2 используя следующую операцию k mod 2. Если в остатке 1, то записываем в начало кодового слова 0, если в остатке 0, то записываем 1. После каждого действия возвращаемся к шагу 6.

Блок-схема алгоритма кодирования представлена на рисунке 1.

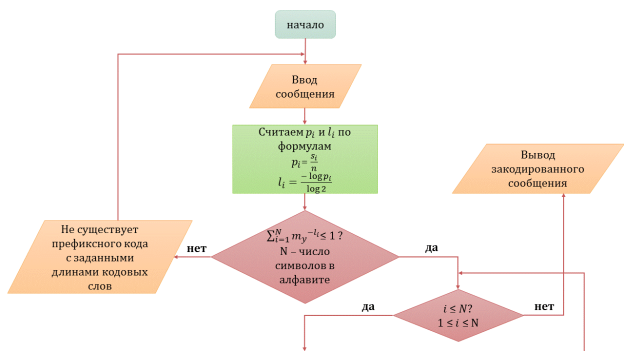
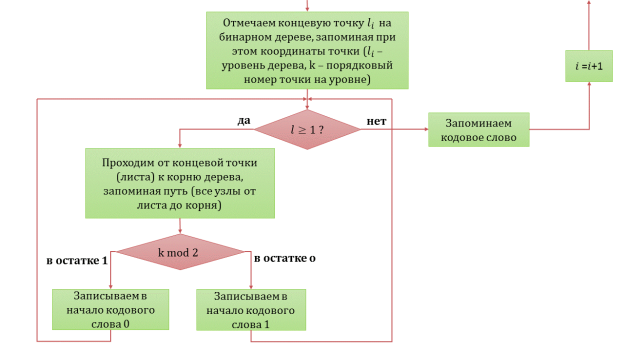
Рис. 1. Блок-схема алгоритма кодирования на основе неравенства Крафта

Разработка алгоритма декодирования на основе неравенства Крафта

На вход программы декодирования подается код (последовательность кодовых слов) полученный при кодировании полученного на ход сообщения.

1. Осуществляем проверку, не пуст ли массив данных? Если не пуст, то переходим к следующему шагу. Если пуст, то сравниваем найденные кодовые слова с запомненными, находим соответствующие символы и выводим дешифрованное сообщение.
2. Проходим по введенной последовательности 0 и 1 по ветвям имеющегося дерева от его корня к листьям (концевым точкам) на каждом шаге сравнивая координаты узла с известными координатами концевых точек. Проверяем, совпадают ли координаты узла с координатами одной из концевых точек (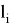, k)? Если нет, то повторяем этот шаг снова. Если да, то запоминаем найденное кодовое слово и возвращаемся к шагу 2.

Блок-схема алгоритма декодирования представлена на рисунке 2.

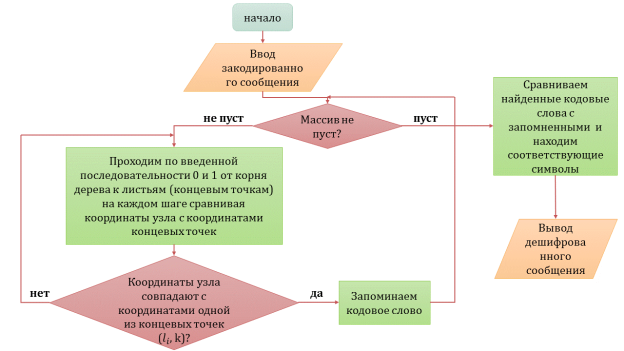
Рис. 2. Блок-схема алгоритма декодирования на основе неравенства Крафта

Разработка алгоритма эффективной упаковки

В предыдущем абзаце нами уже было закодировано сообщение «колобок полотенце уволок» и построено кодовое дерево. Но в сравнении с методом Хаффмана средняя длина кодового слова больше, чем у Хаффмана. Некоторые кодовые слова по разработанному методу получаются длиннее, чем у Хаффмана.

Суть алгоритма уплотнения в том, чтобы сократить по нашему методу и соответственно увеличить эффективность кодирования. Это возможно за счёт наличия «свободных» точек на кодовом дереве, в которые можно перенести кодовые слова с более высоких уровней, тем самым избавляясь от избыточности и сокращая длину некоторых кодовых слов.

Опишем алгоритм эффективной упаковки.

Проходим от корня дерева по всем уровням и ищем «свободные» точки.

Свободными точками для всех уровней дерева кроме предпоследнего будем считать узлы, которые не являются кодовым словом (концевой точкой), и из которых не выходит ни одно кодовое слово. Для предпоследнего уровня «свободной» точкой считается та, которая не является концевой и из которой не выходит 2 кодовых слова, то есть либо ноль, либо одно.

1. Итак, начиная с первого уровня первым делом проверяем, не является ли этот уровень последним? Если он последний, то алгоритм упаковки не имеет смысла и закодированное сообщение остаётся неизменным. Если уровень не является последним, то переходим к следующему шагу.
2. На каждом уровне осуществляем проход по всем точкам по порядку, 1≤ 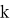≤ 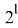и проверяем, не является ли данная точка кодовым словом (концевой), так как это необходимое условие для «свободной» точки.
3. Если на предыдущем шаге проверяемая точка оказалась «концевой», то переходим к шагу 4, а если нет, то переходим к шагу 5.
4. Проверяем, не является ли данная точка последней на уровне. Если является, то переходим на следующий уровень и повторяем шаги 1–4, если не является, то переходим на следующую по порядку точку и повторяем шаги 2–4.
5. Поскольку понятия «свободной» точки на предпоследнем уровне дерева и на всех остальных отличаются, то необходимо проверить условие, не является ли уровень, на котором мы находимся предпоследним. Если не является, то переходим к шагу 6. Если уровень является предпоследним, то переходим к шагу 7.
6. Проверяем условие, проходят ли через текущую точку одно или более кодовых слова. Если да, то повторяем шаги начиная с 4. Если нет, то переходим к шагу 8.
7. Если на 5 шаге выяснилось, что уровень, на котором находимся, является предпоследним, то проверяем условие, проходят ли через эту точку 2 кодовых слова, так как если уровень предпоследний, то выйти из точки могут максимум 2 кодовых слова. Если через точку проходят 2 кодовых слова, то свободной точка не считается и повторяем шаги начиная с 4. Если через текущую точку на предпоследнем уровне проходит одно кодовое слово, либо не проходят вовсе, то переходим к шагу 8.
8. Текущая точка является свободной, мы запоминаем ее координаты и начинаем поиск «концевых» точек на вышележащих уровнях.
9. На этом шаге проверяем, нашлись ли на вышележащем уровне концевые точки. Если да, то переносим в «свободную» точку найденную «концевую» точку с наибольшей вероятностью 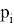на своём уровне и повторяем шаги 2–9. Если концевых точек нет на вышележащем уровне, то переходим к следующему шагу.
10. переходим на следующий 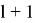уровень и повторяем шаги 10–11.
11. Проходим по алгоритму до тех пор, пока дерево не будет полностью упакованным. Дерево считается плотно упакованным, если на нём не осталось свободных точек.
12. Блок-схема алгоритма эффективной упаковки представлена на рисунке 3.

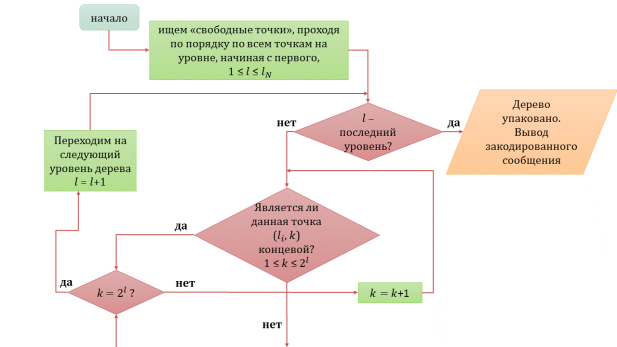
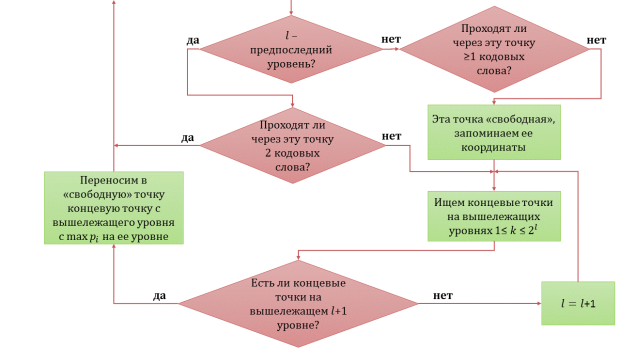
Рис. 3. Блок-схема алгоритма эффективной упаковки

Рассмотрим наглядно алгоритм эффективной упаковки на кодовом дереве [рис.4].

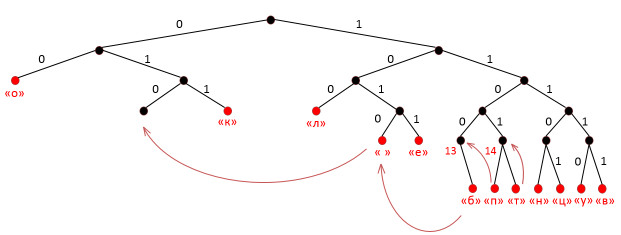
Рис. 4. Алгоритм эффективной упаковки

Итак, после применения алгоритма эффективной упаковки длины кодовых слов сокращаются, и средняя длина кодового слова становится такой же, что и у Хаффмана, а значит, разработанный алгоритм оптимален.

Выводы

Разработанный алгоритм и алгоритм Хаффмана были протестированы на девяти различных вариантах входных данных и во всех случаях показали одинаковый результат. Сравнение проводилось по средней длине кодового слова. Критерий оценки — минимальная средняя длина кодового слова при условии, что кодовые слова удовлетворяют неравенству Крафта.

Таким образом, результаты экспериментальных исследований подтвердили, что разработанный алгоритм кодирования является оптимальным. А значит, его можно успешно применять на практике в архиваторах, основанных на статистических методах кодирования.

Литература:

1. Ватолин, Д. В. Методы сжатия данных. — М.: «Диалог-МИФИ», 2002.
2. Ломакин, Д.В., Ломакина, Л.С., Пожидаев, А. С. Вероятность. Информация. Классификация: учеб. пособие / НГТУ им. Р. Е. Алексеева. — Н. Новгород, 2014. — 128.
3. Могилевсая, Н. С. Методы сжатия информации. Алгоритмы Хаффмана и Лемпеля — Зива. Методические указания по курсу «Теория информации». / Ростов -на –Дону: издательский центр ДГТУ, 2011, 14с.
4. Яглом, А.М., Яглом, И. М. Вероятность и информация. — М.: Наука, 1973.- 511 с.
5. Bell, T.C., Cleary, J.G., Witten, I.H.: Text Compression. Prentice Hall, Englewood Cliffs, NJ (1990)Google Scholar.
6. Huffman, D. A.: A Method for the Construction of Minimum-Redundancy Codes. Proc. IRE, Vol.40 (1952) 1098–1101CrossRefGoogle Scholar.
7. Long, D., Jia, W.: The Optimal Encoding Schemes. Proc. of 16th World Computer Congress, 2000, Bejing, International Academic Publishers (2000) 25–28.