Закономерности изменчивости и распределения антропометрических признаков
Авторы: Абдурахманова Фируза Абдуфармановна, Узакова Лайло Палвановна, Турсункулова Махсуда Суяркуловна
Рубрика: Легкая промышленность
Опубликовано в Техника. Технологии. Инженерия №2 (12) апрель 2019 г.
Дата публикации: 04.04.2019
Статья просмотрена: 679 раз
Библиографическое описание:
Абдурахманова, Ф. А. Закономерности изменчивости и распределения антропометрических признаков / Ф. А. Абдурахманова, Л. П. Узакова, М. С. Турсункулова. — Текст : непосредственный // Техника. Технологии. Инженерия. — 2019. — № 2 (12). — С. 27-30. — URL: https://moluch.ru/th/8/archive/120/4064/ (дата обращения: 20.04.2024).
В данной статье приведены установление размерной типологией пределы изменчивости (вариабельности) признаков внутри и среди различных групп населения, соотношение размеров стоп, выбор размерных признаков, необходимых для проектирования обуви, связь между антропометрическими признаками при разработка программы и методики измерений, пример составления вариационного ряда.
В условиях современного массового производства изделий из кожи, когда обувь и перчатки изготовляют для «неизвестного» потребителя, исключается возможность непосредственного обмера стоп и кистей каждого индивидуума. В то же время промышленность обязана максимально обеспечить население страны удобными изделиями. Этого можно достичь только в том случае, если все разнообразие стоп (кистей) будет представлено оптимальным для промышленности и населения числом типов. Тогда изделия, изготовленные по размерным признакам выбранных типов, будут удовлетворять большинство людей нашей страны. Система таких типов и кистей называется размерной типологией. Необходимо также знать, какое количество людей, относящихся к каждому из выделенных типов, проживает на территории нашей страны. Кроме того, для создания удобных изделий надо найти правильное соотношение размеров и формы стопы (кисти) с размерами и формой как обуви (перчаток) в целом, так и ее деталей. А для этого следует установить связь между антропометрическими признаками.
Для решения указанных задач нужно получить детальную характеристику морфологических типов, встречающихся среди населения, т. е. определить величины антропометрических признаков, характеризующих морфологические типы, пределы изменчивости (вариабельности) признаков внутри и среди различных групп населения, соотношение размеров стоп или кистей. Как отмечалось выше, указанные данные получают при антропологических исследованиях по соответствующей программе.
Проведению исследований стоп (кистей) должны предшествовать выбор размерных признаков, необходимых для проектирования обуви (перчаток и рукавиц), разработка программы и методики измерений, установление числа лиц, подлежащих измерению, их возрастного, профессионального и национального состава, места (пункта) измерений [1].
По намеченной программе измеряют группу людей, которые могут служить представителями изучаемого населения. Группа людей может представлять все население в том случае, если различные значения размерных признаков у всего населения будут встречаться с такой же частотой, как у выбранной группы людей.
Все население, проживающее в нашей стране, назовем генеральной совокупностью. Обмерить стопы (кисти) всего населения нашей страны, т. е. всей генеральной совокупности, невозможно и нет необходимости. Однако нужно обмерить стопы (кисти) такого числа людей, которое в достаточной степени могло бы характеризовать стопы (кисти) населения всей страны. Группу людей, стопы (или кисти) которых измеряют, называют выборкой [1].
Выборкой из генеральной совокупности называют часть генеральной совокупности, отобранной с соблюдением требований, определяемых целью исследований, и исследуемой для того, чтобы характеризовать всю генеральную совокупность. Выборка будет называться представительной (репрезентативной) для всей генеральной совокупности, если она достаточно хорошо представляет пропорции генеральной совокупности (например, если число выделенных типов стоп будет встречаться в ней с той же частотой, что и у всего населения). При составлении выборки должно соблюдаться основное требование — она должна быть случайной (стохастической), т. е. каждый человек должен иметь равные шансы быть обмеренным. Кроме того, при обмере взрослого населения в выборку должны быть включены взрослые люди всех возрастных групп: младшей (18–29 лет), средней (30–44 года), старшей (свыше 45 лет) с учетом распределения по годам в каждой возрастной группе.
Исследование должно проводиться как среди городского, так и среди сельского населения. В выборку включают людей различных профессий, так как наблюдаются значимые отклонения размеров стоп, а особенно размеров кистей у людей разных профессий.
Численность каждой из перечисленных категорий должна входить в выборку в тех же пропорциях, с теми же относительными частотами, что и в генеральной совокупности.
Затем намечаются населенные пункты, где предполагается производить измерения.
При обмере стоп (кистей) детей в зависимости от целей исследований в выборку включают детей одного годового периода (например, для нахождения прироста длины стопы за год) или детей всех возрастных групп, т. е. каждого года жизни от 1 года до 18 лет (например, при разработке размерной типологии стоп детей) [2].
Выборка может быть типологической, т. е. объекты исследования отбирают сознательно, учитывая их типичность и принадлежность к данному типу. Например, составляют случайную выборку для установления средних значений длины и обхвата стоп в пучках, а для изучения связей между размерными признаками — типологическую выборку, в которую включают только людей, имеющих длину и обхват стоп в пучках, равные среднетипичным значениям этих размерных признаков.
Объем (численность) выборки зависит от конечной цели работы. Считают, что при обмере стоп и кистей результаты исследований можно считать достоверными (полученные результаты характеризуют всю генеральную совокупность), если численность выборки составляет не менее 500 человек. Объем типологической выборки меньше, чем объем стохастической.
При обследовании детей каждого годового периода измеряют по 100–150 стоп (кистей) детей каждого пола.
Данные обмера обрабатывают методами математической статистики. Для каждого из размерных признаков определяют такие статистические параметры, которые характеризуют величину и вариабельность признака в выборке, а следовательно, и в генеральной совокупности. Как бы ни была однородна изучаемая группа людей, значения любого из антропометрических признаков обнаруживают изменчивость, т. е. различные значения любого из антропометрических признаков встречаются с разной частотой — одни чаще, другие реже. Для характеристики вариабельности антропометрических признаков, прежде всего при обработке данных обмера, составляют так называемый вариационный ряд. Он представляет собой двойной ряд чисел, состоящий из значений признака, сгруппированных. В классы, и соответствующих каждому классу частот (вариантов). Частотой вариантов называют число вариантов, попадающих в тот или иной класс. Вариационный ряд можно изобразить графически в виде вариационной кривой, или кривой распределения.
Рассмотрим пример составления вариационного ряда и построения кривой распределения на конкретном материале. Допустим, что нужно проанализировать данные, полученные при измерении длины стоп 124 детей. Сначала эти данные представляют в виде упорядоченной таблицы, где все полученные длины стоп располагают в порядке возрастания. Затем устанавливают наименьшие (min) и наибольшие (max) значения длины стопы в данной выборке: min=144,2 мм, max=172 мм [3].
Чтобы было удобно выполнять дальнейшие вычисления, значения признака группируют в классы. Число классов должно быть порядка 10–15, так как меньшее число классов снижает точность расчета. Если число наблюдений в выборке менее 30, значения признака в классы не группируют.
Таблица 1
Длина, мм, стоп детей
|
№ т/р |
Д, мм |
№ п/п |
Д, мм |
№ п/п |
Д, мм |
№ п/п |
Д, мм |
№ п/п |
Д, мм |
|
1 |
144,2 |
26 |
153,9 |
51 |
157,1 |
76 |
159,3 |
101 |
162,2 |
|
2 |
145,5 |
27 |
154,1 |
52 |
157,3 |
77 |
159,3 |
102 |
162,4 |
|
3 |
147,2 |
28 |
154,2 |
53 |
157,4 |
78 |
159,4 |
103 |
162,7 |
|
4 |
147,6 |
29 |
154,6 |
54 |
157,6 |
79 |
159,4 |
104 |
162,7 |
|
5 |
147,9 |
30 |
154,8 |
55 |
157,6 |
80 |
159,8 |
105 |
163,1 |
|
6 |
148,5 |
31 |
154,9 |
56 |
157,7 |
81 |
159,9 |
106 |
163,3 |
|
7 |
149,2 |
32 |
155,2 |
57 |
157,8 |
82 |
160,0 |
107 |
163,4 |
|
8 |
149,4 |
33 |
155,2 |
58 |
157,8 |
83 |
160,1 |
108 |
163,5 |
|
9 |
150,3 |
34 |
155,3 |
59 |
157,9 |
84 |
160,2 |
109 |
163,6 |
|
10 |
150,9 |
35 |
155,4 |
60 |
158,0 |
85 |
160,4 |
110 |
163,8 |
|
11 |
151,2 |
36 |
155,5 |
61 |
158,2 |
86 |
160,4 |
111 |
163,9 |
|
12 |
151,3 |
37 |
155,7 |
62 |
158,2 |
87 |
160,6 |
112 |
164,0 |
|
13 |
151,4 |
38 |
155,7 |
63 |
158,3 |
88 |
160,7 |
113 |
164,7 |
|
14 |
151,6 |
39 |
155,8 |
64 |
158,3 |
89 |
160,7 |
114 |
165,2 |
|
15 |
151,9 |
40 |
155,9 |
65 |
158,4 |
90 |
160,8 |
115 |
165,4 |
|
16 |
152,3 |
41 |
155,9 |
66 |
158,5 |
91 |
160,9 |
116 |
165,5 |
|
17 |
152,4 |
42 |
156,0 |
67 |
158,5 |
92 |
161,2 |
117 |
165,7 |
|
18 |
152,8 |
43 |
156,0 |
68 |
158,6 |
93 |
161,2 |
118 |
166,0 |
|
19 |
153,1 |
44 |
156,3 |
69 |
158,7 |
94 |
161,3 |
119 |
166,2 |
|
20 |
153,2 |
45 |
156,4 |
70 |
158,8 |
95 |
161,4 |
120 |
167,1 |
|
21 |
153,2 |
46 |
156,4 |
71 |
159,0 |
96 |
161,5 |
121 |
168,4 |
|
22 |
153,4 |
47 |
156,6 |
72 |
159,0 |
97 |
161,6 |
122 |
169,1 |
|
23 |
153,4 |
48 |
156,7 |
73 |
159,1 |
98 |
161,8 |
123 |
171,1 |
|
24 |
153,6 |
49 |
156,8 |
74 |
159,2 |
99 |
161,8 |
124 |
172,0 |
|
25 |
153,8 |
50 |
156,9 |
75 |
159,2 |
100 |
162,0 |
Значения, объединенные в один класс, отделены чертой.
Классовый интервал — интервал между двумя смежными классами.
dх =(max- min)/k,
где k=10 или 15.
Разность max- min называют размахом вариабельности признака в выборке. Если при расчете классового интервала получают дробную величину, ее округляют до целого числа или до 0,5.
Таблица 2
Вариационный ряд по длине стоп детей
|
Границы классовых интервалов, мм |
Частота вариантов в каждом классе |
Границы классовых интервалов, мм |
Частота вариантов в каждом классе |
|
143,5–145,4 |
1 |
159,5–161,4 |
16 |
|
145,5–147,4 |
2 |
161,5–163,4 |
12 |
|
147,5–149,4 |
5 |
163,5–165,4 |
8 |
|
149,5–151,4 |
5 |
165,5–167,4 |
5 |
|
151,5–153,4 |
10 |
167,5–169,4 |
2 |
|
153,5–155,4 |
12 |
169,5–171,4 |
1 |
|
155,5–157,4 |
18 |
171,5–173,4 |
1 |
|
157,5–159,4 |
26 |
N =124 |
Таблица 3
Вариационный ряд по длине стопы детей для построения кривой распределения
|
Граница классовых интервалов, мм |
Среднее значение класса, мм |
Частота вариантов в каждом классе |
|
143,5–147,4 |
145,5 |
3 |
|
147,5–151,4 |
149,5 |
10 |
|
151,5–155,4 |
153,5 |
22 |
|
155,5–159,4 |
157,5 |
44 |
|
159,5–163,4 |
161,5 |
28 |
|
163,5–167,4 |
165,5 |
13 |
|
167,5–171,4 |
169,5 |
3 |
|
171,5–175,4 |
173,5 |
1 |
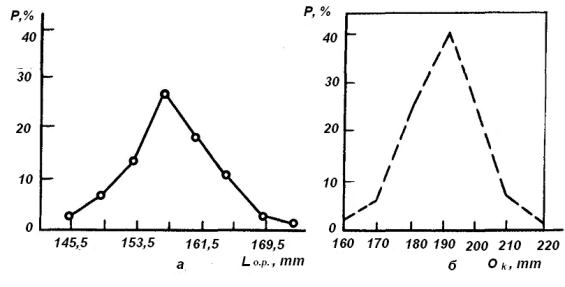
Рис. 1. Вариационные кривые по длине стопы детей (а) и обхвату кисти руки женщин (б)
Для каждого вариационного ряда
![]() ,
,
где Pxi- повторение каждого вариационного ряда.
Среднеарифметическое величина показателей определяется следующим образом.
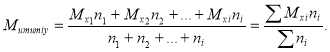
Литература:
- Т. С. Кочеткова, В. М. Ключникова «Антропологические и биомеханические основы конструирования изделий из кожи».М., 1991.
- Кранс В. М., Колесникова Н. А., Луковенко Г. В. Морфологические особенности развития детской стопы. Москва., ЦИТО. 1980.
- Кранс В. М., Колесникова Н. А., Луковенко Г. В. О размерной типологии стоп школьников. Москва., ЦИТО. 1980.
Похожие статьи
Вариационный ряд антропометрических признаков студенток...
Объединение значений признака в классы для построения вариационной кривой проводится по
На оси ординат у откладывают частоту встречаемости признака.
Подобная закономерность в вариабельности значений признака в вариационном ряду наблюдается у...
Мода и медиана вариационного ряда антропометрических...
число значений, вариационный ряд, класс, бухара, обхват груди, число классов, классовый интервал, построение кривой
В разработанной размерной типологии населения стран СНГ в качестве ведущих признаков для выбора типовых фигур у женщин приняты длина тела...
Сплошное и выборочное наблюдение: теоретический аспект
Вариационный ряд антропометрических признаков студенток... Математическая статистика — наука, которая изучает вопросы соотношения генеральной совокупности и
В том случае, если в выборке число наблюдений менее 60, значения признака не группируют в классы.
Статистическая обработка результатов гидравлического...
Если в генеральной совокупности единицы располагаются случайным образом по отношению к изучаемому признаку, то механический
Дисперсию малой выборки s следует вычислять по формуле, включающей поправку Бесселя.
Равенство генеральных дисперсий в этих группах.
Статистические методы при управление качеством продукции на...
число значений, вариационный ряд, класс, бухара, обхват груди, число классов, классовый интервал, построение кривой распределения, обхват талии
Для измерения колебания признака используют вариационный размах, дисперсию и среднее квадратическое отклонение.
Проверка статистических гипотез в психолого-педагогических...
– качественные данные — данные представляющие собой частоту встречаемости какого-либо свойства в исследуемой группе. (число людей
Задачей анализа полученных данных является изучение частоты встречаемости тех или иных значения признака в эксперименте.
Анализ процедур генерации ключей криптографических алгоритмов.
Вариационный ряд антропометрических признаков студенток... Определив число классов для заданной численности выборки
Вправо и влево от класса с максимальной численностью на кривой распределения (или вверх и вниз от этого класса в табл. 4) число значений признака в...
Вычисление статистических показателей с использованием...
В результате можно получить следующие варианты распределения: 1 вариант.
Для анализа распределения необходимы числовые значения статистических показателей, позволяющие оценить колебания значений изучаемого признака и взаимосвязь его с другими признаками
Методы математической статистики в технических исследованиях
Для измерения колебания признака используют вариационный размах, дисперсию и
Вариационный размах R есть разность между экстремальными значениями частотного ряда: R
Дисперсия – средняя арифметическая из квадратов отклонений вариантов от их средней...
Похожие статьи
Вариационный ряд антропометрических признаков студенток...
Объединение значений признака в классы для построения вариационной кривой проводится по
На оси ординат у откладывают частоту встречаемости признака.
Подобная закономерность в вариабельности значений признака в вариационном ряду наблюдается у...
Мода и медиана вариационного ряда антропометрических...
число значений, вариационный ряд, класс, бухара, обхват груди, число классов, классовый интервал, построение кривой
В разработанной размерной типологии населения стран СНГ в качестве ведущих признаков для выбора типовых фигур у женщин приняты длина тела...
Сплошное и выборочное наблюдение: теоретический аспект
Вариационный ряд антропометрических признаков студенток... Математическая статистика — наука, которая изучает вопросы соотношения генеральной совокупности и
В том случае, если в выборке число наблюдений менее 60, значения признака не группируют в классы.
Статистическая обработка результатов гидравлического...
Если в генеральной совокупности единицы располагаются случайным образом по отношению к изучаемому признаку, то механический
Дисперсию малой выборки s следует вычислять по формуле, включающей поправку Бесселя.
Равенство генеральных дисперсий в этих группах.
Статистические методы при управление качеством продукции на...
число значений, вариационный ряд, класс, бухара, обхват груди, число классов, классовый интервал, построение кривой распределения, обхват талии
Для измерения колебания признака используют вариационный размах, дисперсию и среднее квадратическое отклонение.
Проверка статистических гипотез в психолого-педагогических...
– качественные данные — данные представляющие собой частоту встречаемости какого-либо свойства в исследуемой группе. (число людей
Задачей анализа полученных данных является изучение частоты встречаемости тех или иных значения признака в эксперименте.
Анализ процедур генерации ключей криптографических алгоритмов.
Вариационный ряд антропометрических признаков студенток... Определив число классов для заданной численности выборки
Вправо и влево от класса с максимальной численностью на кривой распределения (или вверх и вниз от этого класса в табл. 4) число значений признака в...
Вычисление статистических показателей с использованием...
В результате можно получить следующие варианты распределения: 1 вариант.
Для анализа распределения необходимы числовые значения статистических показателей, позволяющие оценить колебания значений изучаемого признака и взаимосвязь его с другими признаками
Методы математической статистики в технических исследованиях
Для измерения колебания признака используют вариационный размах, дисперсию и
Вариационный размах R есть разность между экстремальными значениями частотного ряда: R
Дисперсия – средняя арифметическая из квадратов отклонений вариантов от их средней...







