Методическая разработка урока информатики по теме «Неформальный подход к формальным исполнителям»: образовательный модуль, направленный на отработку задания 6 КЕГЭ 2023 года



Методическая разработка составлена на основе и в соответствии с требованиями к результатам освоения основной образовательной программы среднего общего образования, определенным Федеральным компонентом государственного образовательного стандарта среднего (полного) общего образования (ФГОС СОО) и проверяемым заданиями экзаменационной работы КЕГЭ. Содержание урока соответствует «Перечню проверяемых требований к результатам освоения основной образовательной программы среднего общего образования по информатике» и «Перечню элементов содержания, проверяемых на едином государственном экзамене по информатике», перечисленных в Кодификаторе ЕГЭ 2023 г., подготовленных федеральным государственным бюджетным научным учреждением «Федеральный институт педагогических измерений».

Цель урока : формирование функциональной грамотности у обучающихся старшей школы посредством решения учебно-практических задач различными методами в рамках подготовки к ЕГЭ.

Деятельностная цель : формирование у учащихся способностей к структурированию и систематизации изучаемого предметного содержания с использованием знаний, полученных в том числе в других предметных областях, а также метапредметных умений и навыков.

Содержательная цель: закрепление новых и коррекция изученных ранее способов решения задач на определение возможных результатов работы простейших алгоритмов управления исполнителями и вычислительных алгоритмов.

Задачи урока :

1. Изучить основные типы задач, которые могут быть предложены в реальных вариантах экзаменационной работы при подготовке к решению Задания 6 ЕГЭ по информатике в 2023 году.
2. Систематизировать приемы решения типовых задач Задания 6.
3. Выработать стратегию оптимального решения конкретной задачи
4. Научиться определять результат работы простейших алгоритмов управления исполнителями и вычислительных алгоритмов

Планируемые образовательные результаты:

Предметные:

формирование умения не только исполнять алгоритм, написанный для исполнителя с заданной системой команд, но и анализировать предлагаемые в задании последовательности команд для выбора оптимального способа решения конкретной задачи.

Метапредметные:

– познавательные : умение строить логические цепочки рассуждений, встраивая в них межпредметные связи; проверять полученный результат на практике, используя все доступные методы и средства;

– регулятивные : планирование своих действий; умение критически анализировать полученный результат;

– коммуникативные : умение формулировать собственные мысли; задавать вопросы; высказывать и обосновывать свою точку зрения умение слушать собеседника и вести диалог с людьми в процессе учебной, а затем и в профессиональной деятельности.

Личностные:

– развитие творческих способностей учащихся, логического мышления;

– умение планировать свою деятельность; формирование навыков самостоятельного принятия решений, самоорганизации и самоконтроля;

– формирование функциональной грамотности и алгоритмического мышления, необходимых для дальнейшей профессиональной деятельности в современном обществе.

Формы обучения: фронтальная, групповая, парная, индивидуальная.

Методы обучения : кейс-метод (метод конкретных ситуаций).

Технологии обучения : технологии развития читательской, математической и естественнонаучной грамотности, критического мышления, информационно-коммуникационные технологии, здоровьесберегающая технология.

Основные термины и понятия урока : Исполнитель, СКИ, координатная плоскость, пропорции, правильные фигуры, внутренний и внешний углы, параллельный перенос, тангенс угла, период, технология работы с фигурами в текстовом редакторе, технология работы с данными в электронных таблицах, работа с библиотеками в Python, смена форм деятельности.

Оборудование и программное обеспечение : магнитно-маркерная доска, демонстрационный комплект (ПК учителя и проектор), ноутбуки учеников, рабочие тетради, линейки, транспортир, текстовый процессор, среда программирования PyCharm.

Особенности организации учебного процесса : урок проходит в форме интерактивного образовательного модуля (2 учебных блока по 40 минут с перерывом между блоками 10 минут).

Условные обозначения :

– читательская грамотность — ЧГ,

– математическая грамотность — МГ,

– естественнонаучная грамотность — ЕГ,

– критическое мышление — КМ,

– информационно-коммуникационные технологии — ИКТ,

– ЗТ — здоровьесберегающие технологии.

Виды формируемой функциональной грамотности :

– ЧМ — смысловое чтение, быстрочтение.

– МГ — анализ числовых данных, градусная мера углов, координаты, геометрические фигуры на координатной плоскости, внешние и внутренние углы, наклоны и параллельный перенос, целые и натуральные числа, свойства треугольников, подобие, тангенса угла.

– ЕГ — анализ среды, в которой необходимо действовать при решении задачи, отработка понятий «право», «лево», поворот относительно направления головы объекта, движение вперед и назад по заданной траектории.

– КМ — анализ фигур, получаемых в результате выполнения Черепахой заданного алгоритма и выдвижение гипотез сценариев развития ситуаций, предложенных в алгоритмах Задания 6; упрощение предложенных в задачах Задания 6 алгоритмов без нарушения логики решения самих задач; применение алгебраических, геометрических и определённых самостоятельно зависимостей для облегчения подсчёта большого количества точек; использование чертежей, созданных при решении предыдущих задач, для решения следующей задачи; применение предметных и метапредметных знаний, полученных на уроке, в дальнейшей учёбе и при решении жизненных ситуаций.

– ИКТ — актуализация знаний по теме «Программирование», полученных на предыдущих этапах обучения, в том числе требования к синтаксису написания команд для Черепахи; умение выполнять вручную алгоритмы, предложенные в задачах; совершенствование навыков работы с таблицами и фигурами в текстовом процессоре; прикладное использование электронных таблицах; совершенствование навыков работы в Python.

– ЗТ — периодическое переключение взгляда учащихся смотреть «вдаль» — смотреть «вблизи», что позволяет снизить нагрузку на зрение.

Деятельность учителя .

Технология работы с кейсом (набором задач [1], предлагаемых для отработки выполнения Задания 6 КЕГЭ) позволяет применять на разных этапах урока следующие методы: нормативный (критериальный), который позволяет сделать предварительный анализ и выделить основные этапы решения задач; формализации, отбора и фокусирования; декомпозиции (разделения целого на части); классификаций для упорядочивания полученных учащимися знаний.

На уроке учитель:

 демонстрирует учащимся границы знаний и незнания, подводит учащихся к возможности систематизации типовых задач, предлагаемых в Задании 6;

 организует чередование видов деятельности (определили группу заданий, решили вместе образец, решили подобную задачу самостоятельно, сверили ответ);

 подводит учеников к акцентированию внимания на способах решения в зависимости от типа задачи и возможным трудностям, которые могут осложнить решение задачи или привести к неправильному ответу;

 побуждает учащихся к самостоятельным формулировкам оптимальных алгоритмов решения типовых задач.

 организует поисковую активность, направленную на выявление связей между новым материалом и ранее изученным;

 при самостоятельном решении учащимися задач оказывает консультирование;

 проводит экспресс-диагностику (организует опросы с получением быстрых ответов по пройденному на предыдущем этапе материалу, в случае необходимости просит сформулировать развернутый ответ);

 определяет выбор домашнего задания согласно желанию и уровню собственных способностей каждого учащегося;

 подводит итоги урока на примерах усвоенного предметного содержания.

Деятельность учеников :

– составляют конспект урока, при желании сопровождают записи схемами, которые рисует учитель на доске, и образцами решения задач каждого типа; помечают сложные места для дальнейшей отработки;

– анализируют предлагаемые учителем задачи, представляющие собой данные для исполнения алгоритмы, учатся самостоятельно интерпретировать прогнозируемые получаемые результаты;

– формулируют затруднения, встречающиеся при анализе алгоритмов;

– совместно с учителем формулируют вывод: задачи с углами 90, 60 и 120 решаются по одинаковым шаблонам, но из-за различий в формулировках вопросов могут решаться с применением разных алгоритмов;

– отрабатывают навыки решений типовых задач;

– для самопроверки решают задачи стандартизованным способом, для коррекции правильности рассуждений озвучивают свои результаты;

– опровергают распространённый в Интернете совет: на основании чертежа к задаче 5504 формулируют вывод, что угол 60 нельзя получить, соединяя точку (0,0) с точкой (4,7), такой чертеж приведет к ошибке и потере точек, удовлетворяющих ответу;

– формулируют оптимальный алгоритм решения задач, в которых Черепаха рисует равносторонний треугольник:

1) Если основание — четное число а, то количество точек с целочисленными координатами, лежащими внутри такого треугольника, будет рассчитываться с помощью электронных таблиц следующим образом: по формуле (а — 1): 2 считаем количество точек К для половины треугольника; затем увеличиваем К в 2 раза и прибавляем кол-во точек, лежащих на высоте.

2) Если основание — нечетное число а, то количество точек с целочисленными координатами, лежащими внутри такого треугольника, будет рассчитываться с помощью электронных таблиц следующим образом: по формуле (а — 1): 2 считаем количество точек К для половины треугольника; затем увеличиваем К в 2 раза.

Содержание учебного материала:

I учебный блок

Мотивация к учебной деятельности (2 минуты)

Вопросы для обсуждения:

1) Знаете ли вы, какие задания с Исполнителями встречаются в заданиях КЕГЭ?

2) С какими Исполнителями вы знакомы?

Для демонстрации задач используется [1], раздел Генератор, Задание 6.

Задание 6 относится к базовому уровню сложности, рекомендуемое время решения 4 минуты.

Актуализация знаний (5 минут)

На начальном этапе работы с Заданием 6 необходимо вспомнить СКИ Черепашки и результаты выполнения Черепахой простых алгоритмов.

Постановка цели (5 минут)

Фрагменты заданий с исполнителем Черепашка, предлагаемых учащимся для анализа, должны быть максимально разнообразны, например,

1) Повтори 9 [Вперёд 9 Направо 90]

2) Повтори 6 [Налево 120 Вперёд 6]

3) Направо 30 Повтори 30 [Направо 30 Вперёд 3 Направо 30]

4) Повтори 30 [Направо 30 Вперёд 3 Направо 30]

5) Вперёд 9 Направо 90Повтори 2 [Вперёд 3 Направо 90 Вперёд 3 Направо 270]

Повтори 2 [Вперёд 3 Направо 90] Вперёд 9

Усвоение новых знаний (15 минут)

Во всех рассматриваемых задачах, если не определено иначе, необходимо определить, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии не учитывать. При решении получаем правильные фигуры. Способ решения — без использования среды программирования.

I группа задач с углом поворота 90 

Фигура — квадраты и прямоугольники. Стандартная формула, применяемая при решении — количество точек равно (а — 1) х (b — 1), где а и b — количество шагов, пройденных Черепашкой.

Образец задачи ( 5505 ): Повтори 8 [Вперёд 12 Направо 90]

Образец решения задачи ( 5505 ): Черепаха рисует квадрат со стороной 12, значит, кол-во интересующих нас точек будет 11 x 11 = 121

II группа задач с углом 120 

Фигура — равносторонний треугольник. Вариант решения — построить треугольник с заданной стороной на сетке и посчитать точки вручную.

Образец задачи ( 5501 ): Повтори 12 [Вперёд 6 Направо 120]

Образец решения задачи ( 5501 ):

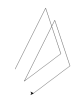
Черепаха рисует равносторонний треугольник со стороной 15, основание лежит на оси Y.

1) В текстовом процессоре Word создаем таблицу 10х10, в свойствах указываем значения строк, столбцов и ячеек 1 см — в этом случае при масштабировании листа с таблицей размер ячейки останется без изменений.

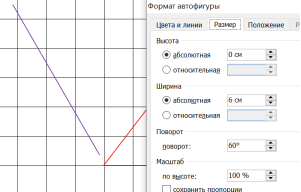
2) Добавляем на лист Фигуру равнобедренный треугольник, во вкладке Формат устанавливаем размер по ширине нужные нам 6 см.

3) Для получения точного месторасположения вершины добавляем на лист Отрезок длиной 6 см, поворачиваем его на 60 и параллельным переносом совмещаем нижний конец отрезка с вершиной в основании треугольника.

4) Совмещаем вершину, противоположную основанию, со вторым концом отрезка. Для более точного позиционирования можно использовать стрелки на клавиатуре.

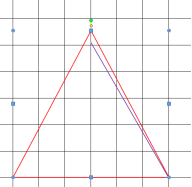
5) При необходимости увеличиваем масштаб чертежа, контролируя стрелками возможный сдвиг фигур, и считаем точки. Ответ: 13

Образец задачи для самостоятельного решения ( 5500 ):

Повтори 7 [Вперёд 10 Направо 120]

Образец решения задачи 1 для самостоятельного решения ( 5500 ):

Заметим, что можно посчитать точки у половины треугольника, умножить их количество на 2 и прибавить точки, лежащие на высоте. Получим 15 х 2 + 8 = 38 точек

III группа задач с углом поворота 60 

Фигура — правильный шестиугольник. Вариант решения — построить шестиугольник с заданной стороной на сетке и посчитать точки вручную.

Образец задачи 1 ( 5503 ):

Повтори 15 [Вперёд 4 Направо 60]

Определите, сколько точек с целочисленными положительными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

Образец решения задачи 1 ( 5503 ):

1) Заметим, что фигура, получаемая при помощи поворота на 60 — это правильный шестиугольник со стороной 4, построить в тетради его не каждый сможет, воспользуемся сеткой и треугольником, оставшимся от решения предыдущей задачи. Изменим размеры вспомогательного отрезка и основания треугольника на значение 4.

2) Используя команды Копировать и Отразить, составим нужную нам фигуру, проконтролируем расположение осей X и Y и посчитаем количество точек. (28 точек)

Этап коррекции (13 минут)

IV группа задач с углом поворота 120 

Фигура — равносторонний треугольник. Вариант решения — построить треугольник с заданной стороной на сетке и посчитать точки вручную.

Образец задачи ( 5504 ): Повтори 12 [Направо 60 Вперёд 6 Направо 60]

Образец решения задачи ( 5504 ):

1) В отличие от похожих задач, рассмотренной ранее, Черепаха начинает рисование равностороннего треугольника со стороной 6 с поворота , треугольник получается из-за сдвоенной команды поворота внутри цикла. Следовательно, и рисовать этот треугольник нужно по-другому. Разница в чертежах видна даже на скриншоте к предыдущей задаче.

2) Рисуем треугольник с нужной нам стороной 10 сразу в правильной ориентации на координатной плоскости, считаем точки и делаем вывод, что смещение основания с позиции целочисленных координат меняет итоговый ответ. Получили (17 х 2) + 8 = 42 точки.

V группа задач с углом поворота 120 

Фигура — равносторонний треугольник. Особенность — большое числовое значение для стороны треугольника, точки долго считать.

Образец задачи : Повтори 15 [Вперёд 25 Направо 120]

Образец решения задачи :

1) Заметим, что сетка 25х25 с размером 1 см х 1 см на стандартном листе А4 не поместится, необходимо в Параметрах страницы изменить формат бумаги на А3.

2) Строим равносторонний треугольник способом, разобранном на предыдущем этапе урока.

3) Рассмотрим половину построенного треугольника. Мы видим, что он представляет собой некоторое количество подобных вложенных треугольников с общей вершиной у основания треугольника. У самого маленького из них меньший катет равен 1, у следующего в два раза больше, т. е.2, и т. д. Причем точки с интересующими нас целочисленными координатами лежат на большем по размеру катете.

4) Рассмотрим первый треугольник с меньшим катетом, равным 1. Тангенс угла 60 равен примерно 1,73 (можно посчитать на калькуляторе или в Python). Так как тангенс угла есть отношение противолежащего катета к прилежащему, значит, больший катет тоже равен 1,73, причем на нем лежит ОДНА интересующая нас точка.

5) В нашем случае у всех следующих треугольников с меньшими катетами 2, 3 и т. д. интересующий нас угол также равен 60, значит, тангенсы этих углов также равны 1,73. Следовательно, увеличение размеров меньшего катета приводит к увеличению в такой же пропорции и большего катета (1 и 1,73; 2 и 2 х 1,73; 3 и 3 х 1,73 и т. д.). Построим эту зависимость в электронных таблицах.

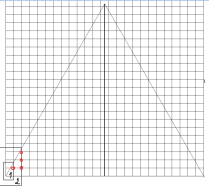
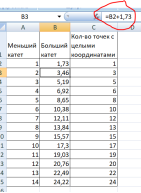
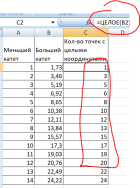
6) Анализируем наш чертеж. Для основания 25 нам нужно сначала суммировать точки левой половины. Максимальный катет у основания равен целое число (25: 2) = 12 . Выделим диапазон от 1 до 12 включительно и получим сумму 129 точек. Умножим это число на 2, чтобы учесть правую половину. Итого 258 точек.

Образец задачи для самостоятельного решения ( 5502 ): Повтори 15 [Вперёд 15 Направо 120]

Образец решения задачи ( 5502 ):

При помощи таблицы зависимости количества точек от размеров катетов для данной по условию стороны 15 определим количество точек, лежащих на катетах с меньшим размером от 1 до 7, то есть суммарно 45 точек. Далее 45 х 2 = 90. Ответ: 90

Перерыв 10 минут

II учебный блок

Этап закрепления (5 минут)

Блиц. Анализируем простейшие задачи из разобранных ранее типов:

1) Сколько точек внутри фигуры Повтори 15 [Вперёд 15 Направо 90]

2) Сколько точек внутри фигуры Повтори 15 [Вперёд 2 Направо 60]

3) Сколько точек внутри фигуры Повтори 15 [Вперёд 30 Направо 120]

Усвоение новых знаний (23 минуты)

Иногда в задаче сложно определить, какая фигура будет построена Черепашкой. В этой ситуации нам поможет среда программирования Python и библиотека turtle.

Так как в Python команды пишутся на английском языке, продублируем необходимые нам команды на этот язык. При этом вспомним, что команды можно писать сокращённо:

Циклы в Python реализуются стандартным образом. Главное — сверять фактическое расположение координатных осей с заданным в условии задачи. Обратим внимание, что необходимо будет увеличивать пропорционально количество шагов Черепашки, так как расстояния в 10 пикселей и им подобные позволят построить фигурку слишком маленького для дальнейшего анализа размера.

VI группа задач с неизвестной фигурой

Образец задачи ( 5591 ) :

Повтори 13 [Вперёд 10 Направо 90 Вперёд 10 Направо 90 Вперёд 30 Направо 90]

Сколько точек с целочисленными координатами находится внутри полученного контура? Точки, лежащие на полученной линии, не считать.

Образец решения задачи ( 5591 ) :

Составим программу в Python, запустим её и проанализируем полученный результат.

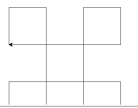
Очевидно, что для решения задачи нам даже нет необходимости менять размеры или сдвигать картинку выше. На рисунке видно, что у нас есть 5 квадратов со стороной 10, значит, количество интересующих нас точек равно 5 х (10–1) х (10–1) = 405

Образец задачи для самостоятельного решения ( 5554 ) :

Направо 30 Повтори 6 [Вперёд 7 Направо 120 Вперёд 7 Направо 60]

Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии не учитывать. Образец решения задачи ( 5554 ) :

Составим программу в Python, запустим её и проанализируем полученный результат. Получили ромб со стороной 7, малая диагональ лежит на оси X.

Первый поворот перед циклом в 30говорит о том, что ромб состоит из двух равносторонних треугольников. Как мы проходили ранее, количество точек будет равно 2 х (2 раза сумма точек в треугольниках со стороной 3) с добавлением точек на самой малой диагонали. (42 точки)

Образец задачи для самостоятельного решения ( 5775 ) :

Повтори 2 [Вперёд 10 Направо 90 Вперёд 20 Направо 90] Поднять хвост Назад 15 Направо 90 Назад 10 Налево 90 Опустить хвост Повтори 2 [Вперёд 30 Направо 90 Вперёд 40 Направо 90]

Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения.

Образец решения задачи ( 5775 ) :

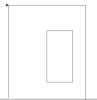
Составим программу в Python, запустим её и проанализируем полученный результат. Внутри пересечения фигур находится прямоугольник со сторонами 10 на 20, значит, внутри этого прямоугольника 9 х 19 точек и по контуру 2 х (10 + 20), итого 231 точка.

VII группа задач с неизвестной фигурой, исполнитель Чертежник

Чертежник рисует отрезки между точками с заданными координатами, добавим в СКИ Черепахи интуитивно понятную команду goto (x,y).

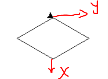
Образец задачи ( 5597 ) :

Повтори 20 раз

Сместиться на (10, 20) Сместиться на (5, -15) Сместиться на (-12, -9)

конец

Перед началом алгоритма Чертёжник находился в точке с координатами (0, 0). Определите, на каком расстоянии от начала координат окажется Чертёжник после выполнения алгоритма.

Образец решения задачи ( 5597 ) :

Без использования компьютера. Видим, что за 1 повтор общее смещение относительно точки (0,0) составит (3,-4), следовательно, за 20 повторов получим смещение (60,-80). Искомое расстояние считаем по теореме Пифагора. Получаем 100

С использованием компьютера . Составим программу в Python, запустим её и проанализируем полученный результат. Для удобства повторим цикл 2 раза.

Этап систематизации знаний (7 минут)

Вопросы, используемые для диагностики:

1. Основное отличие задач с алгоритмами для Черепахи от задач с алгоритмами для Чертежника.
2. В задачах какого типа не нужно использовать среду программирования.
3. Для чего мы подключаем к решению задачи Python.
4. Какие типовые ошибки можно допустить, решая задачи без использования среды программирования.
5. Какие типовые ошибки можно допустить, решая задачи с использованием Python.

Вопросы демонстрируются учителем на экране. Учащиеся отвечают устно, по желанию, так как элективный урок не имеет балльной оценочной системы. Во время ответов на вопросы учащиеся могут вносить дополнения к записям в тетради.

Каждый учащийся формулирует для себя ответ, первый, кто готов, отвечает вслух. Если у кого-то есть дополнения, учащиеся высказывают его по очереди, не перебивая беседу. Активное слушание позволяет избежать повторов при ответах.

Каждый правильный ответ оценивается вербально с поощрением ученика. На каждом точном и полном ответе учитель акцентирует внимание учащихся, тем самым повторяя правильно сформулированные высказывания по теме урока. Акцент также делается и на неполных ответах, чтобы у учеников была возможность уточнить некоторые выводы.

Если кто-то из учеников не отвечает на вопросы, учитель задает такому ученику наводящие вопросы.

Этап объяснения домашнего задания (2 минуты)

Учитель определяет выбор домашнего задания на основе задач [1], [2], [3] согласно желанию и уровню собственных способностей каждого учащегося.

Этап рефлексии (3 минуты)

По итогам кейса и приобретенного опыта обсуждаются вопросы:

Что было наиболее сложным? Что было наиболее простым? Самый сложный момент урока? Общее впечатление от Задания 6? Основной навык, который вы получили? Какой ошибки в будущем вы сможете избежать?

Демонстрационные материалы, созданные на основе [1].

Все скриншоты, используемые в методической разработке, авторские.

Литература:

1. Сайт К. Ю. Полякова (https://kpolyakov.spb.ru/school/ege.htm),
2. Образовательный портал для подготовки к экзаменам РешуЕГЭ Д.Гущина (https://inf-ege.sdamgia.ru/),

3. Информатика с Джобсом | ЕГЭ 2023 (https://vk.com/inform_web).

4. Сайт ФИПИ, url-адрес https://fipi.ru/
5. Приказ Министерства просвещения Российской Федерации от 12.08.2022 № 732 «О внесении изменений в федеральный государственный образовательный стандарт среднего общего образования, утвержденный приказом Министерства образования и науки Российской Федерации от 17 мая 2012 г. № 413".