Система кружковых занятий по решению японских головоломок для учащихся 5–6-х классов
Автор: Абашкин Алексей Николаевич
Рубрика: Внешкольное (дополнительное) образование и воспитание
Опубликовано в Образование и воспитание №3 (29) июнь 2020 г.
Дата публикации: 04.06.2020
Статья просмотрена: 53 раза
Библиографическое описание:
Абашкин, А. Н. Система кружковых занятий по решению японских головоломок для учащихся 5–6-х классов / А. Н. Абашкин. — Текст : непосредственный // Образование и воспитание. — 2020. — № 3 (29). — С. 44-48. — URL: https://moluch.ru/th/4/archive/168/5361/ (дата обращения: 20.04.2024).
Система дополнительного образования по математике часто направлена на выявление талантливых обучающихся. Поэтому такое образование предполагает подготовку учащихся к участию в различных математических олимпиадах. При этом, если сравнить количество учащихся (1 группа), желающих участвовать в олимпиадах, и количество учащихся (2 группа), успешно справляющихся с решением олимпиадных задач, то ни для кого не секрет, что в 5–6 классах количество учащихся 1 группы в разы превышает количество учащихся 2 группы. Диаграмма составлена по данным участия в школьном этапе учащихся филиала в 2019 году
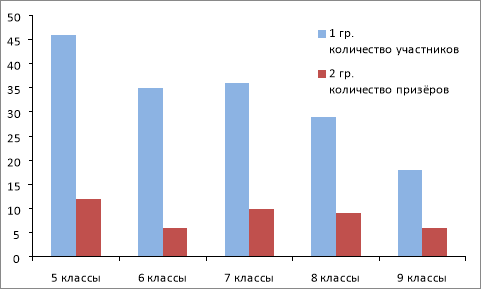
По диаграмме видно, что от класса к классу наиболее быстро убывает количество учащихся именно 1 группы. Здесь много причин, в том числе и формирование адекватной самооценки. Но немалую роль играет и падение интереса к решению нестандартных задач. Введение в систему дополнительного образования занятий, опосредованно связанных с математикой, поддерживает интерес учащихся к предмету, помогает расширить математический кругозор учащихся, не даёт потерять веру в свои силы. В первую очередь, говоря о таких занятиях, я имею в виду знакомство учащихся с миром головоломок, как механических (кубик Рубика разных размерностей и др.), так и аналитических.
К наиболее популярным аналитическим головоломкам сейчас можно отнести те, которые печатаются в развлекательных журналах — судоку и нонограммы. Но эти журналы, в основном, интересуют лишь взрослую аудиторию. Задания в таких изданиях рассчитаны на сосредоточенную длительную кропотливую работу, умение добиваться поставленной цели, а иногда и умения отступиться, признать своё поражение. В периодических изданиях, адресованных детям, таких головоломок практически нет.
В этом учебном году коллективом моих единомышленников была разработана система занятий математического кружка для 5–6 классов «Японские головоломки», где, начиная с азов, подробно рассматривается решение таких японских головоломок, как судоку, какуро, нонограмма.
Остановлюсь наиболее подробно на занятиях, посвящённых решению нонограмм. К нонограммам или японским кроссвордам относят рисунки на клетчатой бумаге, зашифрованные с помощью цифр.
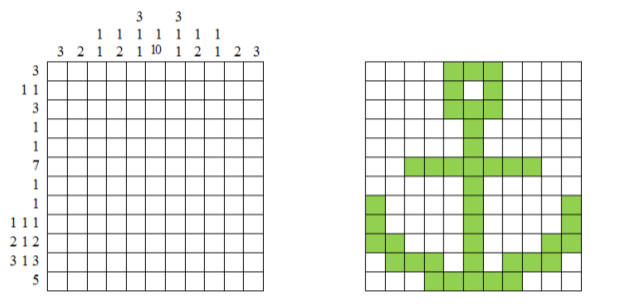
Для решения нонограммы используются два способа — аналитический и метод «от противного». В начале учебного года было проведено тестирование учащихся 5–9 классов на предмет умения решать нонограммы. Учащимся для решения была предложена простейшая нонограмма. В результате выяснилось, что в училище только один девятиклассник знает о существовании таких головоломок. Для сравнения: на момент исследования кубик Рубика размерностью 3х3 только среди 160 учащихся 5–6 классов умеют собирать 42 ученика. И их количество постоянно растёт! Такой результат связан, конечно, не с трудностью решения нонограмм, а с их малой распространённостью среди подростков.
Аналитический метод решения предусматривает нахождение закрашенных и пустых клеток. Рассмотрим основные аналитические методы решения.
Есть строки (столбцы), в которых можно сразу расположить закрашенные клетки, так как такое расположение единственно:
|
2 4 3 |
|||||||||||
|
|
|||||||||||
|
2 4 3 |
Есть строки (столбцы), в которых можно выделить клетки, являющиеся точно закрашенными. Например, блок из пяти клеток может располагаться в строке одним из четырёх способов, но при любом способе две центральные клетки будут закрашенными, так как блок должен быть хотя бы на одну клетку длиннее половины строки:
|
5 |
||||||||
|
|
||||||||
|
|
|
Если в строке (столбце) два блока клеток, то розовым цветом выделим область перемещения для первого блока из четырёх клеток:
|
4 3 |
И здесь можно выделить всегда закрашенную клетку:
|
4 3 |
Жёлтым цветом выделим область перемещения второго блока из трёх клеток:
|
4 3 |
Здесь нет клеток, закрашенных при любом положении блока. В результате решение такой строки (столбца) выглядит так:
|
4 3 |
Если удалось закрасить клетки в крайних строках (столбцах), то это даёт возможность закрасить некоторые клетки в столбцах (строках) и определить пустые клетки (отмечены точками):
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
|
3 2 |
||||||||
|
|
||||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
|
3 2 |
||||||||
|
· |
· |
|||||||
|
· |
· |
· |
Иногда удаётся выделить пустые клетки, если можно доказать, что блок закрашенных клеток до них не дойдёт:
|
4 |
· |
|
|
· |
· |
· |
могут быть закрашены
После знакомства с основными аналитическими методами обучающимся предлагается выполнить практическую работу № 1.
Определите в каждой строке (если это возможно) закрашенные или пустые клетки:
|
1) |
8 |
|
|
|
|
|
|
|
2) |
10 |
|
|
|
|
|
|
|
3) |
7 |
|
|
|
|
|
|
|
4) |
6 |
|
|
|
|
|
|
|
5) |
7 |
|
|
|
|
|
|
|
|
|
|
6) |
74 |
|
|
|
|
|
|
|
|
|
7) |
37 |
|
|
|
|
|
|
|
|
|
8) |
29 |
|
|
|
|
|
|
|
|
|
|
9) |
77 |
|
|
|
|
|
|
|
|
|
|
10) |
437 |
|
|
|
|
|
|
|
|
|
|
|
11) |
6 |
|
|
|
|
|
|
|
|
|
|
12) |
6 |
|
|
|
|
|
|
|
|
|
|
13) |
57 |
|
|
|
|
|
|
|
|
14) |
8 |
|
|
|
|
|
|
|
|
15) |
64 |
|
|
|
|
|
|
|
|
|
16) |
4 |
|
|
|
|
17) |
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
2 |
3 |
1 |
3 |
3 |
1 |
2 |
2 |
|
18) |
6 |
|
|||||||
|
|
3 |
|
|||||||
|
|
2 |
|
|||||||
|
|
4 |
|
|||||||
|
|
2 |
При выполнении этой работы автоматизируются навыки решения нонограмм. Затем учащимся предлагается выполнить четыре практических работы, в которых нонограммы расположены в порядке увеличения трудности решения.
Знакомство с методом «от противного» происходит на этапе, когда обучающиеся уже научились решать простые нонограммы небольшой размерности. Метод «от противного» предполагает, что какая-либо клетка (или группа клеток) закрашена, и, продолжив решение, приходим к противоречию, либо убеждаемся, что закраска была правильной.
|
3 |
1 1 |
4 1 1 |
6 3 |
4 1 1 |
1 1 |
3 |
|
|
1 |
· |
· |
· |
· |
· |
· |
|
|
3 |
· |
· |
· |
· |
|||
|
3 |
· |
· |
· |
· |
|||
|
1 3 1 |
· |
· |
|||||
|
1 3 1 |
· |
· |
|||||
|
1 1 1 |
· |
· |
· |
· |
|||
|
1 1 |
· |
· |
|||||
|
3 |
· |
· |
|||||
|
1 |
· |
· |
· |
· |
· |
· |
|
|
5 |
· |
· |
Например, если закрасить три клетки слева, отмеченные крестиками, то тогда в строке сверху невозможно разместить две единичные клетки. Если попробовать такую же группу клеток слева, то придём к такому же выводу. Значит, эта группа клеток будет закрашена по центру:
|
3 |
1 1 |
4 1 1 |
6 3 |
4 1 1 |
1 1 |
3 |
|
|
1 |
· |
· |
· |
· |
· |
· |
|
|
3 |
· |
· |
· |
· |
|||
|
3 |
· |
· |
· |
· |
|||
|
1 3 1 |
· |
· |
|||||
|
1 3 1 |
· |
· |
|||||
|
1 1 1 |
· |
· |
· |
· |
|||
|
1 1 |
· |
· |
· |
· |
· |
||
|
3 |
· |
· |
· |
· |
|||
|
1 |
· |
· |
· |
· |
· |
· |
|
|
5 |
· |
· |
Решение нонограмм также даёт и простор для собственного творчества обучающихся. Создание собственных нонограмм — это не просто творческий процесс, ведь необходимо не только придумать красивый рисунок и зашифровать его с помощью цифр, но и проверить, действительно ли при решении получившейся нонограммы получается задуманный рисунок, т. е. проверить нонограмму на единственность её решения.
Задавшись вопросом единственности решения, мы с обучающимися пришли к необходимости поиска факторов, влияющих на разрешимость нонограммы (т. е. на существование единственного решения этой головоломки). В результате обучающимися была проведена исследовательская работа по поиску этих факторов, результаты которой были представлены на научно-практических конференциях школьников разного уровня.
В числе факторов, влияющих на неразрешимость нонограмм, были определены разреженность рисунка нонограммы и использование внутри рисунка единичных квадратов в нонограмме (квадратов, в которых в каждой строке и каждом столбце закрашено по одной клетке).
В результате планомерной работы по решению нонограмм у учащихся постепенно формируется стойкий интерес к решению японских головоломок, а также нестандартных логических задач. Положительные эмоции, которые обучающиеся получают, разгадав очередную нонограмму, помогают им лишний раз увидеть свои возможности. Решение каждой следующей нонограммы — это преодоление себя, воспитания стремления добиваться поставленной цели, тренировка логического мышления.
В целом весь курс решения японских головоломок рассчитан на раскрытие и развитие как математического мышления и исследовательских способностей, так и других качеств личности — терпения, умения ставить цель и добиваться её достижения, умения критически анализировать свои действия и искать допущенные ошибки.
Похожие статьи
Методика работы над алгоритмической задачей в процессе...
надо | закрасить клетки ряда, левее каждой закрашенной. робот в исходном положении. Разработка алгоритма совместно с учениками
Перед стеной. Как закрасить клетки слева от уже данных? Сначала проверить закрашена ли клетка, затем сделать шаг влево, закрасить.
Система работы учителя математики по формированию навыков...
Одной из целей обучения является достижение такого уровня развития учащихся, когда они оказываются в силах самостоятельно ставить цель деятельности, актуализировать необходимые для решения задачи знания и способы деятельности; планировать свои...
Обучение решению арифметических задач | Статья в журнале...
В процессе решения арифметических задач учащиеся учатся планировать и контролировать свою деятельность, овладевать приёмами, самоконтроля (проверка задачи прикидка задач и т. д.) у них воспитывается настойчивость, воля, развивается интерес к поиску решения задачи.
Урок-мастерская как средство формирования самостоятельной...
Работа в группах (28 мин.) Каждая группа получает карточку с заданием, где указан метод решения и предложен чертеж, отражающий основную идею решения.
Представители групп выходят к доске и показывают решение, отвечают на вопросы одноклассников.
Обучение старших дошкольников решению арифметических задач
Ко второй группе относятся простые задачи, при решении которых надо осмысливать связь между компонентами и результатами арифметических
Как ответим на вопрос задачи? Запишите в своих тетрадях решение задачи с помощью цифр и арифметических знаков.
Особенности обучения младших школьников решению текстовых...
Решение задач вообще и математических в частности по своей сути — процесс творческий, требующий продуктивной, аналитической деятельности. В связи с этим возникли новые подходы при обучении младших школьников решению арифметических задач с применением...
Основные методы построения магических квадратов с нечетным...
Предлагаю вниманию читателя рассмотреть наиболее известные методы построения магических квадратов с нечетным числом клеток.
Числовым квадратом порядка n, где n – некоторое положительное целое число, мы будем называть квадрат, разбитый на n2 клеток, в...
Числовые ребусы как средство развития логического мышления
Как правило, головоломки считают одним из разделов занимательной математики. Это связано не только с тем, что практически любая
Головоломки специально предназначены для умственного развития детей и подростков, формирования логического мышления, они...
Ситуационная задача как один из современных методических...
Решение таких задач в конечном итоге приведет к развитию мотивации учащихся к познанию окружающего мира, освоению социокультурной среды; к актуализации предметных знаний с целью решения личностно — значимых проблем на деятельностной основе.
Решение нестандартных задач по математике с использованием...
Программа внеурочного курса «Решение нестандартных задач по математике» для учащихся 5 классов является расширением знаний предмета «математика» и рассчитана на 34 часа. Цель: формирование всесторонне образованной личности, умеющей ставить цели, организовывать...
Похожие статьи
Методика работы над алгоритмической задачей в процессе...
надо | закрасить клетки ряда, левее каждой закрашенной. робот в исходном положении. Разработка алгоритма совместно с учениками
Перед стеной. Как закрасить клетки слева от уже данных? Сначала проверить закрашена ли клетка, затем сделать шаг влево, закрасить.
Система работы учителя математики по формированию навыков...
Одной из целей обучения является достижение такого уровня развития учащихся, когда они оказываются в силах самостоятельно ставить цель деятельности, актуализировать необходимые для решения задачи знания и способы деятельности; планировать свои...
Обучение решению арифметических задач | Статья в журнале...
В процессе решения арифметических задач учащиеся учатся планировать и контролировать свою деятельность, овладевать приёмами, самоконтроля (проверка задачи прикидка задач и т. д.) у них воспитывается настойчивость, воля, развивается интерес к поиску решения задачи.
Урок-мастерская как средство формирования самостоятельной...
Работа в группах (28 мин.) Каждая группа получает карточку с заданием, где указан метод решения и предложен чертеж, отражающий основную идею решения.
Представители групп выходят к доске и показывают решение, отвечают на вопросы одноклассников.
Обучение старших дошкольников решению арифметических задач
Ко второй группе относятся простые задачи, при решении которых надо осмысливать связь между компонентами и результатами арифметических
Как ответим на вопрос задачи? Запишите в своих тетрадях решение задачи с помощью цифр и арифметических знаков.
Особенности обучения младших школьников решению текстовых...
Решение задач вообще и математических в частности по своей сути — процесс творческий, требующий продуктивной, аналитической деятельности. В связи с этим возникли новые подходы при обучении младших школьников решению арифметических задач с применением...
Основные методы построения магических квадратов с нечетным...
Предлагаю вниманию читателя рассмотреть наиболее известные методы построения магических квадратов с нечетным числом клеток.
Числовым квадратом порядка n, где n – некоторое положительное целое число, мы будем называть квадрат, разбитый на n2 клеток, в...
Числовые ребусы как средство развития логического мышления
Как правило, головоломки считают одним из разделов занимательной математики. Это связано не только с тем, что практически любая
Головоломки специально предназначены для умственного развития детей и подростков, формирования логического мышления, они...
Ситуационная задача как один из современных методических...
Решение таких задач в конечном итоге приведет к развитию мотивации учащихся к познанию окружающего мира, освоению социокультурной среды; к актуализации предметных знаний с целью решения личностно — значимых проблем на деятельностной основе.
Решение нестандартных задач по математике с использованием...
Программа внеурочного курса «Решение нестандартных задач по математике» для учащихся 5 классов является расширением знаний предмета «математика» и рассчитана на 34 часа. Цель: формирование всесторонне образованной личности, умеющей ставить цели, организовывать...







