Построение формальной арифметики в рамках изучения аксиоматических теорий в вузе



В статье «Аксиоматические теории в курсе математической логики» [1] рассматривается вопрос построения формальных и неформальных аксиоматических теорий.

В данной статье будет рассмотрен вопрос построения арифметики как формальной аксиоматической теории.

Формальная арифметика

Первое, полуаксиоматическое, построение арифметики было предложено в 1901 году Дедекиндом и стало известно под названием «система аксиом Пеано».

Аксиомы этой системы формулируются следующим образом:

1. 0 есть натуральное число.
2. Для любого натурального числа x существует другое натуральное число, обозначаемое x и называемое следующее за x.
3. 0  x для любого натурального числа x.
4. Если x = y, то x = y.
5. Если Q есть свойство, которым обладает натуральное число 0, и для всякого натурального числа x из того, что x обладает свойством Q,следует, что и натуральное число x обладает свойством Q, то свойством Q обладают все натуральные числа.

Пятую аксиому принято называть принципом индукции.

Этих аксиом достаточно для построения не только арифметики натуральных чисел, но и для построения теорий рациональных, вещественных и комплексных чисел.

Однако эта система аксиом содержит такое интуитивное понятие, как «свойство», что не позволяет ей быть формальной аксиоматической теорией.

Для формализации теорий, подобных арифметике, в математической логике используют формальные аксиоматические теории первого порядка сравенством.

Теория первого порядка называется теорией первого порядка сравенством, если она содержит предикатную букву , для которой следующие формулы являются аксиомами:

1. .

2. , где — произвольная формула.

Для сокращения вместо пишут t = s и тогда аксиомы принимают вид:

1. .

2. , где — произвольная формула.

Для вывода всех основных результатов элементарной арифметики была построена теория первого порядка S.

Эта теория первого порядка с равенством имеет единственную предикатную букву , единственную предметную константу a₁итри функциональные буквы .

Используя обозначения неформальной арифметики, пишут t = s вместо ,

0 вместоa₁иt, t + s, ts вместо соответственно.

Теория S имеет следующие собственные аксиомы:

1. .
2. .
3. .
4. .
5. .
6. .
7. .
8. .
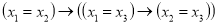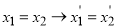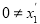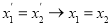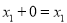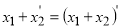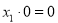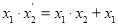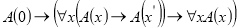9. , где 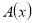— произвольная формула теории S.

Девятую аксиому принято называть принципом математической индукции.

Эта аксиома не соответствует пятой аксиоме системе аксиом Пеано, так как в системе аксиом Пеано интуитивно предполагается, что мощность множества свойств натуральных чисел — континуум, а в девятой аксиоме теории S может рассматриваться только счетное число свойств натуральных чисел, так как теория S — теория первого порядка [2].

С помощью правила отделения из девятой аксиомы получается следующее правило индукции: из и выводится.

Рассмотрим интерпретацию теории S, в которой:

1. Областью служит множество всех неотрицательных чисел.
2. Целое число 0 интерпретирует символ a₁.
3. Операция взятия следующего (то есть прибавление единицы) интерпретирует функциональную букву.
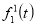4. Сложение и умножение интерпретируют функциональные буквы.
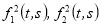5. отношение тождества интерпретирует предикатная буква .

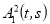Если считать истинность аксиом теории S в этой интерпретации интуитивно очевидной, то эта интерпретация является моделью теории S. Эта модель называется стандартной моделью теории S.

Термы 0;0;0;0;…в теории S называют цифрами и обозначают соответственно 0; ; ; ;…, то есть 0 с nштрихами обозначают .

В теории S можно ввести отношение порядка и понятие делимости. Далее можно показать, что теоремы, доказываемые в курсах элементарной теории чисел можно перевести на язык теории S и построить вывод полученной теоремы.

Для сокращения утверждения: «A есть теорема теории S» применяют запись .

Арифметические функции иарифметические отношения

Для изучения основных свойств теории S — непротиворечивостииполноты — используют арифметические функции и арифметические отношения, которые являются понятиями стандартной модели теории S.

Арифметическими функциями называются функции, у которых область определения и множество значений состоит из натуральных чисел.

Арифметическими отношениями называются отношения, заданные на множестве натуральных чисел.

Например, умножение — арифметическая функция с двумя аргументами, а выражение x + y < z является арифметическим отношением с тремя аргументами.

Арифметическое отношение R(x₁,…, x_n) называется выразимым в теории S, если существует формула A(x₁,…, x_n) теории S с n свободными переменными такая, что для любых натуральных чисел k₁,…, k_n выполняются условия: если R(k₁,…, k_n)истинно, то и если R(k₁,…, k_n)ложно, то.

В теориях первого порядка с равенством выражения вида «существует один и только один x такой, что A(x)» символически можно записать так: , для сокращения используют запись .

Арифметическая функция f(x₁,…, x_n) называется представимой в теории S, если существует формула A(x₁,…, x_n+1) теории S со свободными переменными x₁,…, x_n+1 такая, что для любых натуральных чисел k₁,…, k_n+1 выполняются условия:

1. Если f(k₁,…, k_n) = k_n+1, то .
2. .

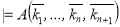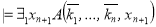Арифметическая функция f(x₁,…, x_n) называется сильно представимой в теории S, если существует формула A(x₁,…, x_n+1) теории S со свободными переменными x₁,…, x_n+1 такая, что для любых натуральных чисел k₁,…, k_n+1 выполняются условия:

1. Если f(k₁,…, k_n) = k_n+1, то .
2. .

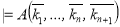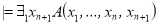Характеристической функцией отношения R(x₁,…, x_n) называется функция

C_R(x₁,…, x_n), которая равна 1, если отношение R(x₁,…, x_n) истинно, и равна 0, если отношение R(x₁,…, x_n) ложно.

Теорема. Если отношение R(x₁,…, x_n) выразимо в теории S, то характеристическая функция C_R(x₁,…, x_n) этого отношения сильно представима в теории S, а если характеристическая функция C_R(x₁,…, x_n)отношения R(x₁,…, x_n)представима в теории S, то в теории S выразимо отношение R(x₁,…, x_n).

При изучении представимости арифметических функций в теории S в качестве простейших функций выбраны следующие функции:

1. Нуль-функция: Z(x) = 0 при всех x.
2. Прибавление единицы: N(x) = x + 1 при всех x.
3. Проектирующие функции: 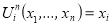при всех x₁,…, x_n, i = 1,…, n.

Для получения новых функций из простейших используют операции: суперпозиция функций, схема примитивной рекурсии и операция минимизации (-оператор).

Если f(x₁,…, x_n) = g(h₁(x₁,…, x_n), …, h_m(x₁,…, x_n)), то говорят, что функция f(x₁,…, x_n) получена с помощью операции суперпозиции из функций g(y₁,…, y_m), h₁(x₁,…, x_n), …, h_m(x₁,…, x_n).

Если f(x₁,…, x_n, 0) = g(x₁,…, x_n) и f(x₁,…, x_n, y + 1) = h(x₁,…, x_n, y, f(x₁,…, x_n, y)) то говорят, что (n + 1)-местная функция f получена с помощью схемы примитивной рекурсии из n-местной функции g и (n + 2)-местной функции h.

Функция f(x₁,…, x_n)называется примитивно рекурсивной, если она может быть получена из исходных функций с помощью конечного числа суперпозиций функций и схем примитивной рекурсии.

Обозначим через y [g₁(x₁,…, x_n, y) = g₂(x₁,…, x_n, y)] наименьшее значение y, при котором g₁(x₁,…, x_n, y) = g₂(x₁,…, x_n, y).

Если f(x₁,…, x_n) = y [g₁(x₁,…, x_n, y) = g₂(x₁,…, x_n, y)],то говорят, что функция f(x₁,…, x_n) получена из функций g₁(x₁,…, x_n, y) и g₂(x₁,…, x_n, y)спомощью операции минимизации (-оператора).

Функция f(x₁,…, x_n)называется частично рекурсивной, если она может быть получена из исходных функций с помощью конечного числа суперпозиций функций, схем примитивной рекурсии и операций минимизации.

Функция f(x₁,…, x_n)называется общерекурсивной или рекурсивной, если она частично рекурсивна и всюду определена.

Доказано, что класс рекурсивных функций совпадает с классом функций представимых в теории S [2].

Отношение R(x₁,…, x_n)называется примитивно рекурсивным, если примитивно рекурсивной является его характеристическая функция C_R(x₁,…, x_n).

Отношение R(x₁,…, x_n)называется рекурсивным, если рекурсивной является его характеристическая функция C_R(x₁,…, x_n).

В теориях первого порядка с равенством для сокращенной записи выражений вида «При всяком y, если y < z, то R(x₁,…, x_n, y)» используют запись .Ваналогичном смысле употребляются выражения , , .

Выражения, , , называются ограниченными кванторами.

Для отношений R(x₁,…, x_n, y)операция минимизации (-оператор) определяется следующим образом: через y [R(x₁,…, x_n, y)]обозначаютнаименьшее значение y,при котором отношение R(x₁,…, x_n, y)истинно.

Выражения и называются ограниченными -операторами и обозначают наименьшее значение y < z(соответственно y  z), при котором отношение R(x₁,…, x_n, y)истинно.

Теорема. Отношения, которые можно получить из примитивно рекурсивных (рекурсивных) отношений с помощью логических связок и ограниченных кванторов, также примитивно рекурсивны (рекурсивны).

Теорема. Применение ограниченных -операторов к примитивно рекурсивным (рекурсивным) отношениям приводит к примитивно рекурсивным (рекурсивным) отношениям.

Теорема. Всякаярекурсивная функция представима в теории S.

Теорема. Всякоерекурсивное отношение выразимо в теории S.

Гёделева нумерация формул ивыводов вформальной арифметике

В 1931 году Гёделем была предложена нумерация символов, выражений и конечных последовательностей теорий первого порядка с целью арифметизации метаматематики, то есть с целью замены утверждений о формальной системе эквивалентными высказываниями о натуральных числах.

Каждому символу u произвольной теории первого порядка ставится в соответствие положительное число g(u), называемое гёделевым номером символа u, следующим образом:

g(() = 3; g()) = 5; g(,) = 7; g() = 9; g() = 11;

g(x_k) = 5 + 8k, где k = 1, 2, …;

g(a_k) = 7 + 8k, где k = 1, 2, …;

для k, n  1;

для k, n  1.

Таким образом, различным символам поставлены в соответствие различные гёделевы номера, являющиеся положительными нечетными числами.

Например, g(x₂) = 5 + 82 = 21; g(a₄) = 7 + 84 = 39;; .

Гёделев номер выражения u₀u₁…u_r определяется следующим образом: , где p_i есть i-епростое число, при этом p₀ = 2.

Например,

Так как любое натуральное число единственным образом разлагается в произведение степеней простых чисел, то различные выражения получат разные гёделевы номера.

Гёделевы номера выражений четны и поэтому отличаются от гёделевых номеров символов.

Если символ рассматривать как выражение, то он будет иметь гёделев номер, отличный от того, который ставится ему в соответствие как символу.

Гёделев номер последовательности выражений e₀, e₁,…, e_r определяется следующим образом: , где p_i есть i-епростое число, при этом p₀ = 2.

Различные последовательности выражений имеют различные гёделевы номера, а так как они четны и имеют четный показатель степени при 2, то они отличны от гёделевых номеров символов выражений.

Таким образом, функция g взаимно однозначно отображает множество всех символов, выражений и конечных последовательностей выражений в множество целых положительных чисел.

Множество значений функции g не совпадает с множеством всех целых положительных чисел, например, число 12 не является гёделевым номером.

Теорема Гёделя онеполноте формальной арифметики

В формулировке теоремы о неполноте формальной арифметики Гёдель использовал понятие -непротиворечивой теории первого порядка, что представляет собой более сильное условие, чем просто непротиворечивость.

Теория первого порядка называется -непротиворечивой, если для всякой формулы A(x)этой теории из того, что при любом n, следует невозможность , другими словами для всякой формулы A(x) этой системы невозможно одновременно вывести формулы и .

Доказано, что -непротиворечивая теория первого порядка является непротиворечивой [2].

Если признать стандартную интерпретацию теории S в качестве модели этой теории, то тогда теорию S следует признать -непротиворечивой.

Для доказательства неполноты формальной арифметики используется примитивно рекурсивное отношение W₁(u, y)=«u есть гёделев номер формулы A(x₁), содержащей свободную переменную x₁, и y есть гёделев номер вывода в S формулы » [2].

Так как отношение W₁(u, y) примитивно рекурсивно, то оно выразимо в теории S некоторой формулой V₁(x₁, x₂) с двумя свободными переменными x₁, x₂. Значит, если W₁(k₁, k₂) истинно, то , и если W₁(k₁, k₂) ложно, то .

Рассмотрим формулу . Пусть m — гёделев номер этой формулы. Подставим в эту формулу вместо x₁, получим замкнутую формулу: .

Из определения W₁(u, y)следует, чтоW₁(m, y)истинно тогда и только тогда, когда y есть гёделев номер вывода в S формулы .

Теорема (Гёдель, 1931 год). Если теория S непротиворечива, то формула невыводима в теории S,иесли теория S -непротиворечива, то формула невыводима в теории S.

Доказательство

Предположим, что теория S непротиворечива и .

Пусть k — гёделев номер какого-либо вывода в S формулы .

Следовательно, справедливо отношение W₁(m, k). Так как V₁выражает W₁вS, то .

Из следует, что .

Таким образом, в теории S оказываются выводимыми формулы и , что противоречит предположению о непротиворечивости S.

Предположим, что теория S -непротиворечива и .

Из -непротиворечивости теории следует ее непротиворечивость и, следовательно, формула невыводима в теории S.

Поэтому никакое натуральное число n не является гёделевым номером вывода в S формулы , то есть отношение W₁(m, n)ложно для любого n, а это означает, что для любого n.

Возьмем в качестве формулы теории S формулу . Из предположения о -непротиворечивости теории S следует, что в теории S невыводима формула , что противоречит предположению. Теорема доказана.

Таким образом, в непротиворечивой теории S невыводимы как формула , так и ее отрицание .

Рассмотрим стандартную интерпретацию неразрешимого предложения .

Так как V₁ выражает в теории S отношение W₁, то, в соответствии со стандартной интерпретацией, формула утверждает, что отношение W₁(m, x₂) ложно для любого натурального числа x₂, а это означает, что не существует вывода формулы в теории S. Таким образом, формула утверждает свою собственную невыводимость в теории S.

Из теоремы Гёделя следует, что если теория S непротиворечива, то эта формула и в самом деле невыводима в теории S и поэтому истинна при стандартной интерпретации.

Итак, в стандартной интерпретации формула верна, но невыводима в теории S.

Это наводит на мысль, что теорема Гёделя справедлива потому, что для теории S выбранная система аксиом содержит недостаточно аксиом, и если добавить новые аксиомы, в частности истинную формулу , то можно получить новую теорию S₁, для которой теорема Гёделя, возможно, окажется неверной.

Однако, всякая рекурсивная функция, будучи представимой в теории S, будет также представима и в теории S₁, и отношение W₁(u, y) в теории S₁ будет являться примитивно рекурсивным, а этого достаточно для доказательства теоремы Гёделя.

Поэтому, если теория S₁ -непротиворечива, то она будет содержать неразрешимую формулу, отличающуюся от формулы , но имеющую такую же форму.

В теореме Гёделя содержится предположение о -непротиворечивости теорииS. Однако ценой некоторого усложнения доказательства можно ограничиться предположением об обычной непротиворечивости теории S.

В этом случае необходимо будет воспользоваться примитивно рекурсивным отношением W₂(u, y) = «u есть гёделев номер формулы A(x₁), содержащей свободную переменную x₁, и y есть гёделев номер вывода в S формулы » [2].

Так как, отношение W₂(u, y) примитивно рекурсивно, то оно выразимо в теории S некоторой формулой V₂(x₁, x₂) с двумя свободными переменными x₁, x₂. Значит, если W₂(k₁, k₂)истинно, то , и если W₂(k₁, k₂) ложно, то .

Рассмотрим формулу . Пусть n — гёделев номер этой формулы. Подставим в эту формулу вместо x₁ — получим замкнутую формулу: .

Теорема (Россер, 1936 год). Если теория S непротиворечива, то в ней невыводимы обе формулы и и, следовательно, существует неразрешимое предложение этой теории.

Эту теорему называют теоремой Гёделя в форме Россера.

Теорема Гёделя онепротиворечивости формальной арифметики

Рассмотрим вопрос о непротиворечивости теории S.

Для доказательства непротиворечивости формальной арифметики помимо отношений W₁(u, y) и W₂(u, y)используется примитивно рекурсивное отношение

Pf(y, x) = «y есть гёделев номер вывода в S формулы с гёделевым номером x»выразимое в теории S с помощью некоторой формулы Pf(x₁, x₂) [2].

Далее, если x — гёделев номер формулы A, то через Neg(x) обозначают гёделев номер формулы . Доказано, что функция Neg(x)рекурсивна и, следовательно, представима в теории S некоторой формулой Neg(x₁, x₂) [2].

Вторая теорема Гёделя. Если теория S непротиворечива, то в ней невыводима формула, утверждающая непротиворечивость теории S.

Доказательство

Формула в стандартной интерпретации выражает невозможность вывода в теории S какой-либо формулы вместе с ее отрицанием и является истинной в том и только том случае, когда теория S непротиворечива. Иными словами, эту формулу можно интерпретировать как утверждение непротиворечивости теории S.

В соответствии со стандартной интерпретацией, гёделева неразрешимая формула выражает свою собственную невыводимость.

Тогда формула утверждает, что если теория S непротиворечива, то формула в ней невыводима. То есть эта формула есть формальная запись первой части теоремы Гёделя.

Математические рассуждения, доказывающие теорему Гёделя, могут быть выражены и проведены средствами теории S, так что в результате оказывается возможным получить вывод формулы

в теории S [2].

Таким образом,.

Если , то по правилу отделения получаем, что .

Из теоремы Гёделя следует, что если теория S непротиворечива, то формула в ней невыводима. Следовательно, если теория S непротиворечива, в ней невыводима формула .

Таким образом, если теория S непротиворечива, то в ней невыводима формула, утверждающая непротиворечивость теории S.

Другими словами, если теория S непротиворечива, то доказательство непротиворечивости теории S не может быть проведеносредствами самой теории S.

Литература:

1. Сухан И. В., Кравченко Г. Г., Иванисова О. В. Аксиоматические теории в курсе математической логики // Педагогика высшей школы. — 2017. — № 3. — С. 28–38.
2. Мендельсон Э. Введение в математическую логику. — М.: Наука, 1976. — 320 с.