Одной из основных задач математической логики является изучение понятия правильного рассуждения, или доказательства.
Доказательство (в широком смысле этого слова) — это логическое действие, в процессе которого истинность какого-либо суждения обосновывается с помощью других суждений.
Любое неформальное рассуждение (доказательство) представляет собой конечную последовательность повествовательных предложений (то есть высказываний), приводимых в обоснование того, что последнее повествовательное предложение (высказывание) в этой последовательности может быть выведено из начальных повествовательных предложений (высказываний).
Таким образом, изучение теории доказательств целесообразно начать с методов алгебры высказываний.
В алгебре высказываний обычно приходится доказывать, что некоторое высказывание B является логическим следствием некоторых высказываний A1, A2, …, An(в символической записи A1, A2, …, An |= B). Для этого применяют две схемы доказательств: прямое доказательство и косвенное.
Прямое доказательство того, что A1, A2, …, An |= B проводят по следующей схеме:
- Формулы A1,A2, …,Anсчитают входящими в доказательство.
- К доказательству присоединяют ранее доказанные формулы, в частности тавтологии.
- К доказательству присоединяют новые формулы, полученные по правилам вывода.
- Доказательство закончено, если последняя формула есть B.
Эта схема обосновывается теоремой [5] о представлении доказательства в виде цепочки формул. Для доказательства этой теоремы требуется две леммы.
Лемма 1. A1, A2, …, An |=Ai, i = 1, 2, …, n.
Доказательство следует из определения логического следствия.
Лемма 2. Если A1, A2, …, An |= Bj, j = 1, 2, …, m, и если B1, B2, …, Bm |= C, то
A1, A2, …, An |= C.
Доказательство.
Доказательство проведем с помощью таблицы истинности высказываний Ai, Bj, C, построенной по переменным, входящим хотя бы в одну из формул Ai, Bj, C.
Рассмотрим строки таблицы, в которых все Ai принимают значение T (истина). Из определения логического следствия получаем, что все Bj в этих строках также получают значения T, следовательно, и C в этих строках принимает значение T, а это и означает, что A1, A2, …, An |= C.
Теорема о представлении доказательства в виде цепочки формул.
A1, A2, …, An |= B, если можно составить цепочку формул E1, E2, …, Em= B, в которой либо Ek = Aj, либо в этой цепочке есть предшествующие формулы ![]() такие, что
такие, что![]() .
.
Другими словами, каждая формула цепочки либо есть посылка, либо получена из предыдущих формул цепочки по одному из правил вывода.
Доказательство.
Пусть такая цепочка построена, Ek удовлетворяют условию теоремы, т. е. либо Ek= Aj, либо существуют предшествующие формулы![]() такие, что
такие, что![]() .
.
Докажем, что A1, A2, …, An|= Ek для k = 1…, m (Em = B). Доказательство проведем методом математической индукции.
При k = 1 имеем: предшествующих формул нет, значит E1 — одна из посылок, т. е. E1 = Ai для некоторого i= 1, 2, …, n. По лемме 1 имеем: A1, A2, …, An |= Ai= E1, i = 1, …, n.
Пусть это справедливо для E1, E2, …, Ek–1, т. е. A1, A2, …, An |= Ei, i= 1, …, k — 1.
Докажем, что это справедливо и для Ek.
Если Ek — посылка, то применима лемма 1. Если Ekпосылкой не является, то из условия теоремы следует, что ![]() и так, как
и так, как ![]() , то по предположению индукции A1, A2, …, An |=
, то по предположению индукции A1, A2, …, An |= ![]() , j = 1, …, s и по лемме 2 имеем:
, j = 1, …, s и по лемме 2 имеем:
A1, A2 …, An |= Ek.
Тогда A1, A2, …, An |= Ek для любого k = 1, …, m.
Замечание. Очевидно, что в цепочку можно включать любую тавтологию. Если |=D (D — тавтология), то для любой формулы A имеем |=A→D. В качестве формулы A можно взять любую посылку Ai, тогда |=Ai→ D или Ai |=D.
Косвенное доказательство (или доказательство от противного) того, что
A1, A2, …, An |= B проводят по следующей схеме:
- Формулы A1,A2, …,Anсчитают входящими в доказательство.
-
К доказательству присоединяют формулу
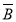 .
.
- К доказательству присоединяют ранее доказанные формулы, в частности тавтологии.
- К доказательству присоединяют новые формулы, полученные по правилам вывода.
-
Доказательство закончено, если в нем имеются две формулы
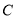 и
и 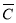 .
.
Для обоснования этой схемы нами была доказана следующая теорема.
Теорема (обоснование метода доказательства от противного).
A1, A2 …, An |= B, если из A1, A2, …, An, An+1 = ![]() можно составить цепочку формул E1, E2, …, Em в которую входят две формулы
можно составить цепочку формул E1, E2, …, Em в которую входят две формулы ![]() и
и ![]() , и в которой либо Ek = Aj, либо в этой цепочке есть предшествующие формулы
, и в которой либо Ek = Aj, либо в этой цепочке есть предшествующие формулы ![]() такие, что
такие, что![]() .
.
Доказательство.
Пусть такая цепочка построена.
После формул ![]() и
и ![]() вставим в цепочку тавтологию
вставим в цепочку тавтологию ![]() и применим правило отделения:
и применим правило отделения: ![]() Применим еще раз правило отделения
Применим еще раз правило отделения ![]() .
.
Таким образом, в цепочке появилась формула ![]() . По теореме о представлении доказательства в виде цепочки формул имеем
. По теореме о представлении доказательства в виде цепочки формул имеем
A1, A2 …, An, ![]() |=
|= ![]() . Отсюда получаем: A1, A2, …, An |=
. Отсюда получаем: A1, A2, …, An |= ![]() [5, с. 95].
[5, с. 95].
Рассмотрим такой набор переменных, входящих во все формулы, что все Aiпринимают значение T, тогда и ![]() = T.
= T.
Так, как ![]() = F, то и
= F, то и ![]() = F, а следовательно B = T, а это означает, что
= F, а следовательно B = T, а это означает, что
A1, A2, …, An |= B.
Замечание. Для присоединения к доказательству новых формул используют основные правила вывода алгебры высказываний [2]:
-
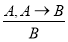 (правило отделения, правило заключения, modus ponens).
(правило отделения, правило заключения, modus ponens).
-
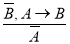 (правило отрицания, modus tollens).
(правило отрицания, modus tollens).
-
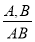 (правило введения конъюнкции).
(правило введения конъюнкции).
-
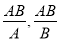 (правило удаления конъюнкции).
(правило удаления конъюнкции).
-
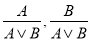 (правило введения дизъюнкции).
(правило введения дизъюнкции).
-
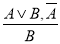 (правило удаления дизъюнкции).
(правило удаления дизъюнкции).
-
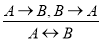 (правило введения эквиваленции).
(правило введения эквиваленции).
-
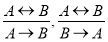 (правило удаления эквиваленции).
(правило удаления эквиваленции).
-
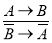 (правило контрапозиции).
(правило контрапозиции).
-
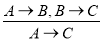 (правило цепного заключения, правило силлогизма).
(правило цепного заключения, правило силлогизма).
-
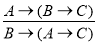 (правило перестановки посылок).
(правило перестановки посылок).
-
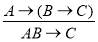 ,
, 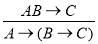 (правило объединения и разъединения посылок).
(правило объединения и разъединения посылок).
Литература:
- Успенский В. А., Верещагин Н. К., Плиско В. Е. Вводный курс математической логики. — М.: Физматлит, 2007. — 128 с.
- Игошин В. И. Математическая логика и теория алгоритмов. М.: Издательский центр «Академия», 2010. — 448 с.
- Колмогоров А. Н., Драгалин А. Г. Введение в математическую логику. М.: Издательство Московского университета, 1982. — 120 с.
- Мендельсон Э. Введение в математическую логику. — М.: Наука, 1976. — 320 с.
- Столл Р. Р. Множества. Логика. Аксиоматические теории. М.: Просвещение, 1968. — 232 с.

