Решение нестандартных задач по математике с использованием информационных технологий



Вид деятельности: познавательная

Форма: кружок

Направление воспитания: воспитание отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии

Направление развития личности: общеинтеллектуальное, общекультурное, социальное

Пояснительная записка

Обучение математике является важнейшей составляющей основного общего образования и призвано развивать логическое мышление и математическую интуицию учащихся, обеспечить овладение учащимися умениями в решении различных практических и межпредметных задач. Математика входит в предметную область «Математика и информатика». Основной целью учебного курса является обучение решению нестандартных задач по математике. Курс также закладывает пропедевтику наиболее значимых тем курса математики и позволяет успешно готовиться к участию в олимпиадах по предмету. Отдельные разделы предусматривают использование информационных технологий, что определено следующими целями:

– развитие личности обучаемого в условиях информационного общества;

– развитие алгоритмического мышления благодаря особенностям общения с компьютером;

– развитие творческого мышления за счет уменьшения доли репродуктивной деятельности;

– развитие навыков исследовательской деятельности;

– формирование информационной культуры.

Содержание курса строится на основе системно — деятельностного подхода.

Одной из особенностей творческой личности является устойчивое умение находить лучшее решение проблемы (творчество). Это относится к любым задачам. Множество нестандартных задач для учащихся основной школы сконцентрировано в математике. Научить решать нестандартные задачи — интересная, но и достаточно непростая работа. Решение нестандартных задач соотносится с творчеством личности. Поэтому чем больше учтено существенных элементов, входящих в процесс творчества, тем успешнее будет достигнута цель.

Для достижения указанной цели, прежде всего, необходимо познакомиться с идеями и механизмом, лежащими в основе творчества, необходимого для решения нестандартных задач, получить представление о новом подходе к обучению и познакомиться с методикой достижения значимых результатов. А далее на примере достаточно большого числа олимпиадных задач разобрать различные приемы решений, для которых вычленены и обобщены их особенности.

Так, прослеживая связь творческого процесса и процесса решения нестандартной задачи, рассматриваются компоненты творчества: научные знания, творческое мышление, умения творческой работы, а также такие качества, без которых немыслимо творчество: анализ, синтез и умение предвидеть, т. е. прогнозировать. Большое внимание необходимо уделять возрастным особенностям восприятия учебного материала учащимися, а также принципам организации занятий по развитию творческого мышления при решении нестандартных и олимпиадных задач у учащихся пятых классов.

В программе учитывается взаимосвязь репродуктивной и проблемной формы обучения, коллективной и самостоятельной работы. Используются активные и интерактивные формы учебного сотрудничества: «учитель-ученик», парная и групповая работа, что в свою очередь так же влияет на формирование знаний, умений, опыта творческой деятельности.

Практическое выполнение программы предполагает выполнение обучающимися творческих работ, проверочных работ, индивидуальных и коллективных проектов, практических занятий на компьютере, участие в играх, соревнованиях.

Программа внеурочного курса «Решение нестандартных задач по математике» для учащихся 5 классов является расширением знаний предмета «математика» и рассчитана на 34 часа.

Цель: формирование всесторонне образованной личности, умеющей ставить цели, организовывать свою деятельность, оценивать результаты своего труда, применять математические знания в жизни.

Задачи:

1. Создание условий для реализации математических и коммуникативных способностей подростков в совместной деятельности со сверстниками.
2. Формирование у младших подростков навыков применения математических знаний для решения различных жизненных задач.
3. Развитие математической и информационной культуры школьников, логического мышления, памяти, воображения, любознательности; умения самостоятельно приобретать, анализировать и применять математические знания на практике.
4. Формирование представлений о компьютере как универсальном устройстве обработки информации; развитие основных навыков и умений использования компьютерных устройств.

Таблица 1

Учебно-тематический план

№п/п	Тема	Количество часов	Форма проведения
1	Числа и вычисления	5	Эвристическая беседа Работа в группах Защита групповых проектов «Счет у древних людей», «Меры длины, веса, площади» Практическое занятие «Римские цифры»
2	Геометрические задачи	4	Практические занятия Математическая лаборатория «Моделирование с использованием УМК «Живая математика». Индивидуальный проект «Алгоритмы чертежей в программе «Живая математика»
3	Развивающие и логические задачи	7	Самостоятельная работа по сценарию. Практические занятия на компьютерах с использованием УМК «Живая математика». Решение задач на переливания, переправу. Индивидуальные проекты. Викторина «Математическая смесь»
4	Задачи на движение	7	Практические занятия с использованием компьютерной среды ИИСС «Математика на компьютерах». Задачи на движение в одном направлении, в противоположных направлениях, по течению, против течения
5	Олимпиадные задачи	11	Обсуждения, дискуссии. Работа в группах. Исследовательская работа. Проблемно-поисковая работа. Игра «Эстафета» Мини-олимпиада

Содержание тем

Тема 1. Числа ивычисления(6 часов)

Счёт у первобытных людей. О происхождении арифметики. Происхождение и развитие письменной нумерации. Арифметика Магницкого. Метрическая система мер. Измерения в древности у разных народов. Старые русские меры. Происхождение дробей. Дроби в Древней Греции, в Древнем Египте. Нумерация и дроби на Руси. Восстановление цифр при сложении, вычитании, умножении. Решение задач на отгадывание чисел. Комбинации в расположении. Магические квадраты.

Тема 2. Геометрические задачи (6 часов)

Геометрия на клетчатой бумаге. Задачи на разрезание фигур на равные части. Алгоритмы чертежей и измерения в программе «Живая математика». Построение квадрата, треугольников, прямоугольника, ромба, правильного шестиугольника. Измерение длин отрезков, углов, площадей и периметров геометрических фигур.

Тема 3. Развивающие илогические задачи (7 часов)

Логические задачи. Задачи со спичками. Задачи на переливание. Задачи на переправу. Задачи на взвешивание. Графы в решении задач. Принцип Дирихле. Задачи из книги Магницкого. Викторина «Математическая смесь».

Тема 4. Задачи на движение (7 часов)

Работасиспользованиемкомпьютерной среды ИИСС «Математика на компьютерах».

Задачи на движение в одном направлении. Задачи на движение навстречу друг другу. Задачи на движение по течению и против течения.

Тема 5. Олимпиадные задачи (8 часов)

Практикум порешению олимпиадных задач школьного, муниципального и регионального уровней.

Контрольно-измерительные материалы

Игра «Эстафета».

Практическая работа на разрезание геометрических фигур на равные части

Защита групповых проектов «Счет у древних людей», «Меры длины, веса, площади».

Индивидуальные проекты «Алгоритмы чертежей в программе «Живая математика».

Индивидуальней проекты «Задачи на движение» с использованием компьютерной среды ИИСС «Математика на компьютерах».

Викторина «Математическая смесь».

Мини олимпиада.

Мини-олимпиада

1. Переложите в каждом равенстве по одной спичке так, чтобы равенства стали верными:

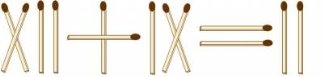
Рис. 1. Задачи со спичками

2. Разрежьте фигуру по линиям сетки на три одинаковые части:

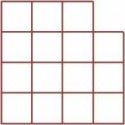
Рис. 2. Задача на разрезание

3. Требуется построить ломаную из четырех звеньев, проходящую через все девять точек. Возможно ли это?

Рис. 3. Задача на построение ломаной

4. Разбейте циферблат часов с помощью отрезков на три части таким образом, чтобы сумма чисел в каждой из этих частей была одной и той же:

Рис. 4. Задача с часами

5. Расставьте скобки и знаки математических действий так, чтобы получилось верное равенство:

9 9 9 9 9 9 9 = 100

6. Найдите цену чашки и цену блюдца.

Рис. 5. Задача о чашке и блюдце

7. Подряд стоят 6 стаканов: 3 с водой и 3 пустых. Как с помощью одного из этих стаканов сделать так, чтобы стаканы чередовались пустые и с водой?

Рис. 6. Задача о стаканах

8. Даны числа 1, 2, 3, 4, 5, 6, 7, 8, 9. Расставьте их так, чтобы сумма их на каждой стороне треугольника была равна 20.

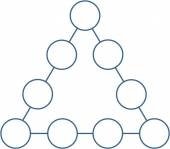
Рис. 7. Задача о треугольнике

Литература:

1. И. Я. Депман, Н. Я. Виленкин. «За страницами учебника математики: Пособие для учащихся 5–6 классов сред школ. — М.: «Просвещение», 1989 г.
2. «Все задачи «Кенгуру»», С-П., 2003г.
3. Нагибин, Ф.Ф., Канин, Е. С. Математическая шкатулка [Текст]: Пос. для уч-ся.- [Изд. 4-е, перераб. и доп.].- М.: Просвещение, 1984.
4. Олимпиадные задания по математике. 5–8 классы. 500 нестандартных задач для проведения конкурсов и олимпиад: развитие творческой сущности учащихся [Текст] /Автор — сост. Н. В. Заболотнева.- Волгоград: Учитель, 2006.
5. Онучкова, Л. В. Введение в логику. Логические операции [Текст]: Учеб.пос. для 5 класса.- Киров: ВГГУ, 2004.
6. Б. А. Кордоменский, «Математическая смекалка», учебное пособие для 5–6 классов общеобразовательных учреждений.
7. Нагибин, Ф.Ф., Канин, Е. С. Математическая шкатулка [Текст]: Пос. для уч-ся.- [Изд. 4-е, перераб. и доп.].- М.: Просвещение, 1984.
8. Интернет ресурсы: https://infourok.ru; http://geo.1september.ru; School-collection.edu.ru;
9. М. В. Васильева. Использование информационных технологий при обучении математике. Учебно-методическое пособие. АСОУ.2015.