В статье рассматриваются преобразования Хартли и Фурье, рассматриваются их зависимости. Рассмотрены сходства и отличия преобразования Хартли и Фурье.

Ключевые слова:преобразование Хартли, преобразование Фурье, cas функция, действительная и мнимая часть.

Ральф Винтон ЛайонХартли, раскрыл вещественные преобразования тесно связанные с преобразованием Фурье в 1942 году. Кроме того, используя собственные свойства, преобразование введенное Хартли позволяет произвести расчёты косвенных вычислений спектра мощности Фурье данной функции, пользуясь только арифметикой. В последние десятилетия были предложены некоторые новые дискретные вещественные ортогональные преобразования, которые Хартли, связал с другим известным комплексом.

В 1942 году было опубликована статья об интегральных преобразованиях — прямом и обратном, использующие введенную Хартли функцию 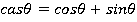. Преобразование Хартли позволяет разложить функцию на два синусоидальных компонента как набора представленных с точки зрения положительных и отрицательных составляющих отличающихся простотой от сложных геометрических прогрессий exp(jɷx), используемых в классическом анализе Фурье.

В отличие от преобразования Фурье, преобразование Хартли трансформирует одни вещественные функции в другие вещественные же функции не используя мнимую часть функции. Дискретная версия преобразования Хартли, была введена R. N.Bracewell в 1983 году [1, с.114].

Преобразование Хартли функции f(t) определяется:

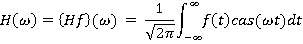
Где ɷ может быть угловой частотой и 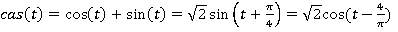это косинус и синус или ядро Хартли. С инженерной точки зрения, это преобразование принимает сигнал (функцию) из временной области в спектральной области Хартли.

Преобразование Хартли (как преобразование Фурье) имеют различные мелкие детали являющиеся предметом конвекции и могут быть изменены без изменения основных свойств.

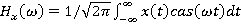 — Прямое преобразование.

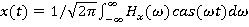 — Обратное преобразование.

1)                 Вместо того что бы использовать одно и тоже преобразование для прямого и обратного, можно удалить 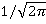 из прямого преобразования и использовать 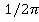для обратного преобразования и вынести такой же коэффициент из прямого преобразования.

2)                 Можно также использовать 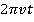 вместо  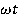(т. е. частота вместо угловой частоты), в этом случае коэффициент  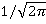полностью опустится.

3)                 Можно использовать разность cosɵ — sinɵ вместо cosɵ+ sinɵ [2, с.15]

Связь с преобразованием Фурье.

Преобразование Хартли отличается от классического преобразования Фурье F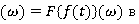выборе ядра. В преобразование Фурье, экспоненциальное ядро:  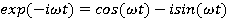где i — это мнимая единица.

Эти два преобразования тесно связаны между собой, однако преобразование Фурье (при условие, что преобразование использует коэффициент 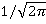 нормализации конвенции) может быть вычислено из преобразования Хартли:

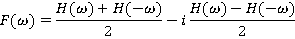
То есть, действительная и мнимая часть преобразования Фурье задаётся чётными и нечётными частями преобразования Хартли. И наоборот, для вещественной функции F(T), преобразования Хартли задаётся от преобразования Фурье, действительной и мнимой частью.

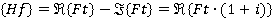
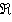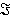Где  и  обозначают действительную и мнимую часть комплексного преобразования Фурье.

Пример преобразования Хартли и Фурье.

T=4,t=0.01..T, s(t)=exp [-5(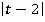)²],

cas(x)=cos(x)+sin(x) 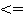Функции Хартли.

Sh(f)=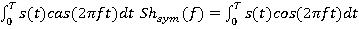

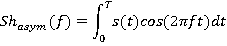
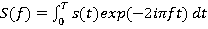 F=1.5 f=-F,_f+0.02.. F

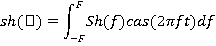
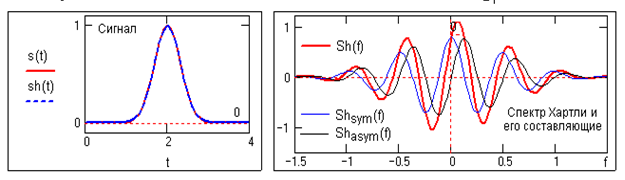
Сопоставление составляющих спектра Хартли с действительной и мнимой частью спектра Фурье [3].

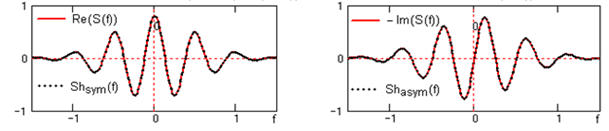
Свойства преобразования.

Преобразование Хартли — это линейный оператор (преобразование Фурье также относится к линейным интегральным операциям) Из симметричности и обратных свойств, преобразование является унитарным оператором (в самом деле, ортогональном).

Существует также аналог теоремы свёртки для преобразования Хартли. Если две функции х(t) и y(t) имеют преобразование Хартли X(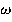) и 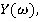то их свёртки  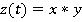есть преобразование Хартли:

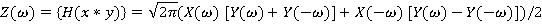
По аналогии с преобразованием Фурье, преобразование Хартли чётной/нечётной функции чётные/нечётные.

CASфункция.

Свойства cas функции вытекают непосредственно из тригонометрии, и его определение как фазовый сдвиг тригонометрических функции

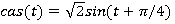то:

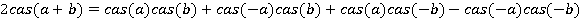
кроме того:

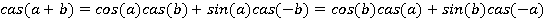
и её производная равна:

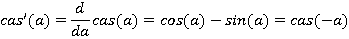
Преобразование Хартли может использоваться в качестве альтернативы преобразования Фурье при учете вышеописанных свойств.

Литература:

1.      Злобин С.Л, Стальной А. Я. «Двумерное быстрое преобразование Хартли в цифровой обработке изображений». Доклады 6–ой Международной конференции «Цифровая обработка сигналов и её применение». Том 2, стр. 114–116. Труды РНТОРЭС им. А. С. Попова. Москва, Россия, 2004 г.

2.      Брейсуэлл Р. Преобразование Хартли. Теория и приложения. — М.: Мир, 1990

3.      Bracewell, Ronald.N. (1986). The Hartley Transform. Oxford University Press. ISBN 9780195039696

4.      Poularikas A. D. «The Hartley Transform» The Handbook of Formulas and Tables for Signal Processing. Ed. Alexander D. Poularikas Boca Raton: CRC Press LLC,1999