Реакция рекурсивной ЛДС с передаточной функцией в виде суммы простых дробей 1-й степени на апериодическое воздействие.

Микропроцессорные реле имеют много особенностей по сравнению с электронными в части, касающейся обработки аналоговых сигналов, цифровой фильтрации преобразованных аналоговых сигналов, построения измерительных органов, каналов передачи данных и т. д.

Измерительные органы устройств релейной защиты, в которых при обработке информации выполняются операции с последовательностями чисел, зависящими от текущих значений входных напряжений и токов, являются цифровыми — ЦИО. Использование цифровой обработки сигналов и соответствующих методов их преобразования обусловливает новые свойства ЦИО, отсутствующие у аналоговых РИО, что требует учёта их при проектировании современных микропроцессорных комплексов РЗА. Для оценки поведения ЦИО в реальных режимах работы электрической системы необходимы исследования методов реализации их характеристик, влияния частоты дискретизации входных сигналов на характеристики ЦИО, частотных характеристик ЦИО, поведения их в динамических условиях и т. д.

В процессе цифровой обработки мгновенных значений вторичных токов и напряжений входных преобразователей, представляющих собой «смесь» полезного сигнала и помех, возникает задача «очистки» сигнала промышленной частоты от всех иных составляющих, которые в общем случае содержат апериодическую слагаемую, слагаемые 3-й и 5-й гармоник, влияние которой особенно сильно сказывается в фильтровых и дифференциальных реле, а также другие высшие гармоники. Указанная задача решается, хотя и не полностью, цифровыми фильтрами, под которыми в общем смысле понимают цифровую систему, осуществляющую по заданному алгоритму выделение цифрового сигнала x(nT_д) или его параметров из его воздействия x_S(nT_д)x(nT_д)x_помs(nT_д), содержащего суммарную помеху x_s(nT_д).

В отношении селекции цифровых сигналов по частоте, как это понимается применительно к реле, в РИО которых ведётся аналоговая фильтрация сигналов с целью выделения сигнала промышленной частоты, цифровым фильтром называют частотно-избирательную систему, обрабатывающую только цифровые сигналы. К таким фильтрам относятся фильтры низких частот (ФНЧ), высоких частот (ФВЧ), полосно-пропускающие (ППФ) и полосно-заграждающие (ПЗФ).

Как любая цифровая система, цифровой фильтр реализуется аппаратными, программными или аппаратно-программнымисредствами. Первый способ подразумевает использование элементов различного функциональных назначения: логических схем, триггеров, регистров, сумматоров, умножителей, ячеек памяти и т. п. Второй — языков программирования высокого уровня либо ассемблеров. Аппаратно-программная реализация цифрового фильтра представляет собой комбинацию первых двух способов: какая-то часть функция выполняется аппаратно, а остальная часть — программно.

В цифровых системах ввод аналоговых сигналов производятся путём их дискретизации в равноотстоящие моменты времени, когда вместо сигнала x(t) используется дискретный сигнал x_д(t)х(пТ_д), фиксируемый в цифровом виде с заданными уровнями квантования с определённой точностью. Для последующего использования цифровых сигналов обычно требуется их дополнительная обработка, позволяющая выделить содержащуюся в них необходимую информацию. В частности, как и в аналоговых устройствах, возникает необходимость выделения среднего или действующего значения сигнала по его выборкам, интегрирования и т. д.Для выполнения этих функций производятся операции с цифровыми последовательностями х(пТ_д), превращающие их в другие последовательности у(пТ_д), обладающие требуемыми свойствами.

Цифровые фильтры относятся к линейным дискретным системам (ЛДС), осуществляющим однозначное преобразование входной цифровой последовательности х(пТ_д) в выходную у(пТ_д).

В общем случае цифровой фильтр описывается разностным уравнением с вещественными коэффициентами

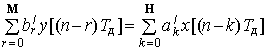,                                                                   (1.1)

где a^/_k,b^/_k — коэффициенты разностного уравнения; M, N — число отсчётов реакции и выборок воздействия, учитываемых при цифровой обработке.

Решая уравнение (1.1) относительно текущего отсчёта у(пТ_д), имеем реакцию цифрового фильтра

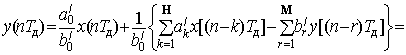
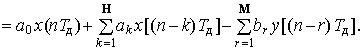                                            (1.2)

Уравнение (1.2) определяет алгоритм производимых микропроцессором вычислений, в котором используются как выборки входного сигнала x(пТ_д), так и предшествующие отсчёты реакции у(пТ_д), поэтому имеет рекурсивный характер и соответствует так называемому рекурсивному цифровому фильтру.

Рассмотрим передаточную функцию в виде суммы простых дробей 1-й степени ():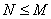

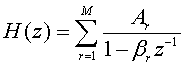                                                                                        (1.3)

Где 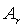- коэффициент разложения при r-м полюсе (константа), являющийся числом того же типа, что и полюс  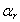(полюсы  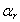в общем случае могут быть комплексно-сопряженными);

Возьмём 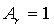 и 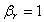, тогда передаточная функция примет вид:

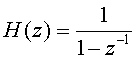                                                                                                     (1.4)

Найдём нули и полюса функции и запишем соответствующее разностное уравнение.

Для отыскания двух нулей и двух полюсов приведём заданную дробно-рациональную функцию к виду с положительными значениями степеней при переменной z:

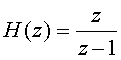                                                                                                         (1.5)

Нули функции H(z) — корни приведенного квадратного уравнения, образованного из её числителя: z. Решение этого уравнения даёт одно значение корня:

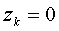
Полюса функции H(z) — корни приведенного квадратного уравнения, образованного из её знаменателя: z-1. Решение второго уравнения так же одно значение корня:

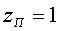
Теперь запишем разностное уравнение, соответствующее передаточной функции:

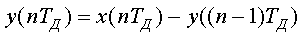                                                           (1.6)

На основании этого уравнения построим временные зависимости реакции ЛДС на различные виды воздействия.

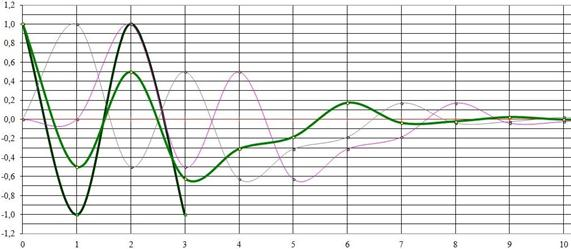
Рис. 1. Реакция ЛДС на дискретное воздействие в виде двух единичных импульсов

Рассмотрим реакцию рекурсивной ЛДС с передаточной функцией в виде суммы простых дробей 1-й степени на апериодическое воздействие при разных выборках. Эти фильтры работают с 3 и 24 гармониками. Все гармоники имеют сдвиг по фазе 0.

Фильтр работает согласно разностному уравнению:

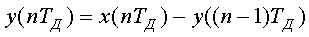                                                          (1.7)

При 6 выборках за период значительно подавляется 3 гармоника. Однако, если брать 12 выборок за период заметно подавление не только 3, но и 7 гармоники. При 24 выборках за период цифровой фильтр подавляет 15 и 9 гармоники.

Данный цифровой фильтр можно использовать в релейной защите, а именно в защите от однофазных замыканий на землю (ЗОЗЗ)

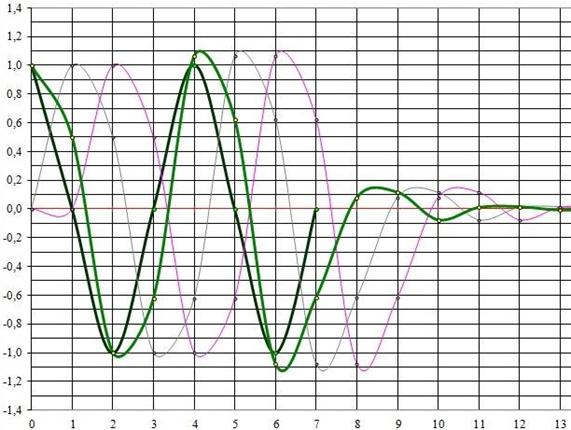
Рис. 2. Реакция ЛДС на дискретное воздействие в виде апериодической единичной косинусоиды, дискретизированной четырьмя отсчетами

Литература:

1.                  Никитин А. А. Электронные реле: Учеб. пособие. Чебоксары: Изд-во Чуваш. ун-та, 2005. 204 с.

2.                  Никитин А. А. Микропроцессорные реле: Учеб. пособие. Чебоксары: Изд-во Чуваш. ун-та, 2006. 448 с.

3.                  Федосеев А. М. Релейная защита электроэнергетических систем. Релейная защита сетей: Учеб. пособие для вузов. — М.: Энергоатомиздат, 1984. — 520 с.