Статистика отказов шин легковых автомобилей

Автомобиль представляет собой сложную систему состоящей из множества элементов. Каждый из элементов вносит свой вклад в надежность всей системы. Одним из таких элементов являются автомобильные шины. И хотя процесс замены неисправного элемента на исправный не представляет больших трудностей автомобиль выходит из строя. Следовательно, происходит снижение показателей надежности транспортного средства. При отдельном рассмотрении автомобильных шин к ним применимы все свойства надежности: безотказность, долговечность, ремонтопригодность, сохраняемость. В большинстве случаев надежность шин оценивают по совокупности показателей. Показателями, определяющими надежность шины, могут быть износ протектора (до минимально допустимой величины протектора), пробои и порезы, усталостные дефекты каркаса или все показатели сразу. Так в [1] представлены функции вероятности безотказной работы грузовых шин по перечисленным показателям. Примеры распределения партии восстановленных шин снятых с эксплуатации по пробегу и определение ожидаемого пробега шин представлены в [2].

На основании статистических данных по обращениям в шиномонтажную мастерскую проведен анализ надежности автомобильных шин. В качестве показателей надежности предлагается использовать вероятность безотказной работы шин, вероятность отказов, частота отказов, интенсивность отказов, гамма-процентный ресурс шин, закон распределения выхода шин из строя по пробегу. Такие свойства надежности как ремонтопригодность и сохраняемость автомобильных шин в данной работе не рассматривались. При сборе информации о ресурсе шин фиксировался факт снятия шин с эксплуатации и ремонтные операции в статистических данных не отражались. В соответствии с нормативной документацией завод-изготовитель автомобильных шин гарантирует ее сохраняемость в течении 5 лет с даты изготовления.

По исходным данным было проведено распределение шин по пробегу со следующими параметрами: количество интервалов разбиения m = 15; длина интервалов Δt = 11334 км. В результате получена гистограмма частот распределения отказов шин по пробегу (рис. 1).

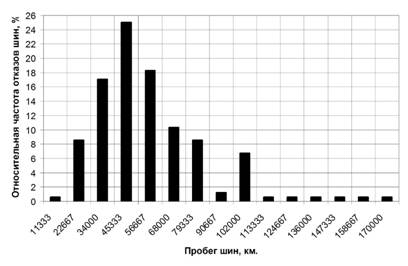
Рис. 1. Гистограмма частот распределения отказов шин по пробегу

В соответствии с [3] вероятностью безотказной работы называется количественная мера того, что при определенных условиях эксплуатации в заданном интервале времени или в пределах заданной наработки не произойдет ни одного отказа и определяется по формуле:

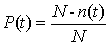                                                                                                            (1)

где: N — число испытываемых объектов; n(t) — число отказавших элементов за время t

Вероятностью отказа называется количественная мера того, что при определенных условиях эксплуатации в заданном интервале времени возникает хотя бы один отказ. Отказ и безотказная работа являются событиями несовместными и противоположными. Следовательно, вероятностью отказа определяется по формуле [3]:

Q(t) = 1 — P(t)                                                                                                              (2)

Расчетные значения по формулам (1) и (2) представлены в виде графиков на рис. 2. По графику можно определить гамма-процентный ресурс шин. Он определяется как суммарная наработка, в течение которой объект не достигнет предельного состояния с вероятностью гамма, выраженной в процентах [4]. Тогда 90 % гамма-процентный ресурс составит 23000 км пробега, что соответствует вероятности безотказной работы шин равной 0,9. кроме того из анализа интегральных функций (рис. 2) видно, что 50 % вероятность безотказной работы шин составляет 45000 километров пробега. Частотой отказов по статистическим данным называется отношение числа отказавших элементов в единицу времени к первоначальному числу работающих (испытываемых) и определяется по формуле [3]:

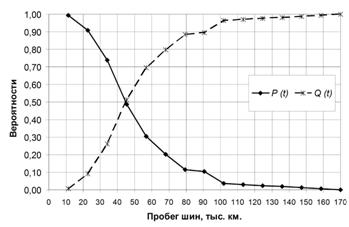
Рис. 2. Интегральные функции безотказной работы P(t) и отказов Q(t)

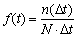                                                                                                                     (3)

где: n(Δt) — число отказавших элементов в интервале времени от (t — Δt)/2 до (t + Δt)/2

Интенсивностью отказов по статистическим данным называется отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени [3].

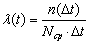                                                                                                                  (4)

где: N_ср — среднее число исправно работающих изделий в интервале Δt

Величины частоты и интенсивности отказов имеют одинаковый порядок значений и размерность, поэтому могут изображаться в одних координатах. Результаты расчетов по формулам (3) и (4) представлены на рис. 3.

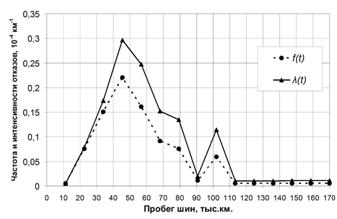
Рис. 3. График зависимости частоты f(t) и интенсивности l(t) отказов шин от пробега

Среднее время (пробег) безотказной работы вычисляется по формуле [3]:

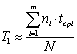                                                                                                                     (5)

где: t_срi находится по следующей формуле: t_срi=(t_i-1+ t_i)/2

где: t_i–1 — время начала i-го интервала; t_i — время конца i-го интервала

В результате расчетов по формуле (5) получаем, что средний пробег безотказной работы шин составлякт T₁ = 50790 км.

В общем случае результаты наблюдений выхода шин из строя (рис. 1) могут подчиняться некоторому теоретическому закону распределения. Проверку соответствия теоретического распределения проводится с помощью критерия соответствия c². Выбранное теоретическое распределение подтверждается, если выполняется условие [5]:

c² < c²_a                                                                                                                          (6)

где: c² — расчетное значение параметра; c²_a — теоретическое значение параметра

Для 10 %-ного уровня значимости и числа степеней свободы равном 6, табличное значение c²_a = 10,645 [5]. При подборке теоретических распределений получены следующие результаты:

1. Нормальное распределение — c² = 39,16

2. Гамма распределение — c² = 14,97

3. Логарифмически нормальное распределение — c² = 9,26

Условие (6) выполняется только для логарифмически нормального распределения:

9,26<10,645

Следовательно, при определении надежности шин принимается логарифмически нормальный закон распределения. На рис. 4 представлены кривые теоретического распределения и экспериментальных данных.

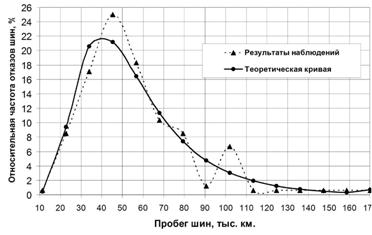
Рис. 4. Теоретическое распределение и экспериментальные данные отказов шин

Соответствие экспериментальных данных логарифмически нормальному закону распределения означает, что случайная величина (пробег шины) зависит от большого числа независимых факторов [6]. Действительно, на надежность автомобильных шин влияют многие факторы: качество шин, состояние дороги, скорость автомобиля, мастерство водителя, давление в шинах, углы установки колес и другие.

На основании представленных данных можно сделать следующие выводы. Статистические данные по пробегу шин легковых автомобилей соответствуют логарифмически нормальному закону распределения. В соответствии с гистограммой (рис. 1) наибольшее количество шин, примерно 42 %, выходят из строя при пробеге 45–56 тысяч километров. А по теоретическому закону максимум выходов из строя шин (41,5 %) приходится на пробег 34–45 тысяч километров (рис. 4). В тоже время средний пробег безотказной работы составляет 50790 километров. Наибольший пробег шин доходит 170000 километров. До пробега более 90000 километров «доживают» лишь 12 % шин и вероятность их отказа составляет 0,9. Однако это показывает, что имеется возможность увеличения надежности автомобильных шин в эксплуатации за счет повышения качества факторов, определяющих их ресурс.

Литература:

1.       Третьяков О. Б. Автомобильные шины. Конструкция, механика, свойства, эксплуатация / О. Б. Третьяков, В. А. Гудков, А. А. Вольнов, В. Н. Тарновский. — М.: КолосС, Химия, 2007. — 432 с.

2.       Евзович В. Е. Восстановление изношенных пневматических шин / В. Е. Евзович — М.: Автополис-плюс, 2005. — 624 с.

3.       Корчагин А. Б. Надежность технических систем и техногенный риск: учебное пособие в двух частях. Часть 2. Практикум / А. Б. Корчагин, В. С. Сердюк, А. И. Бокарев. — Омск: Издательство ОмГТУ, 2011. — 140 с.

4.       Курчаткин, В.В Надежность и ремонт машин / В. В. Курчаткин, Н. Ф. Тельнов, К. А. Ачкасов и др.; под ред. В. В. Курчаткина. — М.: Колос, 2000. — 776 с.

5.       Львовский Е. Н. Статистические методы построения эмпирических формул / Е. Н. Львовский. Учебное пособие для втузов. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1988. — 239 с.

6.       Айвазян С. А. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное издание / С. А. Айвазян, И. С. Енюков, Л. Д. Мешалкин. — М.: Финансы и статистика, 1983. — 471 с.