Алгоритм получения матрицы жесткости четырехугольного конечного элемента

В статье исследуются в трех вариантах алгоритмы получения матриц жесткости четырехугольного конечного элемента.

Ключевые слова: объемный конечный элемент, матрица жесткости, вектор узловых неизвестных.

Для расчета осесимметрично нагруженных тел вращения из несжимаемых материалов разработаны объемные конечные элементы с поперечным сечением в виде четырехугольника. Для выполнения численного интегрирования произвольный четырехугольник в системе координат r, z с узлами i, j, k, l отображался на квадрат с локальными координатами ξ, η, изменяющимися в пределах -1 ≤ ξ, η ≤ 1. Зависимость между координатами r, z и локальными координатами ξ, η определялась билинейными соотношениями

; ,                                                                         (1)

где  — матрицы-строки координат узлов четырехугольника.

Дифференцированием соотношений (1) определялись производные глобальных координат r,_ξ, r,_η, z,_ξ, z,_η и локальных координат ξ,_r, η,_r, ξ,_z, η,_z в глобальной системе координат.

Четырехугольный конечный элемент разрабатывался в трех вариантах.

1. Столбец узловых неизвестных содержит только перемещения и принимается в виде

;                                                           (2)

где

 — перемещения вдоль осей r и z соответственно в узловой точке m (m = i, j, k, Каждая составляющая перемещения внутренней точки конечного элемента аппроксимируется через узловые неизвестные билинейными зависимостями (1).

Вектор-столбец внутренней точки конечного элемента  определяется в матричном виде выражением

,                                                                                                            (3)

где матрица [A] имеет вид

.

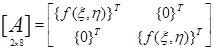Деформации внутренней точки конечного элемента определяются матричным выражением

.                                                                      (4)

Гидростатическое давление σ₀ принимается постоянным по площади четырехугольника.

2. Во втором варианте конечного элемента в каждом его узле в качестве узловых неизвестных принимаются перемещения и их первые производные. Вектор узловых неизвестных в локальной системе координат имеет вид

,                                                                                               (5)

где

;

;

 — производные радиального и осевого перемещений в локальной системе координат.

Перемещения внутренней точки конечного элемента определяются через векторы узловых перемещений в локальной системе координат соотношениями

;,                                                                     (6)

где компонентами матрицы , содержащей функции формы, являются полиномы Эрмита третьей степени.

С использованием аппроксимирующих соотношений (6) формируется матричная зависимость (3) и (4).

Гидростатическое давление принимается постоянным по площади четырехугольника.

3. В третьем варианте конечного элемента перемещения аппроксимировались соотношениями второго варианта, а гидростатическое давление считалось изменяющимся в зависимости от узловых значений по билинейному закону

,                                                                                                   (7)

где

.

Для получения матрицы жесткости и векторов узловых усилий дискретных элементов при действии сил, распределенных по объему, используется равенство работ внешних и внутренних сил на возможных перемещениях

v,                                                                                        (8)

где

 — элементарный объем дискретного элемента;

 — вектор-строка составляющих поверхности сил.

С использованием матричной зависимости

,                                                           (9)

равенство (8) принимает вид

,                                                                          (10)

где

ds — элементарная площадка поперечного сечения элемента.

Объемная деформация ε₀, входящая в (15), определяется выражением

.                                                      (11)

Принимая во внимание (3), (4), (9), (10) и (11) выражение (12) представим в виде

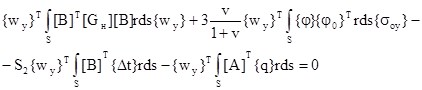                             (13)

Выполняя минимизацию функционала (13) по компонентам вектора  и по компонентам узловых неизвестных гидростатического давления , получим систему уравнений

;

,                                                                                                                 (14)

где

;

;

.

Систему (14) можно представить в традиционной конечно-элементной формулировке

,                                                                                                         (15)

где

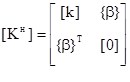 — модифицированная матрица жесткости конечного элемента;

 — вектор узловых сил конечного элемента.

 — вектор узловых неизвестных конечного элемента.

При получении матриц жесткости в первом и втором вариантах конечных элементов матрица [β] соотношения (14) представляет собой столбец {β}.

Модифицированная матрица жесткости [К^н] имеет размеры 9×9 — в первом варианте конечного элемента, 25×25 — во втором варианте и 28×28 — в третьем варианте.

В качестве примера определено напряженно-деформированное состояние защемленной по торцам цилиндрической оболочки, нагруженной внутренним давление интенсивности q=, при следующих исходных данных: внутренний радиус R=0,5 м; толщина стенки оболочки h=0,05 м; модуль упругости материала Е = 2 · 10^5; коэффициент Пуассона υ = 0,5. расчет выполнялся в трех вариантах.

В первом варианте использовался конечный элемент с узловыми неизвестными в виде радиального и осевого перемещения υ. Гидростатическое давление σ₀ принималось постоянным по площади четырехугольника.

Во втором варианте расчет выполнен с использованием конечного элемента, узловыми неизвестными которого являлись перемещения и их первые производные. Гидростатическое давление σ₀ принималось постоянным по площади сечения объемного конечного элемента.

В третьем варианте расчета использовался элемент с узловыми неизвестными в виде перемещений и их первых производных. Гидростатическое давление распределялось в поперечном сечении объемного конечного элемента по линейному закону.

Анализ результатов показал хорошую сходимость вычислительного процесса и совпадение результатов по вариантам.

Сравнительными расчетами установлено, что наилучшие результаты получаются при использовании конечного элемента с узловыми неизвестными в виде перемещений и их первых производных, а также гидростатических давлений (т. е. в третьем варианте).