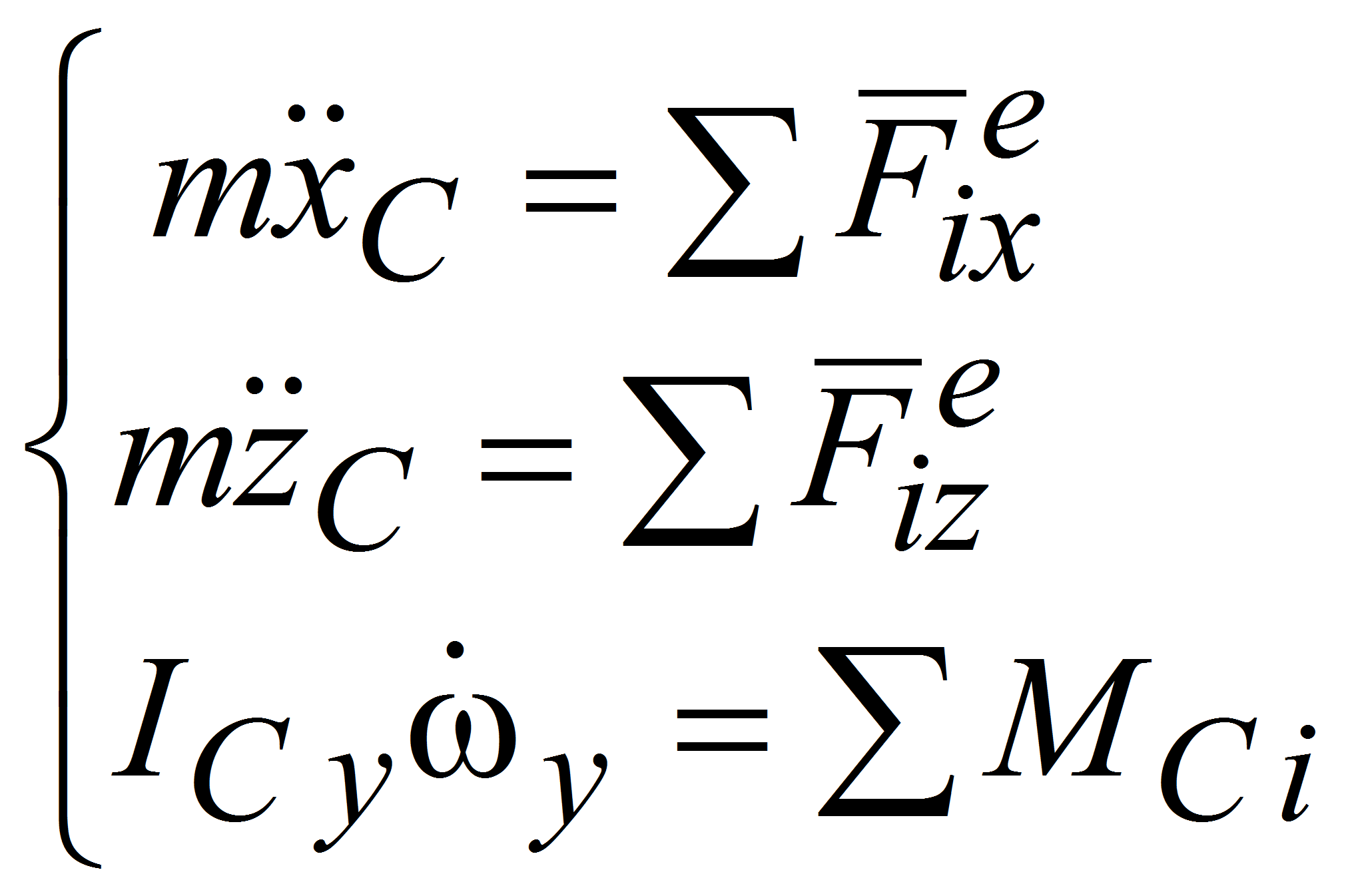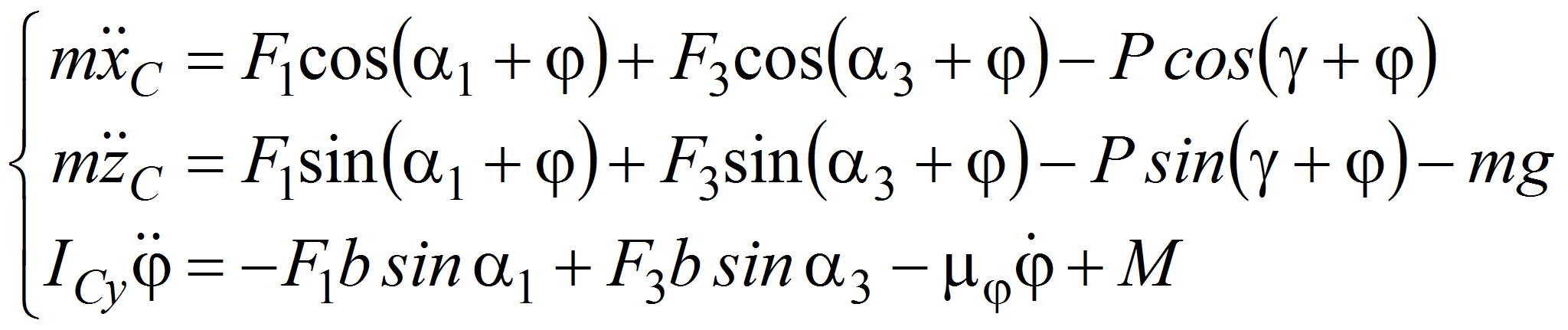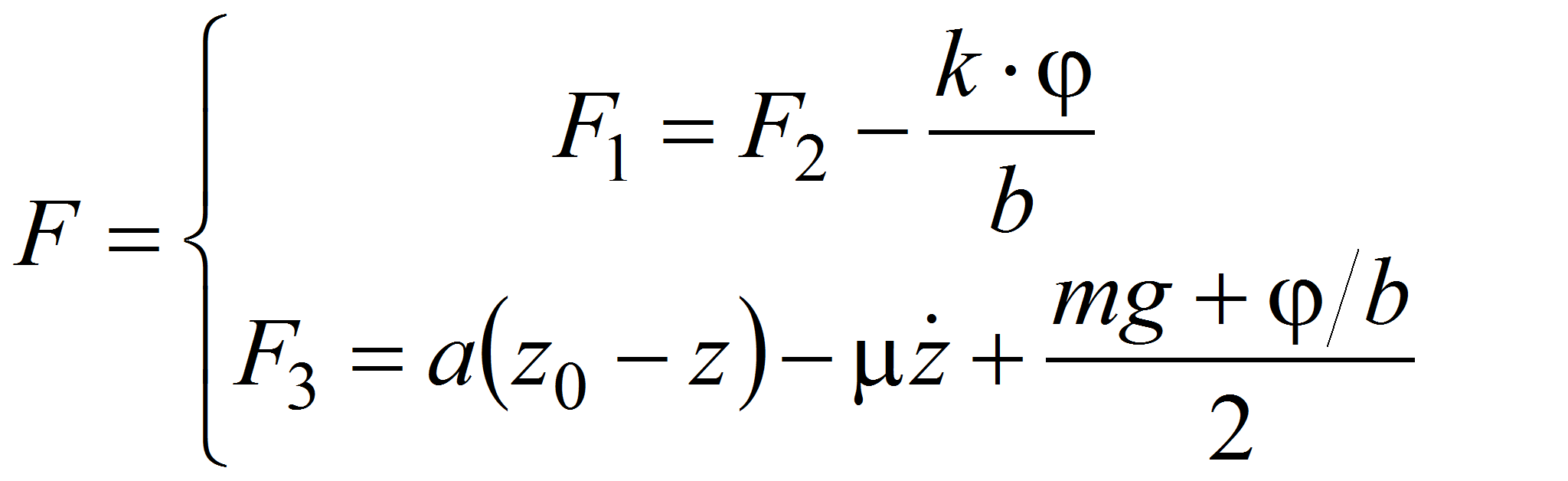Введение
В последние годы началось развитие нового класса небольших беспилотных квадрокоптеров, способных нести полезную нагрузку в виде контролирующих приборов, видеоаппаратуры. Квадрокоптеры, в отличие от беспилотных летательных аппаратов (БЛА) вертолетного типа традиционной продольной схемы с несущим и рулевым винтами и аппаратов соосной схемы, обладают рядом достоинств, таких, как простота и надежность конструкции. Вопросам расчета параметров квадрокоптера и систем управления уделено большое внимание в работах [1–6]. Такие устройства характеризуются малой взлетной массой компактностью и высокой маневренностью. Центральная часть квадрокоптера — «фюзеляж» служит для размещения оборудования, нагрузки и аккумуляторов. Радиально от центра на балках устанавливаются микроэлектродвигатели с несущими винтами, образуя звездообразную компоновку всего аппарата. Такая симметричная компоновка, предполагает наличие передней и задней частей, относительно которых сориентировано направление движения.
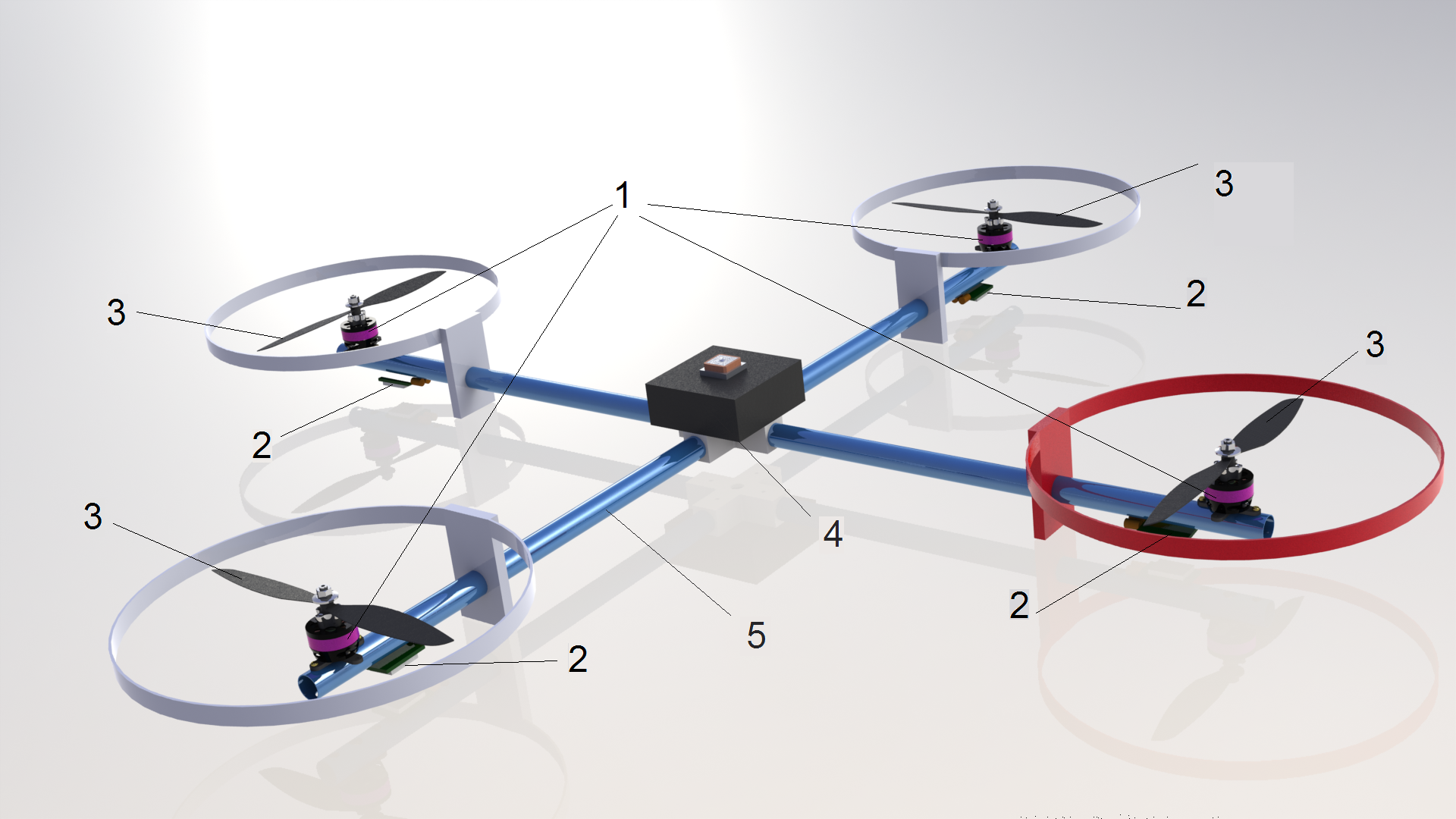
Общий вид квадрокоптера показан на рис.1.
Рис. 1. Общий вид квадрокоптера: 1 — бесколлекторные двигатели; 2- регуляторы оборотов; 3- винты 10х45 разнонаправленного вращения; 4- центральная плата управления; 5-фюзеляж (корпус)
Математическая
модель квадрокоптера
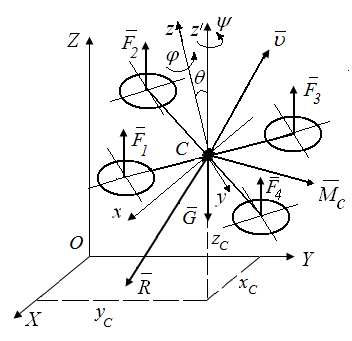
- Для изучения основных закономерностей движения квадрокоптера рассмотрим математическую модель, описывающую пространственное движение летающего робота. Квадрокоптер- это электромеханическая система корпус которой можно моделировать твердым телом с 6-ю степенями свободы. Будем рассматривать движение корпуса робота в декартовой системе координат, связанной с землей Oxyz, тогда положение центра масс аппарата определяют координаты x, y, z, а ориентацию в пространстве задают углы Эйлера , , (рис. 2).
Рис. 2. Пространственная расчетная схема квадрокоптера
-
- Каждый из двигателей создает силу тяги Fi (i= 1,2,3,4), величина которой регулируется изменением уровня напряжения на двигателях. В рассматриваемой конструкции векторы Fi имеют соответствующие проекции(Fix,Fiy,Fiz) на систему координат связанную с корпусом. Правильная ориентация векторов Fi открывает широкие возможности для компенсации внешней ветровой нагрузки действующей на корпус робота.
Моделирование управляемого движения квадрокопрера в вертикальной плоскости
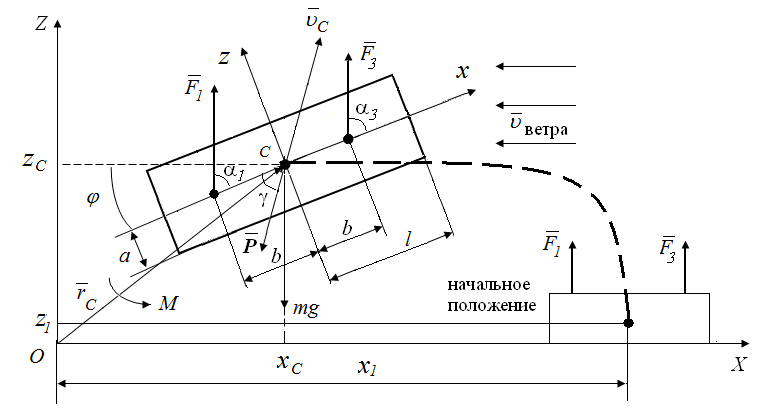
Схема движения квадрокоптера в вертикальной плоскости приведена на рис.3. Управление движением осуществляется изменением величин двух сил Fi, i=1, 2, а также углами наклона этих векторов к локальной системе координат. Ветровая нагрузка моделируется с помощью приведенной силы P(t) и момента М(t), параметры которых в общем случае изменяются по случайному закону. В данном примере представлены в виде:
где P0 и М0 — амплитуды ветровой нагрузки, P, M — частоты ветровой нагрузки, — сдвиг фазы между моментом и силой.
Рис.3. Плоская расчетная схема квадрокоптера
Введем две системы координат: абсолютную неподвижную систему координат OXZ и относительную систему координат Oxz, которая жестко связана с корпусом робота так, что начало координат O совпадает с центром масс корпуса, ось Ox параллельна траекториям движения корпуса робота.
Угол определяет поворот системы координат Oxz относительно OXZ.
Управляемыми
параметрами являются координаты xС
и zC
центра масс
корпуса устройства, угол φ
поворота
корпуса робота относительно его центра масс. В общем случае
управляющими
величинами являются силы
![]() ,
углы 1,
3,
изменяя которые можно получить любую траекторию движения.
,
углы 1,
3,
изменяя которые можно получить любую траекторию движения.
Определим радиус-вектор центра масс корпуса устройства:
Вектор скорости центра масс равен:
Со стороны окружающей среды на корпус робота действует сила моделирующая ветровую нагрузку P, определяемая по формуле:
где
![]() ,
,
![]() -
проекции силы сопротивления на оси x,
z соответственно.
-
проекции силы сопротивления на оси x,
z соответственно.
Запишем систему дифференциальный уравнений, описываемых движение объекта в вертикальной плоскости:
После соответствующих преобразований система (6) примет следующий вид:
где
![]() —
момент сопротивления вращению корпуса квадрокотера.
—
момент сопротивления вращению корпуса квадрокотера.
Пусть
в начальный момент времени летающий робот имеет нулевую
скорость:
![]() ,
а координаты центра масс заданы:
,
а координаты центра масс заданы:
![]() .
.
В дальнейшем рассмотрим случай взлета робота на заданную высоту и дальнейшее его движение вдоль оси, параллельной оси Oy по заданной траектории. При этом должно выполняться следующее условие:
z0-z 0<z< z0+z 0, x0-x 0<x< x0+x 0 а угол : -0+0<< 0+0.
Величина
z0,
x0 —
предельные величины отклонения летающего робота от заданной
траектории, определяет погрешность (![]() ),(
),(![]() )
реальной траектории движения. При превышении которой включается
управление в виде сил.
)
реальной траектории движения. При превышении которой включается
управление в виде сил.
Траектория движения летающего робота формируется в виде периодических циклов движения, описываемых функциями с малым числом изменяемых параметров. Это позволяет проводить её формирование и оптимизацию с использованием математической модели, описываемой системой нелинейных дифференциальных уравнений (7).
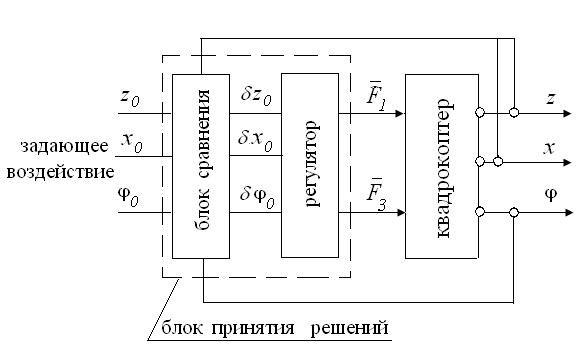
Структурная схема трехканальной системы управления движением представлена на рисунке 4.
Рис. 4. Структурная схема управления движением летающего робота
Логический регулятор системы автоматического управления (САУ) реализует управляющие воздействия по следующему алгоритму:
где![]() -
управляющие воздействия, определяются блоком принятия решений; a,
b,
k,
—
параметры
квадрокоптера.
-
управляющие воздействия, определяются блоком принятия решений; a,
b,
k,
—
параметры
квадрокоптера.
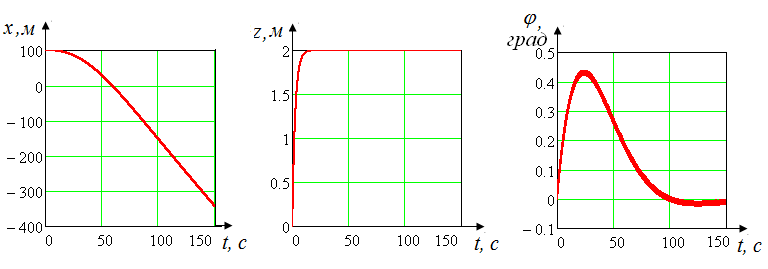
Далее проводилось численное моделирование движения квадрокопрера в вертикальной плоскости, пример которого представлен на рис.5.
Рис. 5. Графики проекции перемещений и угла поворота квадрокоптера от времени
Выводы:
В результате
математического моделирования удалось получить параметры САУ,
обеспечивающие движение центра масс и ориентацию квадрокоптера
в зависимости от углов поворота 1,
3,
управляющих параметров![]() и
и
![]() .
Так при 1=3=900
(рис.5) наблюдается движение квадрокоптера в зоне отрицательных
значений осей Ox,
связанное
с инерционными составляющими,
стабильное
поддержание заданной высоты (ось Oz),
а также незначительный разворот корпуса квадрокоптера
и дальнейшее его выравивание.
.
Так при 1=3=900
(рис.5) наблюдается движение квадрокоптера в зоне отрицательных
значений осей Ox,
связанное
с инерционными составляющими,
стабильное
поддержание заданной высоты (ось Oz),
а также незначительный разворот корпуса квадрокоптера
и дальнейшее его выравивание.
Литература:
- Т.Bresciani. Modeling, identification and control of a quadrotor helicopter. Master’s thesis, Department of Automatic control, Lund University, October 2008,170p.
- Carlo Alberto Pascucci. Design, Construction and Model Predictive Control of a Quadrocopter Autonomous Aerial Vehicle, September 2010. p. 30–33.
- A. Bemporad, C. A. Pascucci, and C. Rocchi. Hierarchical and hybrid model predictive control of quadcopter air vehicles. In 3rd IFAC Conference on Analysis and Design of Hybrid Systems, Zaragoza, Spain, 2009, p.14–19.
- G. V. Raffo, M. G. Ortega, and F. R. Rubio. An integral predictive/nonlinear
control structure for a quadrotor helicopter. Automatica46 (2010)p.29–39.
- Bouabdallah, S., Murrieri, P., & Siegwart, R. Design and control of an indoor micro quadrotor. In Proc. IEEE Int. conf. on rob. and automat., Vol. 5, New Orleans, USA (pp. 4393_4398),(2004).
- Castillo, P., Lozano, R., & Dzul, A. Stabilization of a mini rotorcraft with four rotors. IEEE Control Systems Magazine(2005a), 45–55.