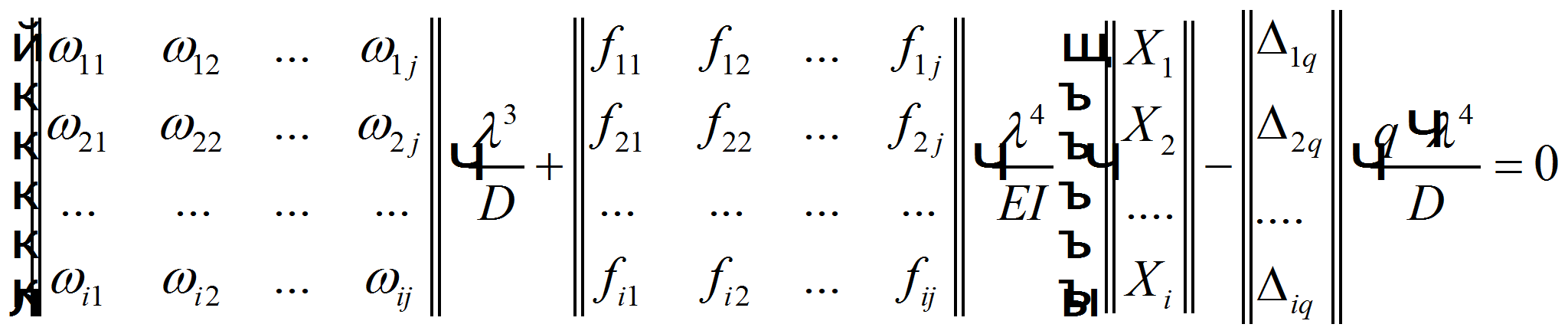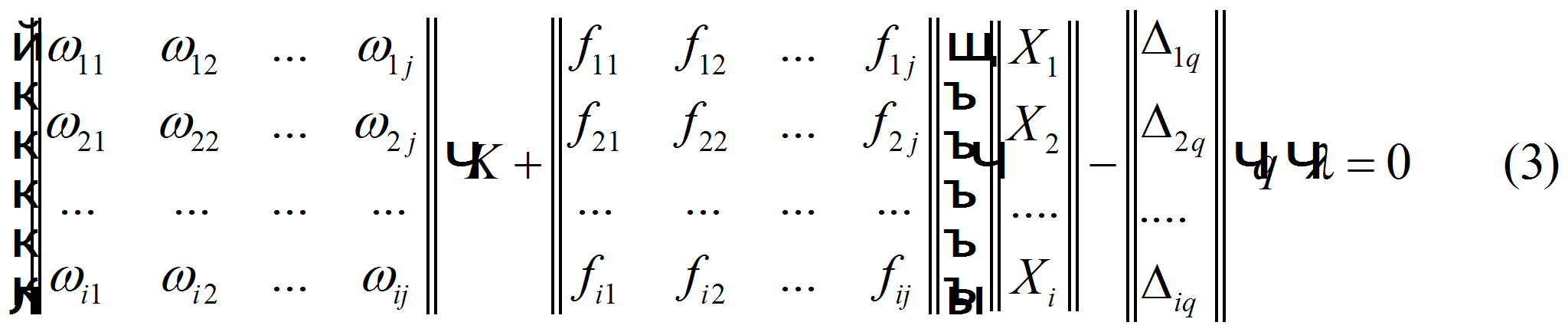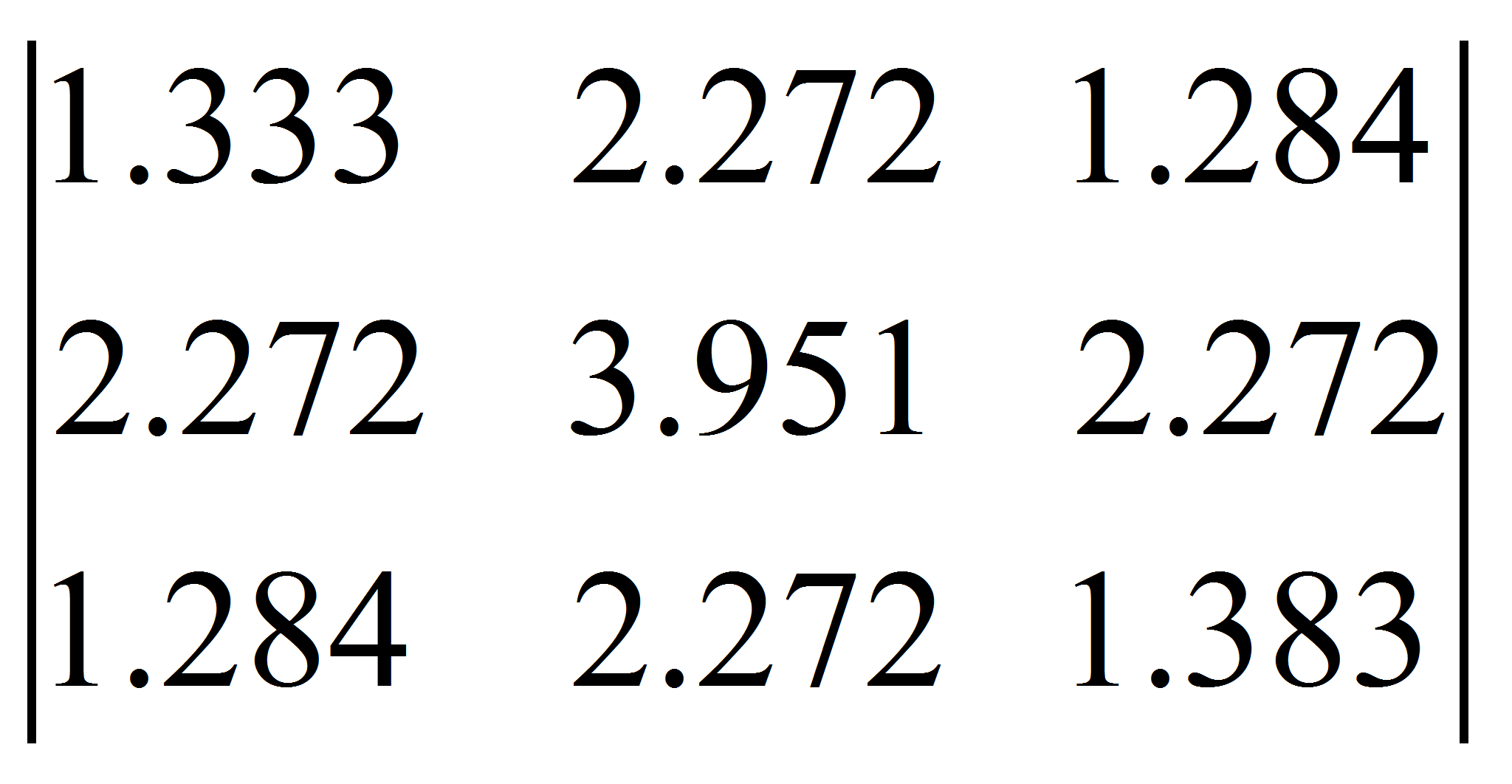Современные вычислительные комплексы позволяют решить на ЭВМ широчайший круг задач прочности и жесткости, как конструкции в целом, так и ее элементов.

В данной работе предлагается яркий пример сочетания «неограниченных» возможностей ЭВМ с классическим методом сил строительной механики, позволяющий исследовать деформированное состояние комбинированной системы.

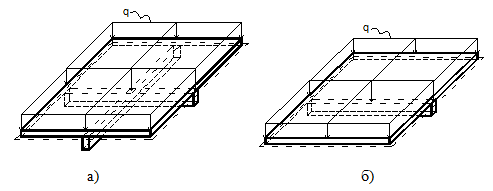
Рассматривается загруженная равномерно распределенной нагрузкой прямоугольная пластина, шарнирно опертая по четырем сторонам, которая также подкрепляется одной и более балками (рис. 1). Внедрение в работу пластины системы балок позволит снизить прогибы системы, уменьшить размеры сечения плиты, и соответственно снизить расход материала.

Рис. 1. Схемы подкрепления плиты. а — подкрепляется системой балок; б — подкрепляется одной балкой;

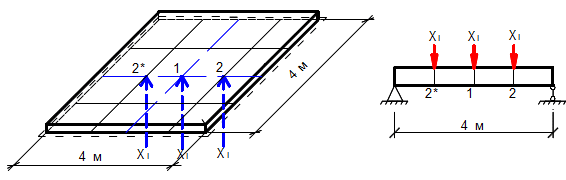
Расчет ведется в три этапа. Первый этап предполагает расчет системы (рис. 2.), состоящей из прямоугольной пластины с постоянными по всей площади жесткостью и сечением, и балки, также имеющей постоянные по длине жесткость и сечение.

Размеры пластины: длина a=4 м; ширина b=4 м; толщина 200 мм; размеры балки: высота сечения h=400 мм; ширина сечения d=200 мм; длина l=4 м.

Рис. 2. К расчету конструкции 1-го этапа.

Для ведения расчета и обеспечения точек контакта элементов системы пластина условно разбивается на квадратные ячейки с размером стороны равным 1 м, балка разбивается на участки длиной 1 м.

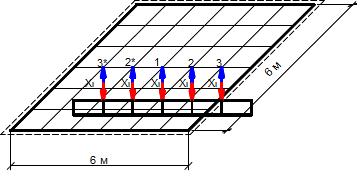
Второй этап предполагает расчет квадратной пластины с длиной стороны 6 м, подкрепленной балкой длиной 6 метров (рис. 3.) с жесткостными характеристиками аналогичными предыдущему типу балки. Разбиение пластины и балок на участки соответствует разбиению на первом этапе.

Рис. 3. Схема взаимодействия балки и пластины в задаче 2-го этапа.

Вид снизу.

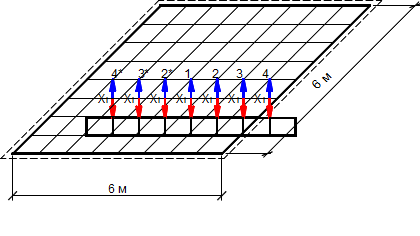
Третий этап предполагает уточнение решения предыдущей задачи, и представляет собой расчет системы (рис. 4), состоящей из аналогичной прямоугольной пластины толщиной 200мм, но имеющей ячейки разбивки размером 0,75х0,75м и 0,75м для пластины и балки соответственно. Жесткость пластины, а также жесткость и размеры сечения балки аналогичны типам балок и пластины на первом и втором этапах.

Рис. 4. Схема взаимодействия балки и пластины в задаче 3-го этапа.

Вид снизу.

Основная расчетная схема (рис. 2.) этой конструкции получена разделением ее на две части: пластина, балка. Реальный континуальный контакт этих структур заменяется ограниченным числом связей, воспринимающих только вертикальные усилия, которые принимаются за «лишние» неизвестные , где — число симметрично расположенных связей. Совместность прогибов пластины и балок в местах установленных связей представляется уравнениями метода сил в матричной форме:

где — суммарная матрица коэффициентов при лишних неизвестных- вектор прогибов пластины от заданного вектора нагрузки,- матрицы коэффициентов при лишних неизвестных, - расстояние между выбранными точками по линии контакта элементов;D — изгибная жесткость пластины; E — модуль упругости материала балки, I–момент инерции сечения балки.

С помощью данной зависимости мы в дальнейшем определим прогибы от совместной работы пластины и балок, перейдем к матричной форме определения моментов в характерных сечениях плиты и балок, и, в конце концов, сможем составить алгоритм подбора оптимального сечения и жесткости подкрепляющих балок в рамках данного исследования. Все математические операции выполнены в среде Mathcad. Подтверждение результатов и графическое дополнение данного исследования выполнено на конечно-элементных моделях в среде программного комплекса (ПК) «Лира».

На первом этапе была выполнена постановка задачи, а именно произведен расчет отдельных частей системы: пластины и балки. Пластина была смоделирована в ПК «Лира» из прямоугольных конечных элементов (КЭ) № 41 с размером стороны 50 мм. Балка моделировалась с помощью стержневых КЭ № 10 длиной 50 мм.

В первую очередь был произведен расчет в ПК «Лира» по определению прогибов пластины без балок, нагруженной равномерно распределенной нагрузкой , откуда получены грузовые прогибы пластины . За счет дискретизации системы и упрощения расчета, рассматриваемые точки контакта плиты и балки были выбраны на расстоянии 1 м по линии контакта элементов конструкции. Далее в этих точках соответственно для пластины и балки прикладываются неизвестные силы взаимодействия элементов , которые для их определения заменяются единичными силами, что позволяет нам определить единичные прогибы в этих точках. Таким образом, сумма полученных величин войдет в - матрицу коэффициентов при лишних неизвестных, а величины войдут в матрицу грузовых перемещений и уравнение (1) примет вид:

(2).

Для дальнейших операций с жесткостью элементов, введем в систему коэффициент , предварительно умножив все слагаемые уравнения на множитель . В итоге получим уравнение (2) в следующем виде:

Как видно из уравнения (3) матрицы, при большом количестве рассматриваемых точек могут приобретать большие размеры. В силу того, что прогибы будут одинаковыми в точках симметричных относительно осей симметрии пластины, при условии ее центрального опирания на балку или систему балок, данные кососимметричные матрицы можно упростить.

Для упрощения математических операций, т. е. уменьшения размеров матриц и для наглядности работы системы авторами был разработан алгоритм (табл. 1.) составления коэффициентов для матриц, позволяющий вести расчет по данному методу не только прямоугольных, но и любых других пластин, имеющих в плане одну и более осей симметрии.

Таблица 1

_ij=n f_ij

(_ij =nw_ij)

….

_ik=n f_ik

(_ik =nw_ik)

_ji=n f_ji

(_ii=nw_ji)

_jj=n(f_jj+ f_jj^*)

(_jj =n(w_jj+w_jj^*))

….

_jk=n(2f_jk)

(_jk =n(2w_jk))

….

….

….

….

_ki=n f_ki

(_ii=nw_ki)

_kj=n(2f_kj)

(_kj=n(2w_ki))

….

_kk=n(f_kk+ f_kk^*)

(_kk =n(w_kk+w_kk^*)

Примечание к таблице: n — «число симметрии», т. е. число, равное количеству симметрично-одинаковых точек. Главные коэффициенты матриц соответствуют прогибам в точках симметричной половины линий контакта элементов. Побочные коэффициенты — сумма прогибов в симметричных точках, умноженная на «число симметрии». Цветом выделены коэффициенты для составления матрицы ; для матрицы используется аналогичный алгоритм.

Пример применения данного алгоритма вычисления коэффициентов для матриц при 5-ти неизвестных силах взаимодействия в точках контакта, согласно задаче второго(рис. 2). этапа приведен ниже:

L₁=>>через алгоритм>>L_1*=

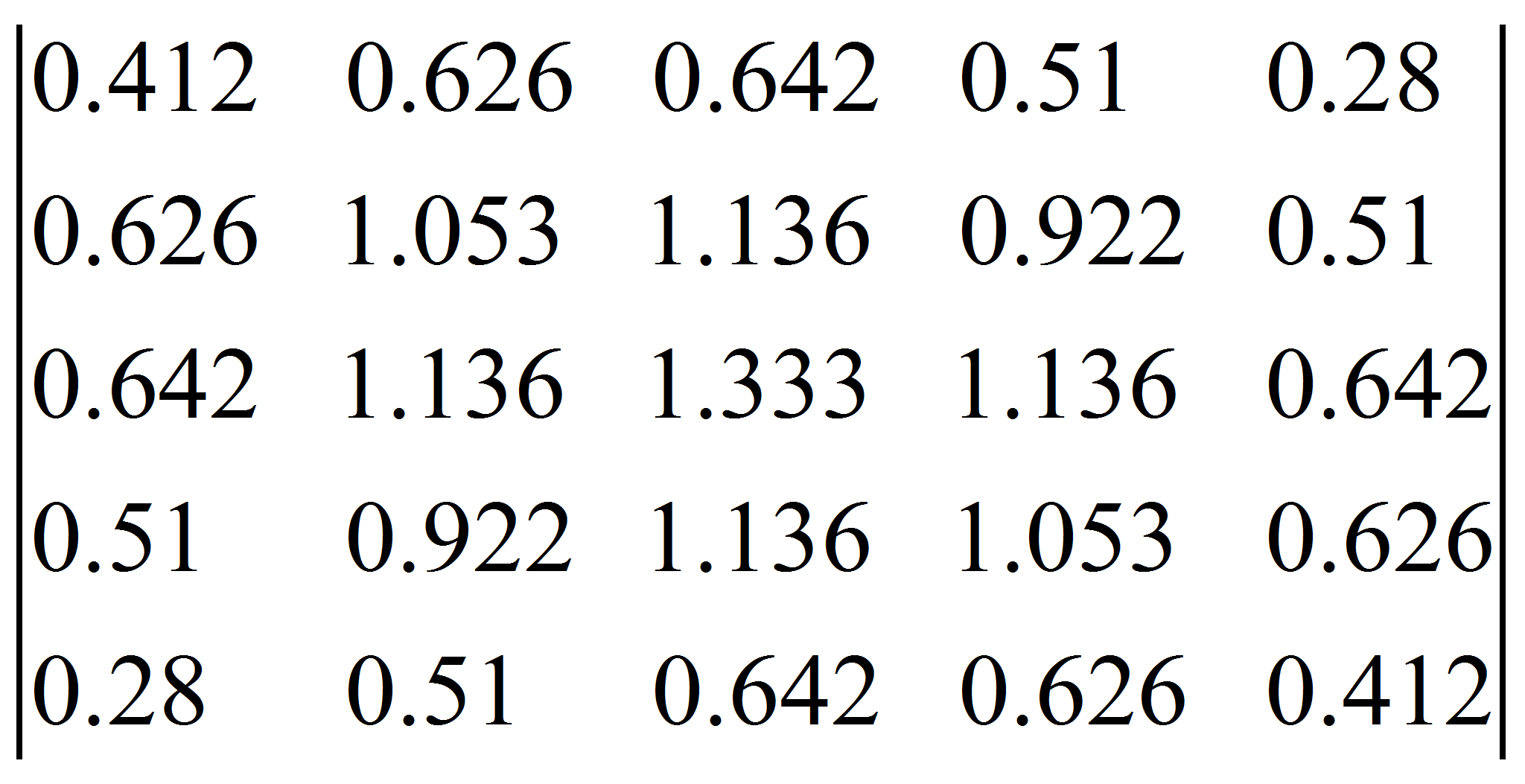
Как видно по примеру исходная квадратная матрица была сведена к матрице, и во всех других случаях, исходная квадратная матрица по данному алгоритму будет сведена к матрице , что существенно облегчает расчет, и, позволяет более точно осуществлять визуальный контроль правильности заполнения матриц.

Внедрение в ход работы расчета задачи 2-го этапа позволило нам проследить закономерность изменения размеров матриц с применением данного алгоритма.

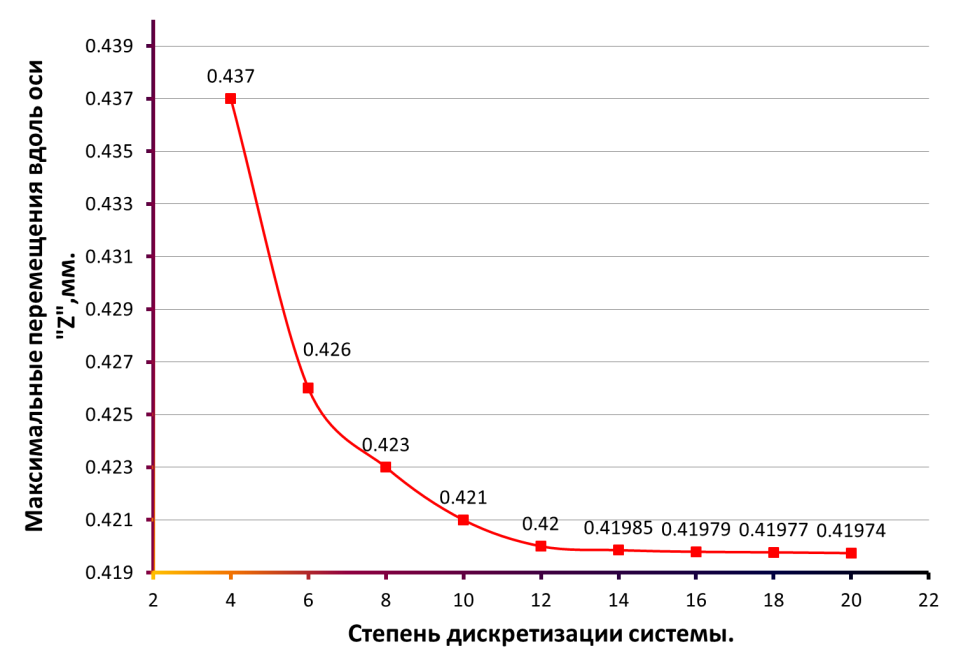
На третьем этапе, как говорилось ранее, было произведено уточнение результатов расчета задачи второго этапа, а именно установлена зависимость значения максимальных прогибов конструкции от степени дискретизации системы, т. е. произведено увеличение количества, и соответственно размеров ячеек разбивки элементов (размеры ячеек: 0,75х0,75м для пластины и 0,75м для балки) для задачи второго этапа и проведен перерасчет. Данная зависимость для квадратной пластины представлена на графике (рис. 5).

Рис. 5. Зависимость максимальных прогибов (вертикальных перемещений) конструкции от степени дискретизации системы.

Примечание к рисунку: степень дискретизации для данной задачи представлена количеством ячеек пластины в ряду; число ячеек балки соответствует числу ячеек в ряду пластины. Масштаб осей различный. Ось «Z» вертикальная глобальная ось при расчете конструкции.

После решения данных задач был проведен анализ системы задачи третьего этапа и определена зависимость прогибов от изменения коэффициента «К», введенного ранее, а именно от изменения размеров поперечного сечения балки.

Как видно из графика, значение максимального прогиба в зависимости от степени дискретизации уменьшается по экспоненциальному закону, и при ее увеличении значение прогиба начинает стремиться к конечному максимальному его значению, тем самым отражая приближение работы элементов системы к работе континуальной, с бесконечно большим числом степеней свободы системы. Данная зависимость для квадратной пластины представлена на графике (рис. 6).

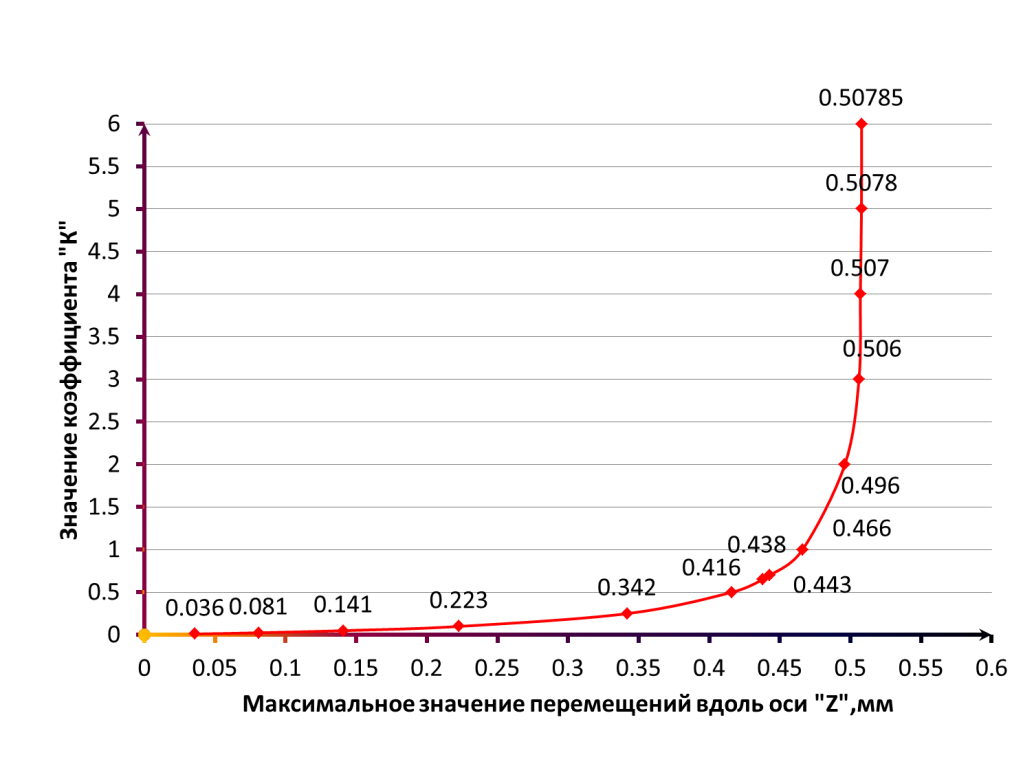
Рис. 6. Зависимость максимальных прогибов (вертикальных перемещений) конструкции от коэффициента «К».

Примечание к рисунку:

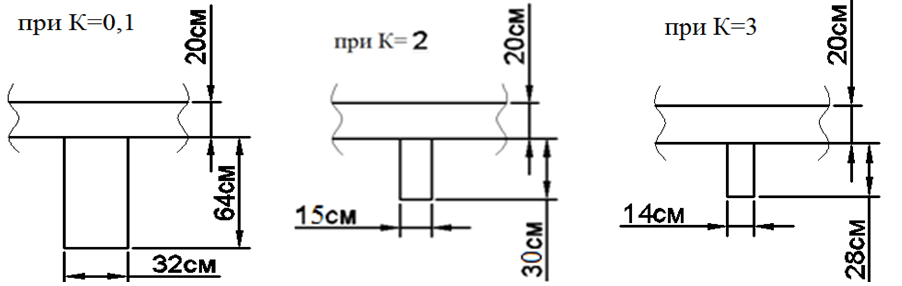
Рис. 7. Размеры сечения балки при различных значениях коэффициента «К».

По графику видно, что при увеличении коэффициента «К», т. е. при уменьшении сечения балки, происходит увеличение максимального прогиба конструкции по экспоненциальному закону. А на участке кривой между значениями прогиба 0,5 мм и 0,55 мм кривая начинает стремиться к значению конечного прогиба конструкции, при котором сечения балки не будет хватать для снижения прогибов системы. Тем самым балка постепенно начнет выключаться из работы до ее полного разрушения.

Что касаемо системы перекрестных балок, которая подкрепляет пластину, то алгоритм исследования деформированного состояния всей конструкции аналогичен предыдущим операциям. Отличие лишь в том, что расчет и поиск неизвестных сил взаимодействия ведется по двум перпендикулярным линиям контакта элементов, а именно добавляются соответствующие коэффициенты для матриц уравнения (2).

Для определения моментов в характерных сечениях, соответствующих расположению точек контакта элементов, воспользуемся матричной формой записи уравнения метода сил для моментного усилия в элементе:

Операции нахождения значений моментов по ранее полученным значениям сил взаимодействия соответствуют матричным операциям предыдущих расчетов. Таким образом, получив значения сил взаимодействия и произведя вычисления по формуле (4) мы найдем значения изгибающих моментов действующих на балку и пластину в нужных нам сечениях, что в дальнейшем позволит произвести расчет прочности данных элементов. Зависимости значений изгибающих моментов от степени дискретизации и коэффициента «К» аналогичны зависимостям прогибов от этих величин.

В итоге данной работы было исследовано деформированное состояние пластины подкрепляемой балкой или системой перекрестных балок, а именно установлены зависимости изменения прогибов и моментов от степени дискретизации системы, от коэффициента «К». Варьируя коэффициентом, выражающим соотношение этих жесткостей, можно подобрать оптимальные геометрические характеристики элементов, тем самым обеспечить прочность и жесткость конструкции. Для выполнения данного подбора в среде программирования Mathcad был составлен элементарный программный код, позволяющий подбирать оптимальные сечения элементов, учитывая нужные нам начальные параметры и условия работы данной конструкции.

Литература:

1. Ильин В. П., Карпов В. В., Масленников А. М. Численные методы решения задач строительной механики. 1990. Минск. 349 с.
2. Суворов А. А. Дискретный метод сил. Статический расчет пластины, подкрепленной перекрестными балками [Текст] / А. А. Суворов// Студенческая наука. Исследование в области архитектуры, строительства и охраны окружающей среды. Тезисы докладов 31-й межвузовской студенческой научно-технической конференции по итогам НИР студентов в 2011 году. — Самара, 2012. — с.105.