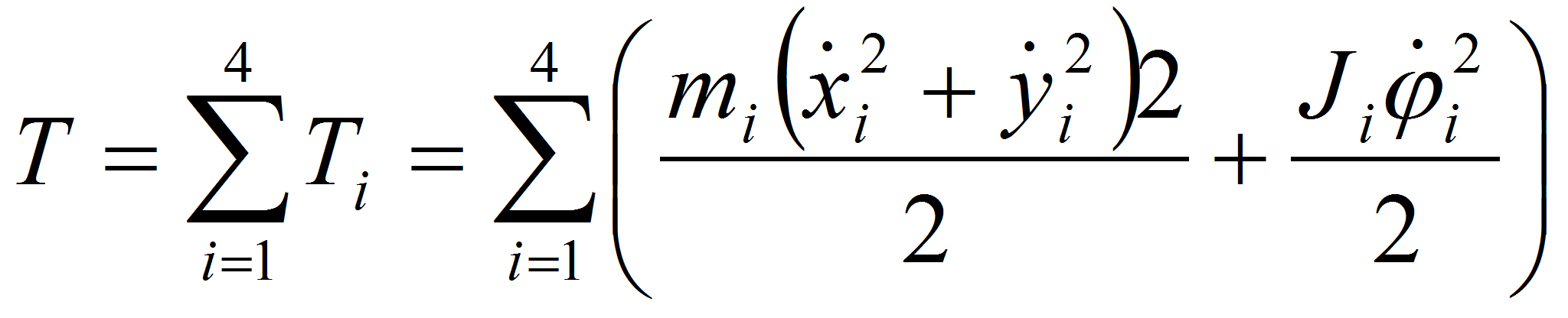Введение
Среди большого многообразия конструкций прыгающих роботов широкое распространение получили устройства, использующие ногу в качестве модуля, посредством которого осуществляется отрыв от поверхности [1–3]. Целью работы является разработка математической модели объекта, относящегося к описанному виду прыгающих роботов, и системы управления высотой и длиной прыжка за счет вариации параметров разгона.
Математическая модель прыгающего робота
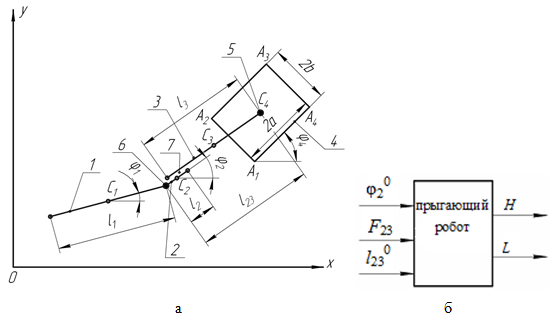
Прыгающий робот представляет собой четырехзвенную систему, конструктивно состоящую из стопы — звено 1, ноги — звенья 2 и 3, корпуса — звено 4 (рис. 1, а).
Рис. 1. а — расчетная схема четырехзвенного прыгающего робота, б — система управления высотой и длиной прыжка.
Приводы вращательного движения 5 и 6 соединяют звенья 4 и 3, 2 и 1, привод линейного перемещения 7 связывает звенья 2 и 3. В вертикальной плоскости Оху звенья 1, 2 и 3 представляют собой стержни длинами l1, l2 и l3, а звено 4 имеет вид прямоугольника с размерами 2ax2b. Массы звеньев сосредоточены в центрах их симметрии — точках Сi, i=1–4. Будем рассматривать случай, когда звено 3 установлено в точке С4. Углы наклона звеньев робота к положительному направлению оси Ох равны φ1, φ2 и φ4, в связи с тем, что звенья 2 и 3 не могут поворачиваться друг относительно друга, то углы наклона этих звеньев к оси Ох равны. Расстояние l23 относительного перемещения звеньев 2 и 3 является переменной величиной и может варьироваться в диапазоне от l23min, когда звенья ноги и стопы полностью втянуты в корпус, до l230, при котором происходит отрыв звена 1 робота от поверхности.
Положение звеньев устройства описывается вектором координат
в котором q1=х1, q2=y1, q3=х4, q4=у4 — координаты центров масс звеньев 1 и 4 в системе Оху, q5=φ1, q6=φ2 и q7=φ4 — углы поворота звеньев, q8=l23 — длина ноги робота.
Для записи системы дифференциальных уравнений движения робота используются уравнения Лагранжа второго рода, в которых кинетическая энергия системы определяется по формуле:
где
![]() ,
,
![]() —
центральные моменты инерции звеньев,
—
центральные моменты инерции звеньев,
![]() ,
,
![]() —
проекции скоростей центров масс звеньев на оси Ох и Оу.
—
проекции скоростей центров масс звеньев на оси Ох и Оу.
Прыжок робота состоит из последовательности этапов, во время каждого из которых звенья робота совершают определенные виды движения [4]. В матричном виде система дифференциальных уравнений движения объекта имеет вид:
где
![]() ,
,
![]() ,
,
![]() —
матрицы коэффициентов,
—
матрицы коэффициентов,
![]() —
матрица обобщенных сил, определяемые на каждом этапе прыжка
в отдельности.
—
матрица обобщенных сил, определяемые на каждом этапе прыжка
в отдельности.
В соответствии с предложенной последовательностью этапов движения прыгающего робота на геометрические размеры его звеньев наложены следующие ограничения:
l23min+l1≤b,
l23min+
l1≤a,
l2≤b,
l2≤a,
l3≤b,
l3≤a,
![]() ,
,
где φ20 — угол наклона звена 2, при котором происходит разгон робота до его отрыва от поверхности.
Система управления параметрами полета
В работе предлагается система управления высотой и длиной прыжка устройства, в которой в качестве управляющих параметров выступают: φ20 — угол наклона ноги, под которым осуществляется разгон робота, F23 — модуль силы, разгоняющей робота, l230 –длина ноги робота, на которой происходит разгон (рис. 1, б). Высота и длина прыжка представляют собой расстояния вдоль осей Ох и Оу соответственно с момента отрыва звена 1 от поверхности до достижения наибольших значений вдоль указанных осей.
Моделирование прыжка устройства
Для осуществления моделирования движения устройства численным способом полученная математическая модель реализации одного прыжка была преобразована к безразмерному виду, масштабные коэффициенты равны М=0.05 кг, Т=0.1 с, L=0.1 м. В качестве объекта моделирования рассматривается прыгающий робот, масса корпуса которого намного больше масс звеньев ноги и стопы: m1=1, m2=1, m3=1, m4=7. Геометрические размеры робота с учетом ограничений равны: а=1, b=1, l1=0.5, l2=0.9, l3=0.9, l23min=0.4, l230=1.8. Будем рассматривать три варианта втягивания звеньев 1–3 ноги и стопы в корпус робота во время его полета:
- нога не втягивается в корпус,
- нога полностью втягивается в корпус со скоростью v,
- нога полностью втягивается в корпус под действием силы F.
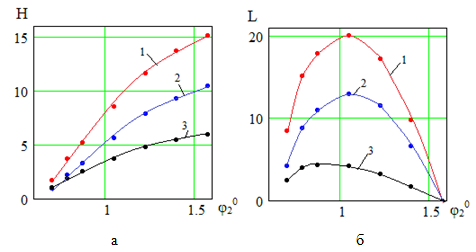
На рис. 3 приведены графики высоты и длины прыжка от угла наклона ноги при разгоне робота под действием постоянной силы F23=160. По рис. 3, а видно, что высота прыжка возрастает по криволинейному закону с увеличением угла φ20. Длина прыжка также увеличивается по некоторой кривой до достижения углом наклона ноги значения φ20=π/3 при равномерном втягивании ноги в корпус в полете или в случае, когда нога не втягивается (кривые 1 и 2 соответственно), и φ20=5π/18 при втягивании ноги под действием силы F, а затем убывает. При φ20=π/2 длина прыжка равна 0, робот совершает вертикальный прыжок.
Рис. 3. Зависимости: а — H(φ20), б — L(φ20); 1 — нога не втягивается; 2 — нога втягивается со скоростью v=5; 3 — нога втягивается под действием силы F=5.
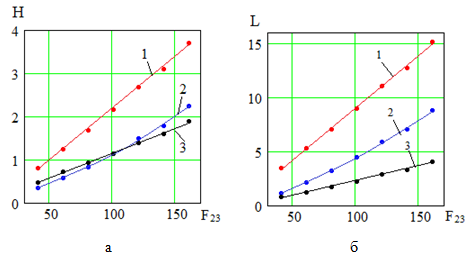
Рис. 4. Зависимости: а — H(F23), б — L(F23) при φ20=π/4; 1 — нога не втягивается; 2 — нога втягивается со скоростью v=5; 3 — нога втягивается под действием силы F=5.
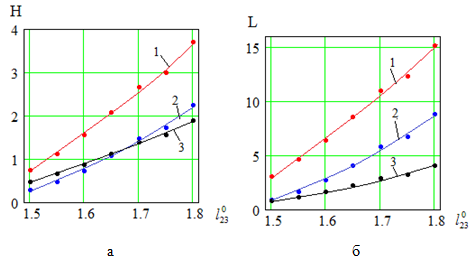
Рис. 5. Зависимости: а — H(l230), б — L(l230) при φ20=π/4; 1 — нога не втягивается; 2 — нога втягивается со скоростью v=5; 3 — нога втягивается под действием силы F=5.
По графикам рис. 4 установлено, что высота и длина прыжка робота возрастают пропорционально значению силы F23, разгоняющей устройство для совершения прыжка, независимо от способа втягивания ноги в полете.
При увеличении длины полностью выдвинутой ноги, на которой происходит разгон робота до его отрыва от поверхности, наблюдается возрастание высоты и длины прыжка практически пропорционально расстоянию l230 (рис. 5).
Заключение
В работе описана математическая модель прыгающего робота, представляющего собой четырехзвенную систему, состоящую из корпуса, ноги, образованной двумя звеньями, и стопы. Разработана система управления высотой и длиной прыжка устройства, в которой в качестве управляющих величин выступают параметры разгона робота. По результатам математического моделирования установлены закономерности между управляемыми и управляющими параметрами для случаев равномерного и равноускоренного втягивания ноги в полете и при отсутствии втягивания ноги. Полученные зависимости могут использоваться при проектировании прыгающих роботов, использующих ногу в качестве модуля, за счет осуществляется отрыв от поверхности.
Литература:
- Cherouvim E. P. N. Energy saving passive-dynamic gait for a one-legged hopping robot // Robotica. 2006. Vol. 24. No. 4. P. 491–498.
- Ahmadi M., M. Buehler“Stable control of a simulated one-legged running robot with hip and leg compliance // IEEE Transactions on Robotics and Automation. 1997. Vol. 13. No. 1. P. 96–104.
- Carl´esi N., Chemori A. Nonlinear Model Predictive Running Control of Kangaroo Robot: a One-Leg Planar Underactuated Hopping Robot // The 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems. 2010. Р. 3634–3639.
- Волкова, Л. Ю. Исследование различных режимов движения робота, перемещающегося с отрывом от поверхности / Л. Ю. Волкова, С. Ф. Яцун // Сборник научных трудов международной молодежной конференции «Мехатроника. Современное состояние и тенденции развития». г. Орехово-Зуево, 2012. С. — 66–71.