Метод проекций яркости при поиске зрачка на изображении

Авторы: Трекин Алексей Николаевич, Матвеев Иван Алексеевич

Рубрика: 1. Информатика и кибернетика

Опубликовано в

международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2012)

Статья просмотрена: 1015 раз

Библиографическое описание:

Трекин, А. Н. Метод проекций яркости при поиске зрачка на изображении / А. Н. Трекин, И. А. Матвеев. — Текст : непосредственный // Технические науки: теория и практика : материалы I Междунар. науч. конф. (г. Чита, апрель 2012 г.). — Чита : Издательство Молодой ученый, 2012. — С. 24-28. — URL: https://moluch.ru/conf/tech/archive/7/2227/ (дата обращения: 26.04.2024).

Предлагается метод быстрого определения на изображении глаза точки, лежащей внутри зрачка, которая может далее использоваться как его приближённый центр. Используются проекции яркости бинаризованного изображения на вертикальную и горизонтальную оси. Произведена экспериментальная проверка на доступных базах изображений радужки.
Ключевые слова: сегментация изображений, распознавание радужки, проекция яркости

Введение

Идентификация личности человека по изображению радужной оболочки - один из развивающихся методов биометрии, уже имеющий применение в системах доступа. Он основан на том, что рисунок радужной оболочки глаза имеет индивидуальную, слабо меняющуюся со временем структуру. Одним из этапов распознавания радужной оболочки является выделение зрачка на изображении глаза. Это необходимо, чтобы локализовать радужную оболочку, которую затем сравнивают с эталоном.

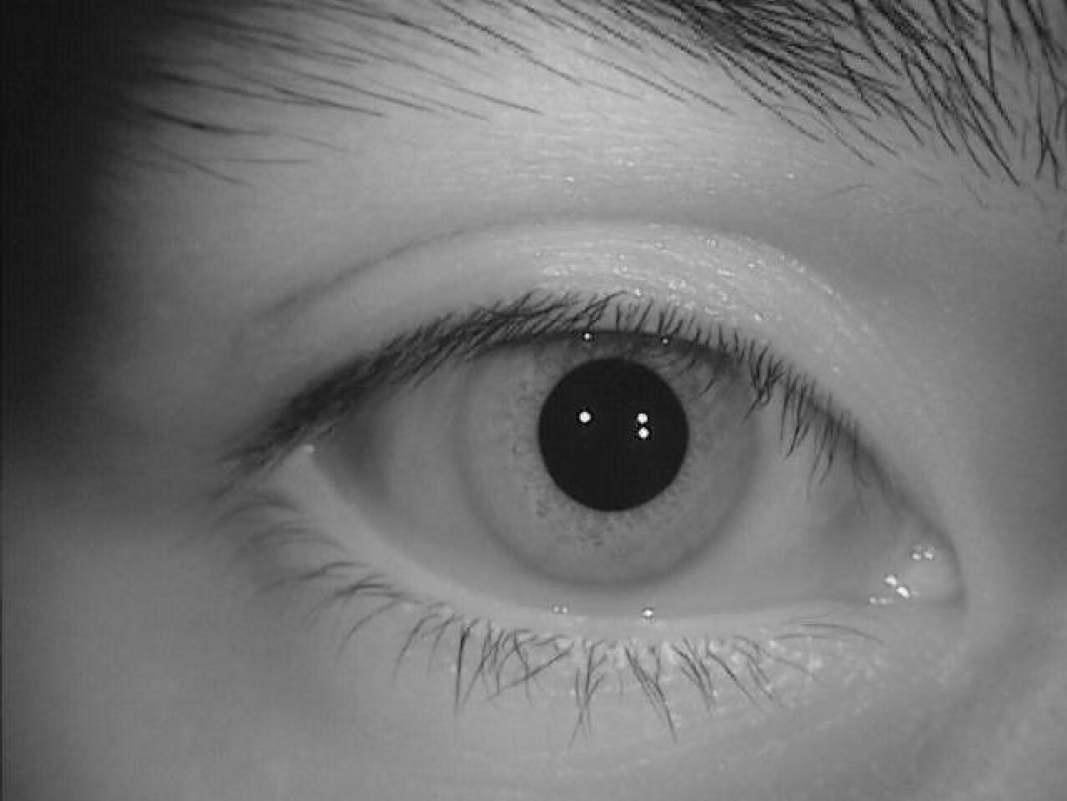
Рис 1. Исходное изображение глаза, база CASIA, 640*480, 256 градаций серого.
Зрачок большинства людей имеет форму, близкую к кругу [14], и отражает очень мало света, если направление освещения не совпадает с направлением камеры. Это позволяет искать его как тёмный круг на изображении. Наиболее часто используемым является метод Даугмана [1]. На нём основано большинство разработанных коммерческих приложений. Поиск трёх параметров положения окружности (две координаты центра и радиус) осуществляется при помощи следующего интегро-дифференциального оператора:

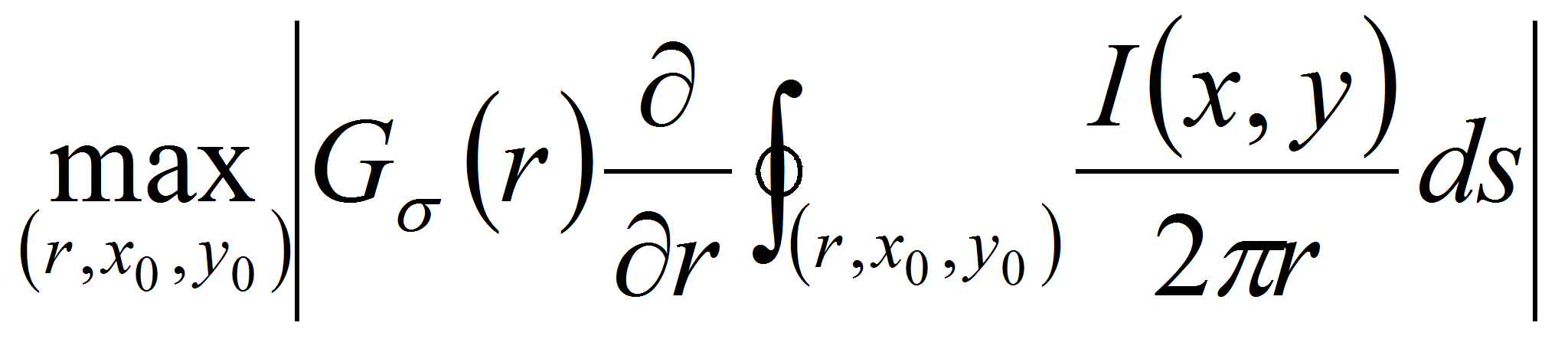
где 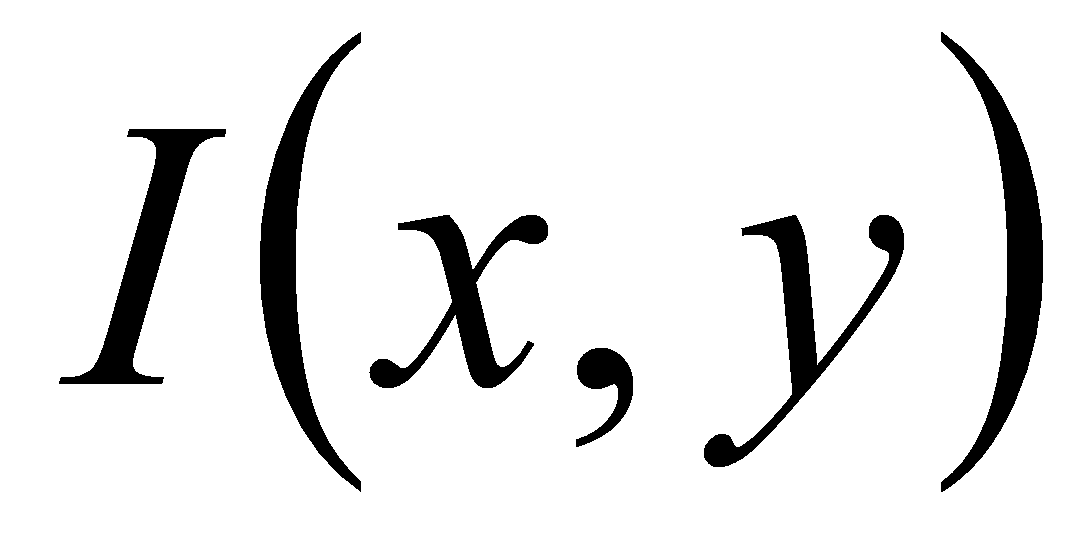– яркость изображения.
Оператор ищет область на изображении, где достигается максимум частной производной от нормализованного интеграла по 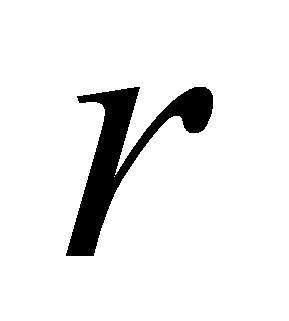по направлению увеличения величины радиуса. Многие методы основаны на работе с градиентом яркости и различными вариантами преобразования Хафа. В таких методах сначала производится градиентное преобразование изображения, то есть приближенное вычисление частных производных яркости изображения в каждой точке. Так как зрачок сильно отличается от окружающей его радужки по яркости, на его границе - окружности - значения градиента принимают большие значения. Затем необходимо найти параметры этой окружности, для чего применяют преобразование Хафа [9], позволяющее найти параметры кривых заданного типа, в данном случае - окружностей. Таковы методы, используемые в [2], [3]. В [4] для ускорения также используется предварительная бинаризация изображения.
Нашей целью было создание алгоритма, предлагающего оценку координат центра зрачка, причём основной идеей было сократить время работы программы за счёт точности определения центра, по сути, мы претендуем лишь на то, что обнаружили точку, лежащую внутри зрачка. Для ускорения работы, в основном, используется уменьшение объёма данных, с которыми работает алгоритм, а именно - переход от исследования двумерного массива 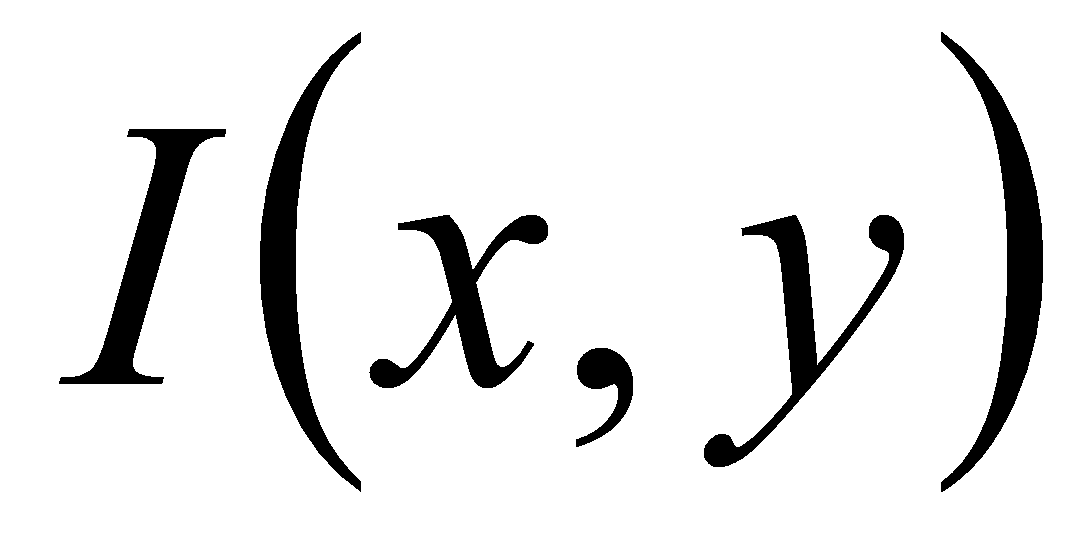изображения, к исследованию одномерных массивов - «проекций» зрачка на координатные оси. Полученный результат может быть использован для уменьшения зоны поиска зрачка другим, более точным и менее быстрым методом, что может уменьшить суммарное время. Также результат можно использовать в алгоритмах, которые ищут параметры зрачка, используя точку, лежащую не далее, чем половина радиуса от истинного центра зрачка, например [6]. В работе [7] также применяются проекции, которые строятся как сумма яркостей всех точек с данной координатой по одной из осей. Для нахождения глаза на фотографии лица человека использовался тот факт, что проекции испытывают большие изменения в районе глаз. В работе [8] используется горизонтальная проекция бинаризованного изображения для грубого определения расположения глаза.

Описание алгоритма

Алгоритм состоит из следующих шагов.

Бинаризация изображения с плавающим порогом.
Проекции на координатные оси
Поиск координат центра зрачка

Шаг 1.Бинаризация

Бинаризация — получение бинарного изображения из изображения с 256 градациями серого. В данном случае используется простая пороговая функция:

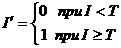
где 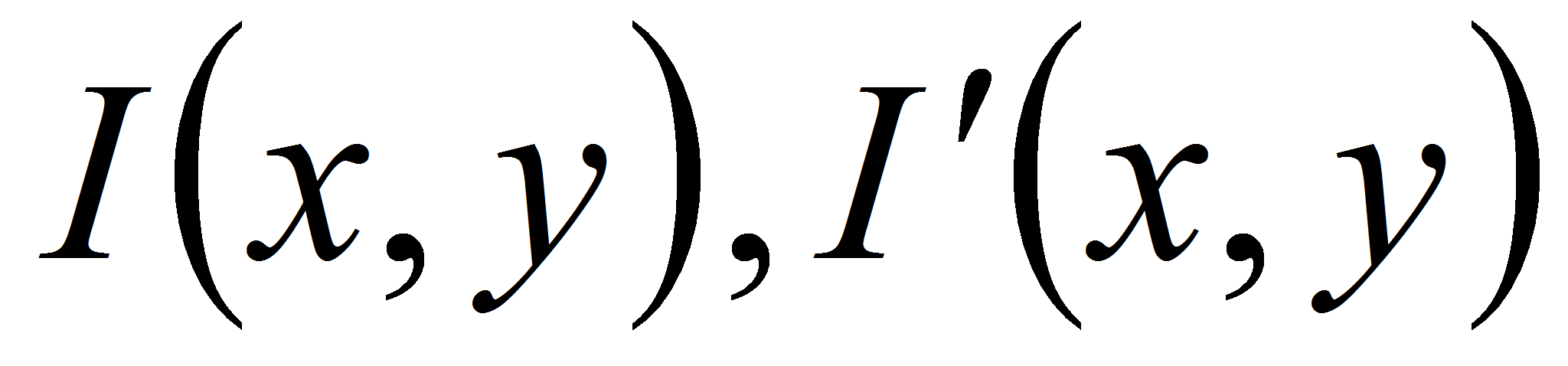- яркости точки исходного и бинаризованного изображений соответственно, - некий порог, который подбирается в с помощью исследования гистограммы изображения.Предполагается, что зрачок, как крупная по площади область с небольшой и практически равномерной яркостью, даст первый достаточно резкий и высокий максимум на гистограмме. Этот максимум ищется как первая точка, отвечающая условиям:
1) 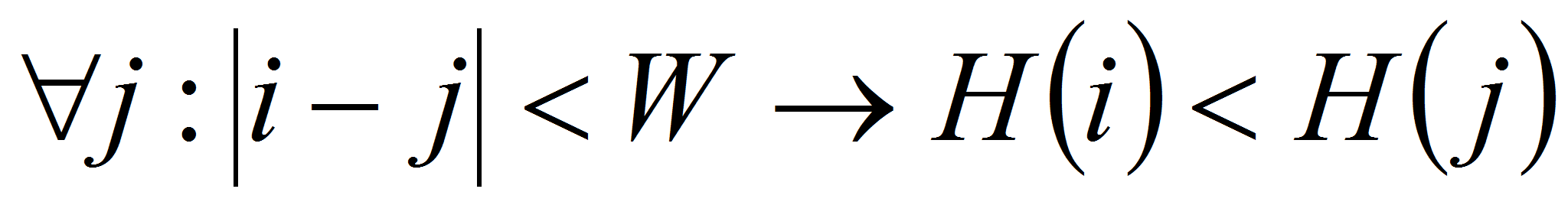- условие локального максимума,
2) 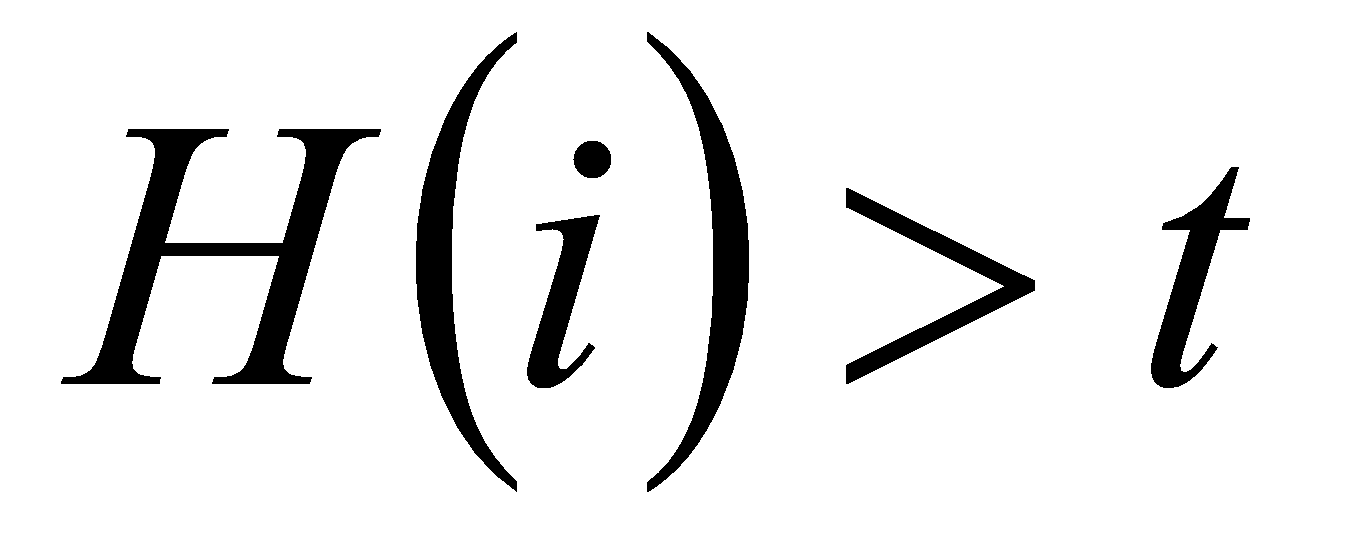- условие достаточной высоты,
3) 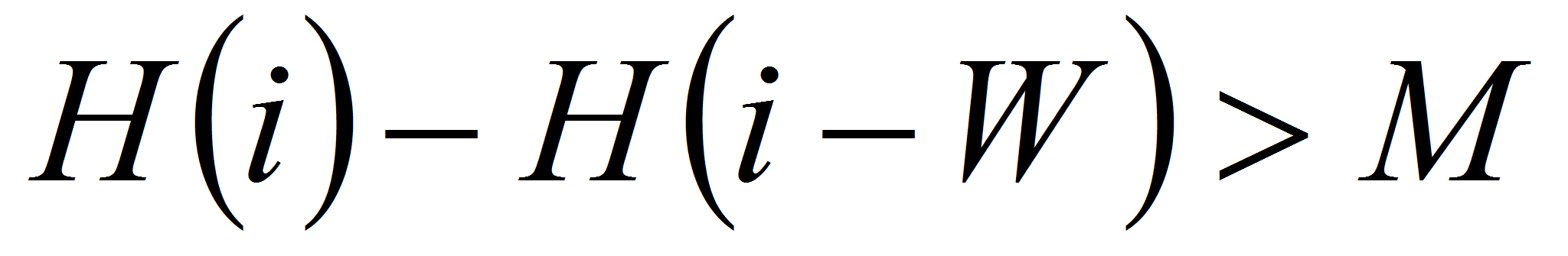; 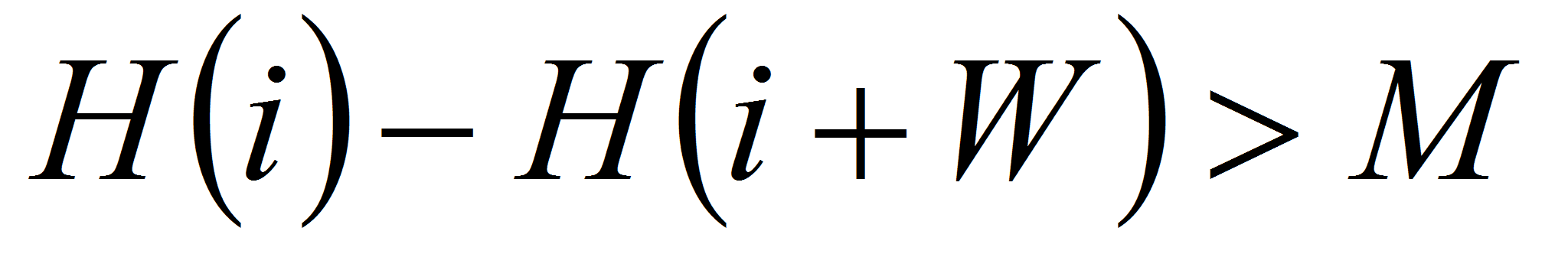- условие резкости максимума.
где 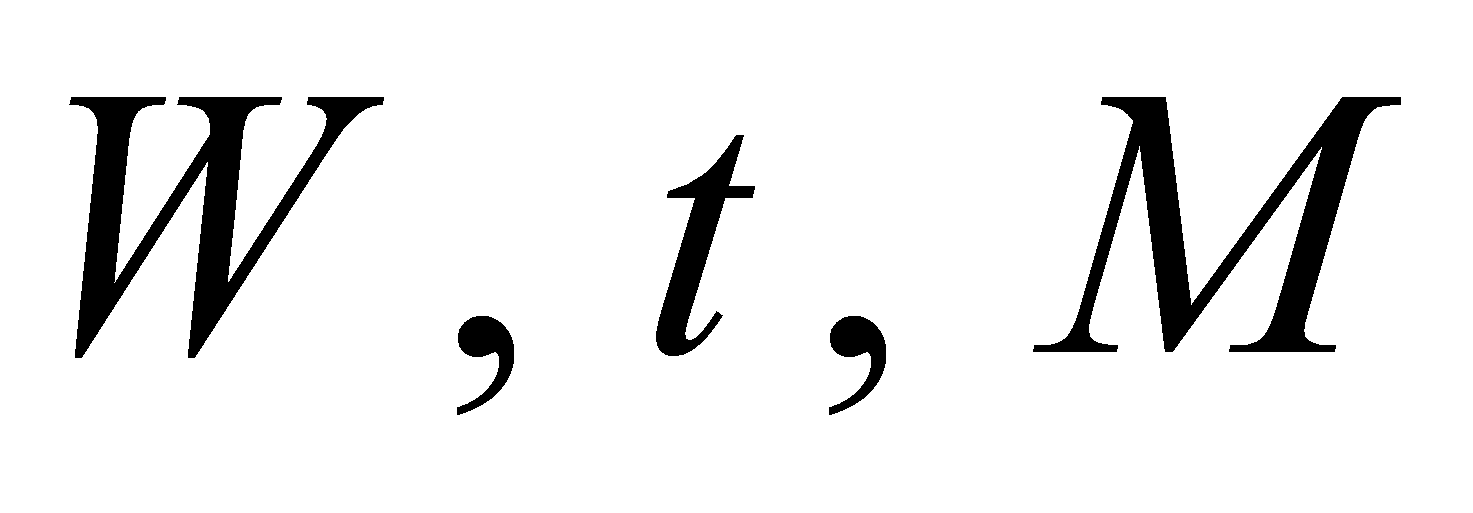- эмпирически подбираемые параметры (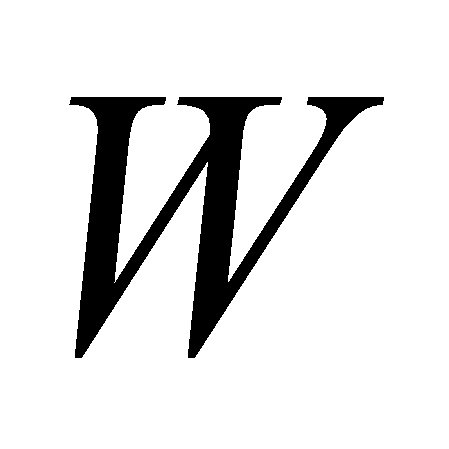- окно, 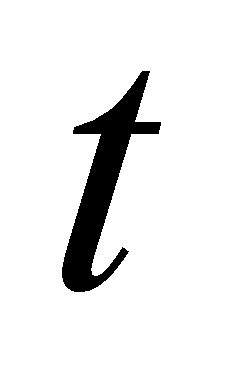- порог, 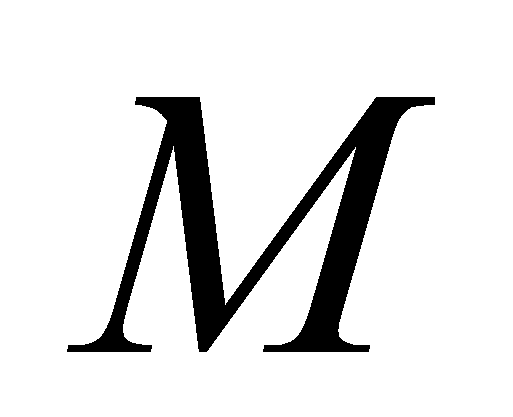- перепад). Подобное преобразование используется в [4] и в [5] - с фиксированным порогом.


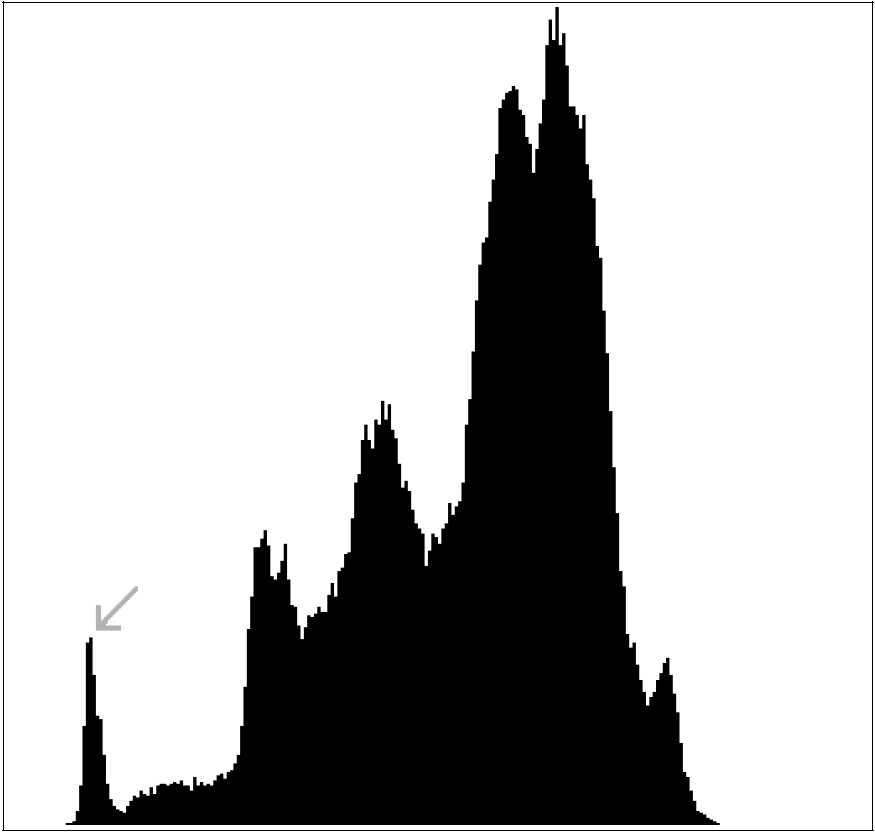
Рис.2. Гистограмма изображения, первый резкий максимум показан стрелкой.


Рис.3.Бинаризованное изображение.

Шаг 2. Проецирование на ось X.

Проецированием мы называем процедуру получения из бинарного изображения распределения количества точек с яркостью 1 в зависимости от координаты. В работе [7] также применяются проекции, но там проецируется само исходное изображение. Проекция — одномерный массив — получается из изображения по следующей формуле:

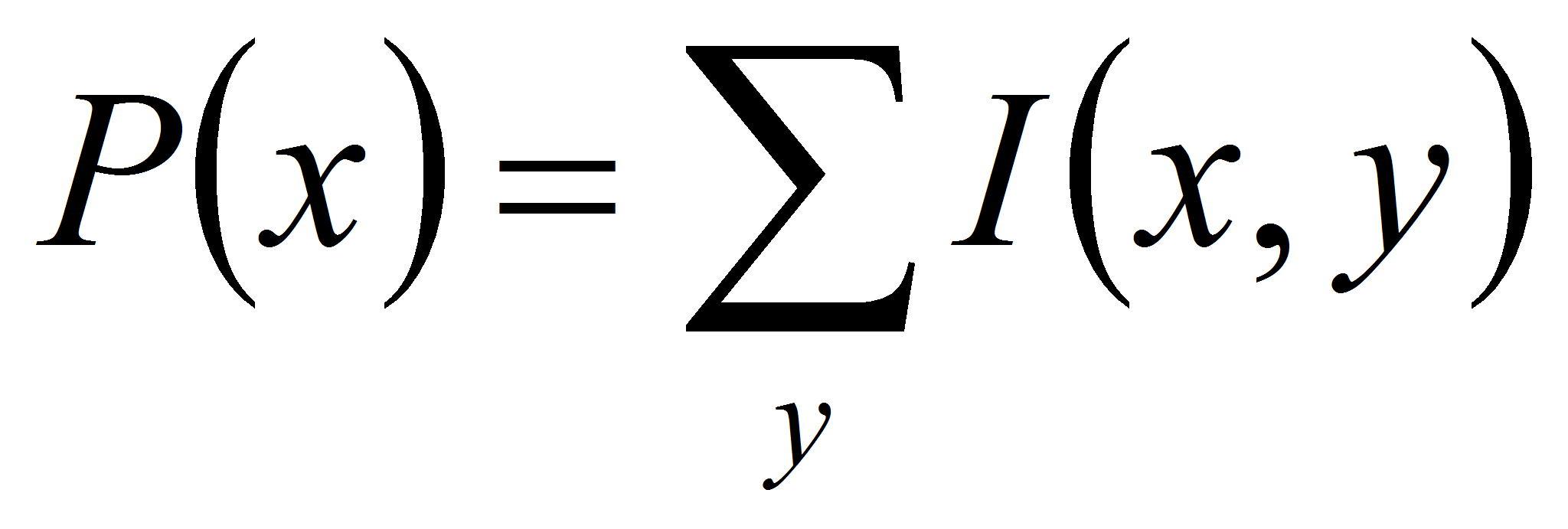
Предположение: максимум 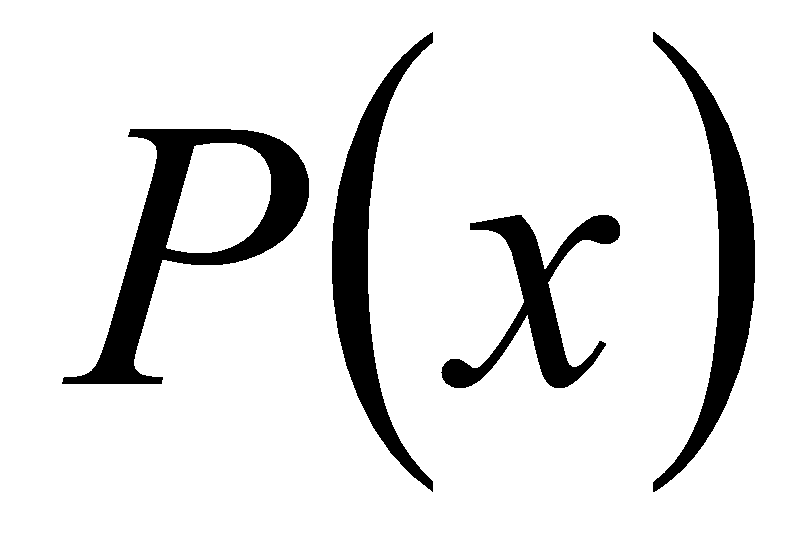располагается на координате, соответствующей центру зрачка.

Шаг 3. Поиск Y-координаты центра зрачка.

Для поиска 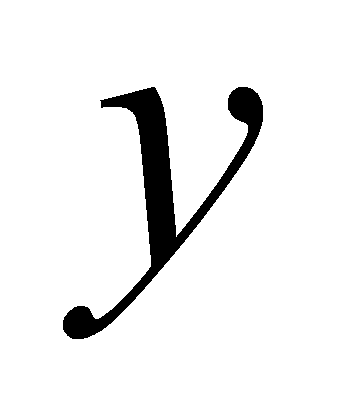-координаты этот метод оказался ненадёжным, так как зачастую максимум проекции на ось 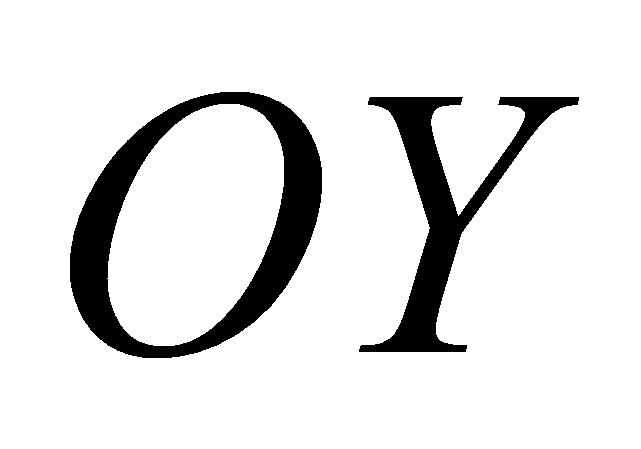доставляет не зрачок, а бровь или ресницы. Поэтому оценкой для координаты центра зрачка положим середину пересечения прямой 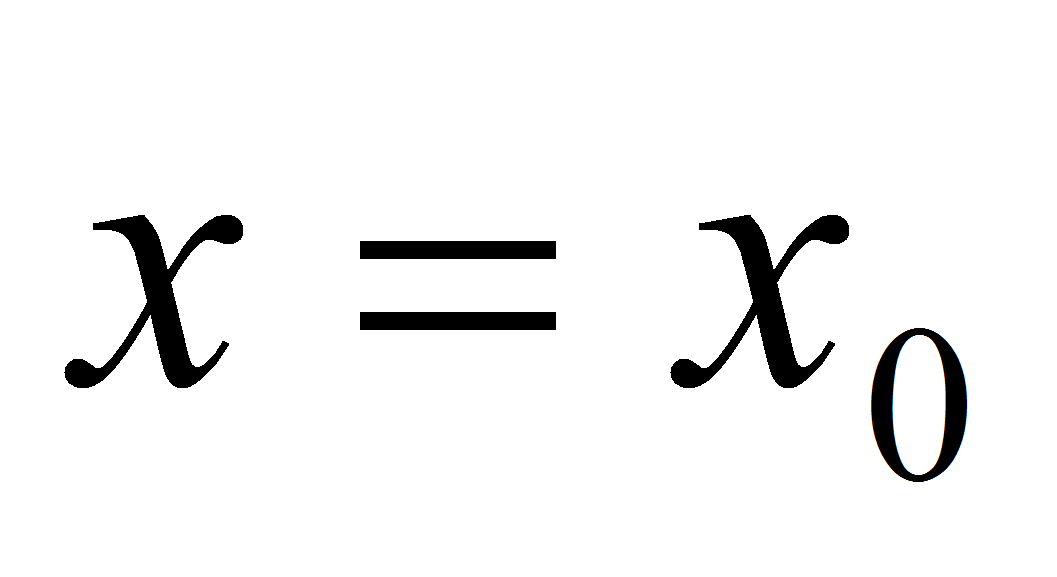с тёмной областью на бинаризованном изображении. Основанием для подобной оценки является то, что если максимум проекции на ось 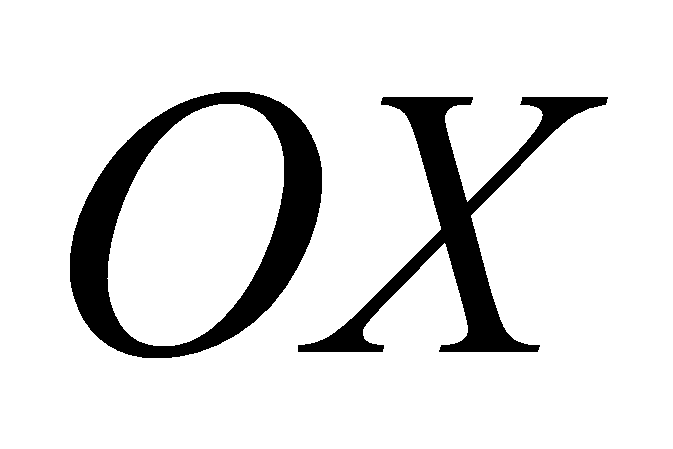достигается в середине зрачка, то середина этого пересечения будет расположена внутри зрачка.

Экспериментальная проверка

Проверка работы алгоритма производилась на открытых базах фотографий человеческих глаз:UBIRIS.v1 [10], CASIA-IrisV3 [15], ND-IRIS [12], BATH [16]. Истинные параметры зрачка на каждом изображении, проставленные экспертом, известны, с ними и сравнивается полученный результат. В таблицах 1-3 приведена статистика работы алгоритма. Для удобства восприятия выделены количества изображений, на которых разница между полученным и истинным значением меньше, чем десятая часть истинного радиуса зрачка; меньше половины радиуса зрачка; меньше радиуса зрачка.

Таблица 1 Статистика пересечений вертикальной прямой x=x₀ со зрачком

Название базы	Всего изображений	Количество пересечений в 10% от радиуса	Количество пересечений в 50% от радиуса	Количество пересечений со зрачком
ND-IRIS	64979	22430	62726	64701
BATH	13177	1486	12832	13081
CASIA	16180	8889	16058	16173
Всего	95513	40217	85577	93955

Таблица 2 Статистика пересечений вертикальной прямой y=y₀ со зрачком.

Название базы	Всего изображений	Количество пересечений в 10% от радиуса	Количество пересечений в 50% от радиуса	Количество пересечений со зрачком
ND-IRIS	64979	44714	64500	64875
BATH	13177	12164	13056	13093
CASIA	16180	13506	16121	16170
Всего	95513	71398	94842	95296


Этот метод показывает даже более высокую точность, чем определение -координаты зрачка.

Таблица 3 Статистика точности определения центра зрачка

Название базы	Всего изображений	Количество пересечений в 10% от радиуса	Количество пересечений в 50% от радиуса	Количество пересечений со зрачком
ND-IRIS	64979	15092	61751	64481
BATH	13177	1314	12686	13059
CASIA	16180	7225	15986	16164
Всего	95513	23727	91525	94864


Средняя по всем базам фотографий точность попадания результата: расстояние от истинного центра менее 10% от радиуса зрачка - 24,8%, менее 50% радиуса зрачка - 95,8%, менее радиуса зрачка - 99,3%.
Оценка сложности алгоритма. Оценка сложности при размерах изображения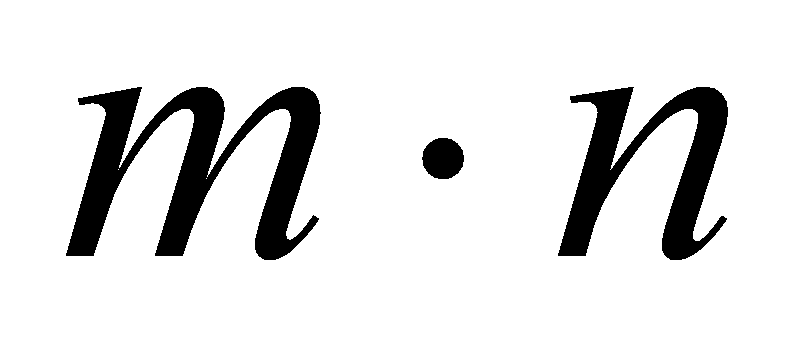, глубине цвета.
Гистограмма: 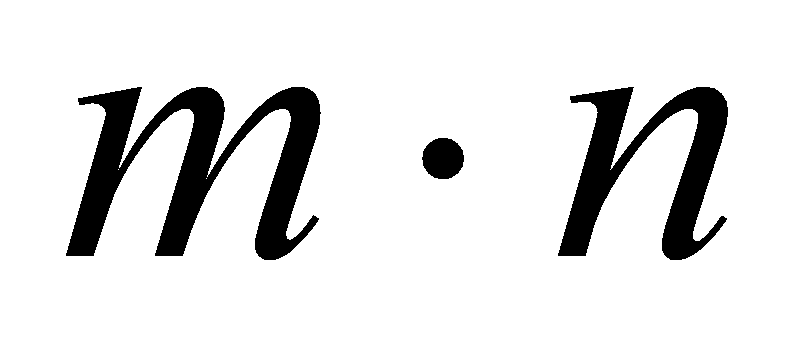операций сложения.
Поиск максимума гистограммы: 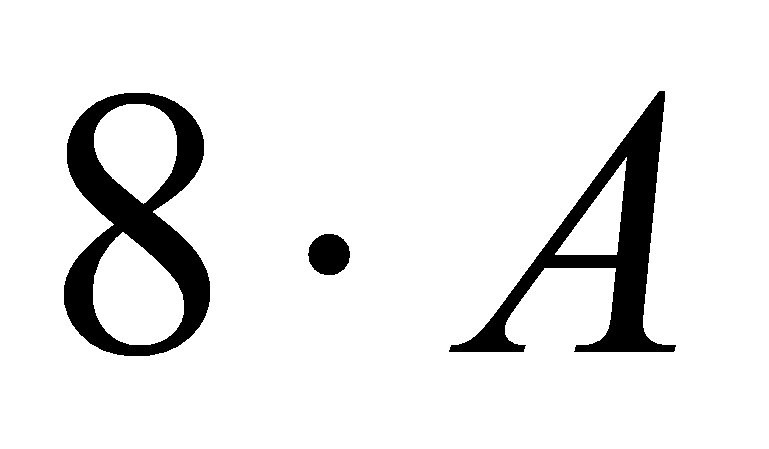операций сравнения.
Бинаризация: 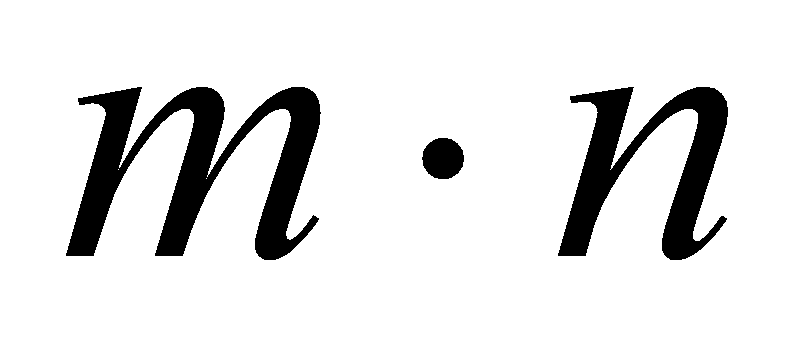операций сравнения и присваивания.
Проекция на ось 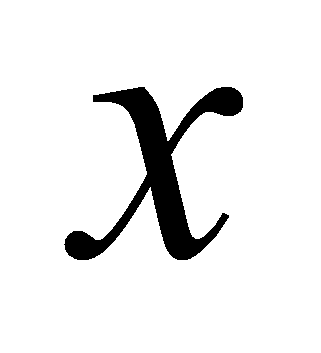: 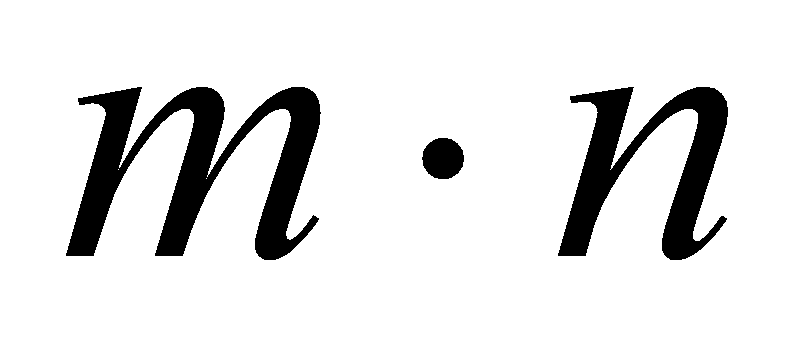операций сложения.
Поиск максимума по 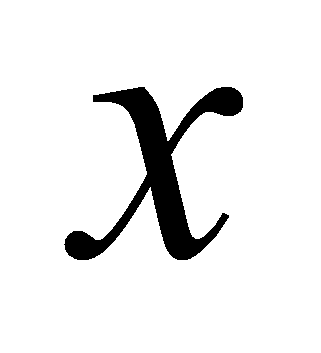: 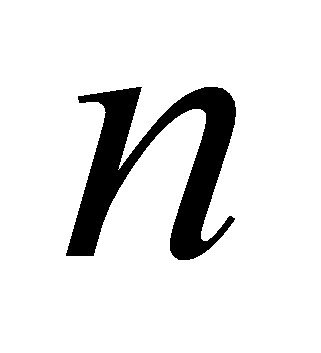операций сравнения.
Поиск 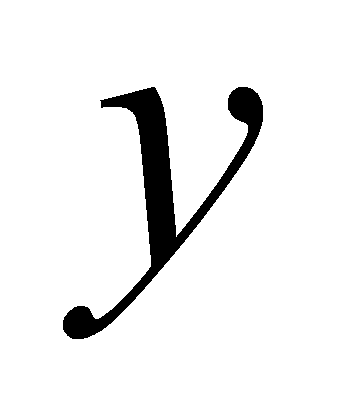-координаты: 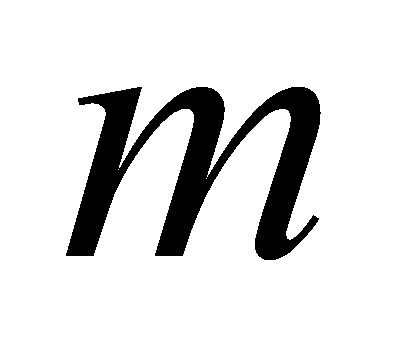операций сравнения и инкремента.
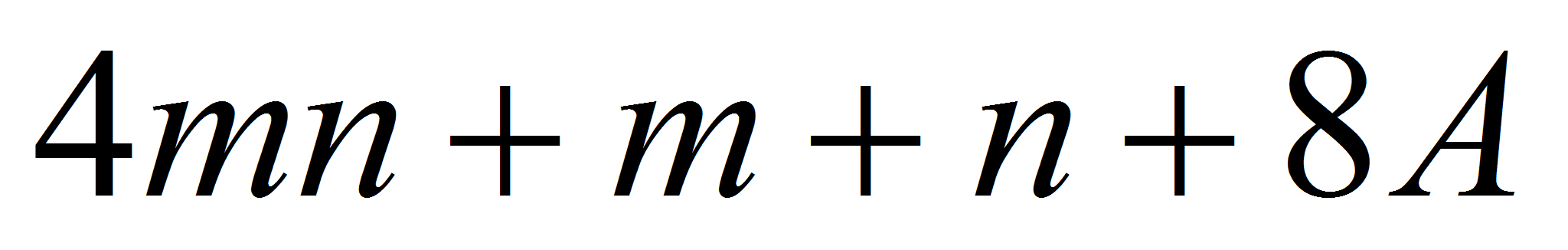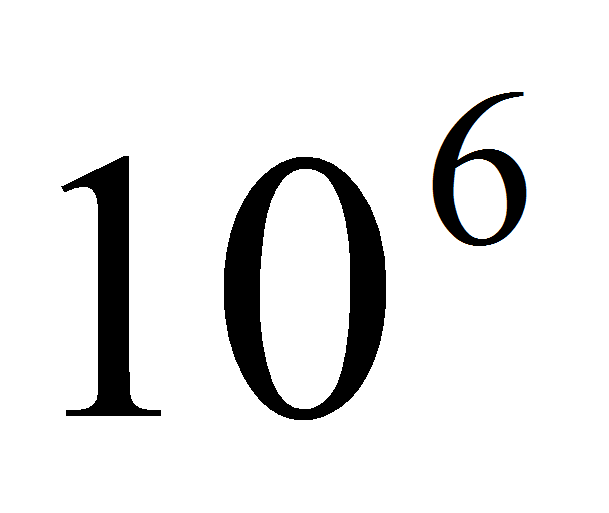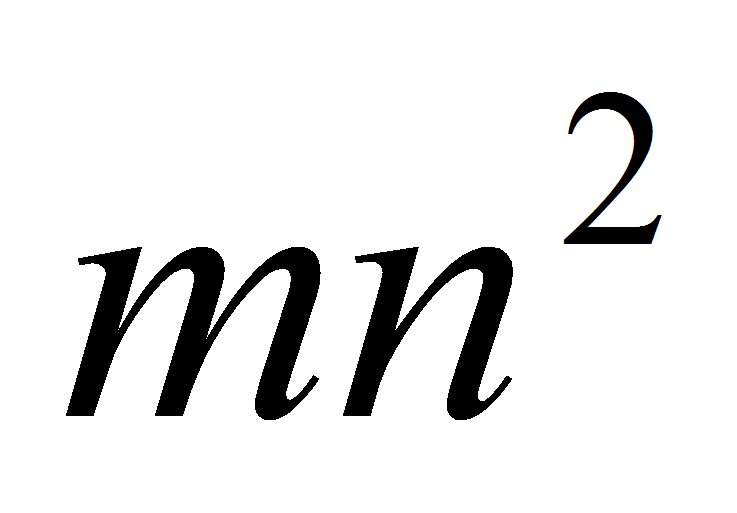Итого, если считать каждую операцию занимающей единицу вычислительного ресурса, то выходит . В нашем случае это около операций. Для сравнения, методы основанные на преобразовании Хафа или методе Даугмана, имеют минимальную сложность порядка , что даёт сложность порядка.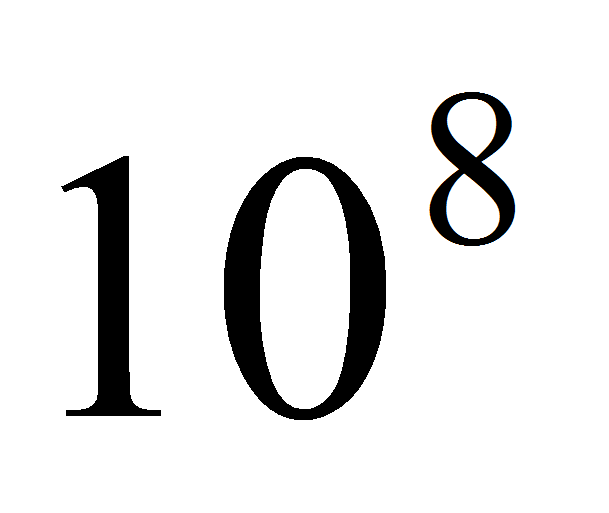
Анализ результатов. Метод показывает достаточно хорошую в большинстве случаев точность попадания внутрь зрачка, средняя по всем базам изображений (доля ошибок, то есть попаданий найденной точки за пределы зрачка, составляет 0,13%, а также небольшую сложность. При этом он не использует градиентного преобразования, поэтому качество результата нечувствительно к четкости изображения, но падает при плохой освещенности, когда тени на лице становятся такими же темными, как зрачок.Возникающие ошибки обычно связаны с неудачной бинаризацией, когда либо зрачок оказывается слишком светлым, как на Рис.4, или наоборот, в темную область включается значительная площадь ресниц или радужки, как на Рис.5.


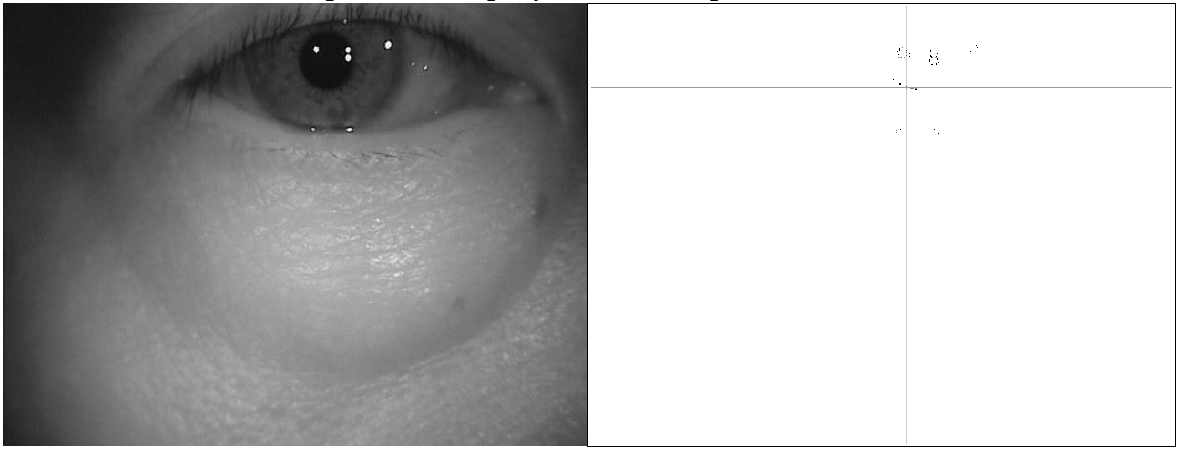
Рис.4.Пример некорректной обработки изображения.


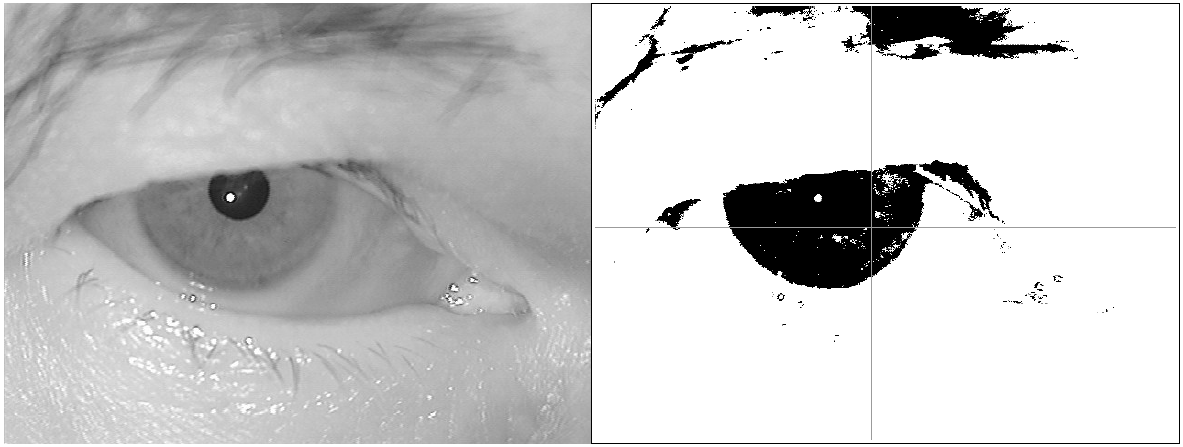
Рис.5.Пример некорректной обработки изображения.

В дальнейшем необходимо изучить возможность улучшения частоты попадания внутрь зрачка, а еще лучше - в 50% радиуса зрачка. Это позволит использовать результат для дальнейшего уточнения параметров зрачка. Также нужно построить критерии оценки результата, позволяющие отбраковывать заведомо неверные варианты, предлагаемые алгоритмом.

Литература:

[1] Daugman J. http://www.cl.cam.ac.uk/ jgd1000/
[2] Xu L., Oja E., Kultanan P. A new curve detection method: Randomized Hough transform (RHT). // Pattern Recog. Lett. 1990. N11. P.331-338.
[3] Rad A.A., Faez K., Qaragozlou N. Fast Circle Detection Using Gradient Pair Vectors. // Proc. 7th Digital Image Computing: Techniques and Applications. 2003. P.879-887.
[4] Boyd M., Carmaciu D., Giannaros F., et al MSc Computing Science Group Project Iris Recognition. // Imperial College, London. 2010.
[5] Dey S., Samanta D. A Novel Approach to Iris Localization for Iris Biometric Processing. // Int. J. Biological and Life Sciences. 2007. N3. V.3.
[6] Матвеев И.А., Ганькин К.А. Распознавание человека по радужке // Системы безопасности. 2004. N.5. P.72-76.
[7] Zhou Z.-H., Geng X. Projection functions for eye detection. // State Key Laboratory for Novel Software Technology, Nanjing University. 2002.
[8] Moravcik T. An Approach to Iris and Pupil Detection in Eye Image. // University of Zilina. 2010.
[9] Гонсалес Р., Вудс Р. Цифровая обработка изображений // М.:Техносфера. 2005. 1072 с.
[10] Proenca H., Alexandre L. UBIRIS: A noisy iris image database. // 13th Int. Conf. Image Analysis and Processing. P.970-977. Cagliari, Italy. Springer.
[11] ISO/IEC 19794-6 Information technology - Biometric data interchange formats -
Part 6: Iris image data.
[12] Phillips P., Scruggs W., O'Toole A. et al Frvt2006 and ice2006 large-scale experimental results. IEEE PAMI. 2010. N.32. V.5. P.831-846.
[13] Матвеев И.А. Метод поиска окружности с известной внутренней точкой на изображении. // Труды ИСА РАН. Динамика неоднородных систем. 2007. №31. Т.1. С.288-293.
[14] Бирич Т.А., Марченко Л.Н., Чекина А.Ю. Офтальмология. // Минск. Вышэйшая школа. 2007. 576 с.
[15] Chinese Academy of Sciences Institute of Automation. Iris image database, version 3. (2005) Available from http://www.cbsr.ia.ac.cn/IrisDatabase.htm
[16] University of Bath. Iris Image Database. (2005) Available from http://www.bath.ac.uk/elec-eng/research/sipg/irisweb/

Основные термины (генерируются автоматически): BATH, CASIA, ND-IRIS, зрачок, изображение, радиус зрачка, операция сравнения, пересечение, радужная оболочка, темная область.

Метод проекций яркости при поиске зрачка на изображении

Библиографическое описание:

Похожие статьи

Методы определения объектов на изображении

Кластеризация эталонов радужки как метод оптимизации поиска...

Исследование и применение eye-tracking технологии на человеке

Сравнительный анализ прямой и содружественной реакций...

Береги зрение смолоду

Распознавание световых пятен лазера на изображении

Анализ методов и систем регистрации окуломоторной активности

Исследование механизмов защиты цифровой видеоинформации...

Методы распознавания образов | Статья в журнале...