Математическая модель горения пропан-бутановой смеси при недостатке окислителя в диффузионной горелке

Для идентификации процессов протекающих при сжигании топлива в горелочных устройствах необходимо спрогнозировать ход и параметры гидродинамических и тепло-массообменных процессов. Моделирование течения с горением является наиболее сложной задачей движения газа. Данная проблема может эффективно решаться в системе вычислительной гидродинамики FlowVision. FlowVision решает задачи внешней и внутренней аэро-гидродинамики, в частности, задачи диффузионного горения и горения предварительно подготовленных топливных смесей. Последнее обстоятельство является основным при выборе этой системы для моделирования процесса сжигания топливных компонент в диффузионной горелке с «реальными» размерами и расходами газов.

Виртуальный эксперимент в системе вычислительной аэро-гидродинамики, в отличие от натурных испытаний, значительно снижает трудоемкость подготовительных мероприятий, упрощает экспериментальную часть работы, более наглядно и детально раскрывает суть происходящих процессов.

Модель горения в системе FlowVision включает расчет конечно-объемным методом параметров процесса по уравнениям:

- Навье-Стокса (закон сохранения импульса);

- неразрывности (закон сохранения массы сплошной среды);

- закона сохранения энергии, записанного через энтальпию;

- переноса реагентов в приближении брутто-реакции (перенос топлива, окислителя и продуктов сгорания);

- k-&#; модели турбулентности.

Эта модель представляет собой развитие модели течения слабосжимаемой жидкости со всеми ее ограничениями, но при этом учитывается горение газовой смеси. Предполагается, что газовая смесь может быть предварительно перемешана и не перемешана. Ограничения модели предполагают течение с любыми изменениями плотности среды (однако числа Маха все равно малы – т.е. изменения плотности обусловлены только температурными эффектами или влиянием примесей в газе).

При решении задач в FlowVision дифференциальные уравнения аппроксимируются на расчётной сетке в предположении, что каждая ячейка представляет собой конечный объём, в котором скорости изменения физических величин сбалансированы потоками этих величин через грани ячейки. Для расчета используется прямоугольная сетка с локальным измельчением расчетных ячеек у криволинейных границ, кромок и граничных областей малого размера.

Решение конкретных задач во FlowVision предполагает создание трехмерной модели реального объекта во внешней системе автоматизированного проектирования (AutoCAD, ParaSolid, SolidWorks, T-Flex и др.) с последующим импортом геометрии в препроцессор FlowVision. В препроцессоре реализуется интерактивное задание граничных условий на поверхностях модели, диагностика и трансформация геометрии. Далее следуют этапы:

- выбор математической модели (в нашем случае – Модель горения);

- задание граничных условий;

- задание исходной расчетной сетки и критериев её адаптации по решению и по граничным условиям;

- задание параметров расчетного метода;

- проведение расчета (без участия пользователя);

- просмотр результатов расчета по выбранным параметрам в графической форме;

- оценка точности расчетов методом сходимости по сетке.

Блок расчета уравнений и постпроцессор (часть программы, в которой анализируются результаты расчета) объединены и работают одновременно. Это позволяет проводить моделирование и одновременно анализировать результаты, менять граничные условия и параметры математической модели.

Для моделирования процесса в диффузионной горелке с кольцевым соплом для подачи воздуха построена ее 3D-модель в системе T-Flex CAD 3D (рис. 1).

Рисунок 1 – Разрез 3D-модели диффузионной горелки

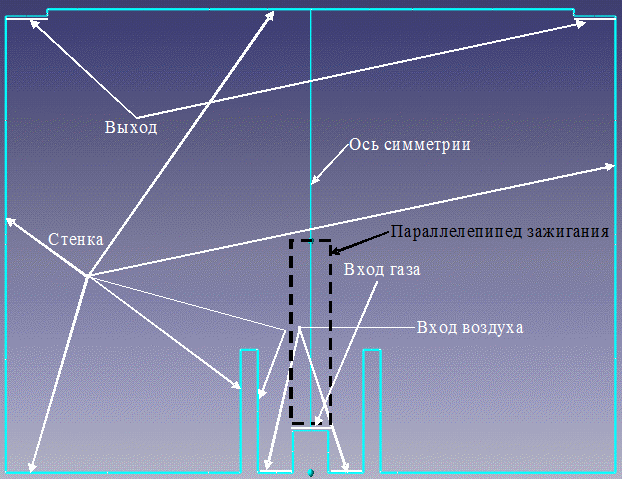
Геометрия из T-Flex CAD экспортировалась через обменный формат Stereo Lithography (stl) и подгружалась в систему FlowVision. В препроцессоре выбиралась осесимметричная задача, устанавливались начальные параметры соответствующие нормальным условиям, из стандартной библиотеки загружались свойства компонентов, подаваемых на горение (воздух и пропан-бутан), и свойства продуктов сгорания для заданной смеси, создавался фильтр одноразового зажигания в параллелепипеде и задавались граничные условия (названия границ указаны стрелками на рис. 2).

В качестве начальных значений и физических параметров модели задавались начальная температура T=293 К; давление 101325 Па; пульсация 0,03; масштаб турбулентности 0,01 м, стехиометрический коэффициент k_m=15,67 (для топливной смеси пропан-бутан + воздух); температура воспламенения 750 К; диапазон коэффициента избытка окислителя в котором горение поддерживается самопроизвольно &#;=0,02 – 3, выбиралась пульсационная модель химической кинетики процесса.

Рисунок 2 – Граничные условия при моделировании процесса в диффузионной горелке

Использовались следующие параметры для границ и источника зажигания в примере расчета форсированных режимов горения (с высоким выходом углеродного депозита при &#;=0,4; k_m=6,9):

- «Стенка» – тип границы – «Стенка», логарифмический закон изменения скорости;

- «Вход газа» – тип границы – «Вход/Выход», температура 20 ^оС, концентрация 1, нормальная массовая скорость 0,1139&#;10^-4 кг/(м²&#;с);

- «Вход воздуха» – тип границы – «Вход/Выход»; температура 20 ^оС, концентрация 0, нормальная массовая скорость 0,10834 кг/(м²&#;с);

- «Выход» – тип границы – «Свободный выход»;

- «Параллелепипед зажигания» – для расчета «холодного» течения – «Неактивный», для расчета горения – «Одноразовый».

Для расчетной подобласти генерировалась начальная прямоугольная сетка с разбиением на 50 участков по координатным осям.

Процесс моделирования включал два этапа. На первом рассчитывалось «холодное» течение газовых компонент без горения. При этом обеспечивалось некоторое распределение коэффициента избытка окислителя &#; внутри горелки, при котором горючее достигает границы «Выход».

После того как было получено распределение коэффициента избытка окислителя, проводилась инициация процесса горения в «параллелепипеде зажигания» с использованием подготовленного фильтра зажигания (переключение режима «Неактивный» в режим «Одноразовый»).

Расчет проводился до стационарного состояния, которое контролировалось по погрешности основных расчетных переменных (точность расчета 10^-4).

Для диффузионной горелки с заданным расходом горючего и окислителя получены распределения коэффициента избытка окислителя (рис. 3), скоростей (рис. 4) и температуры (рис. 5).

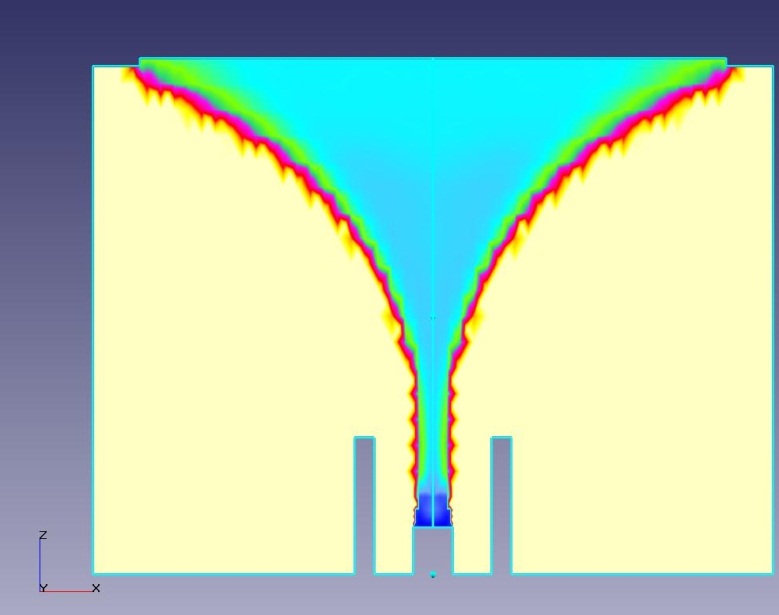
Рисунок 3 – Распределение величины коэффициента избытка окислителя &#;

в сечении диффузионной горелки

Рисунок 4 – Векторное поле модуля скорости в сечении диффузионной горелки

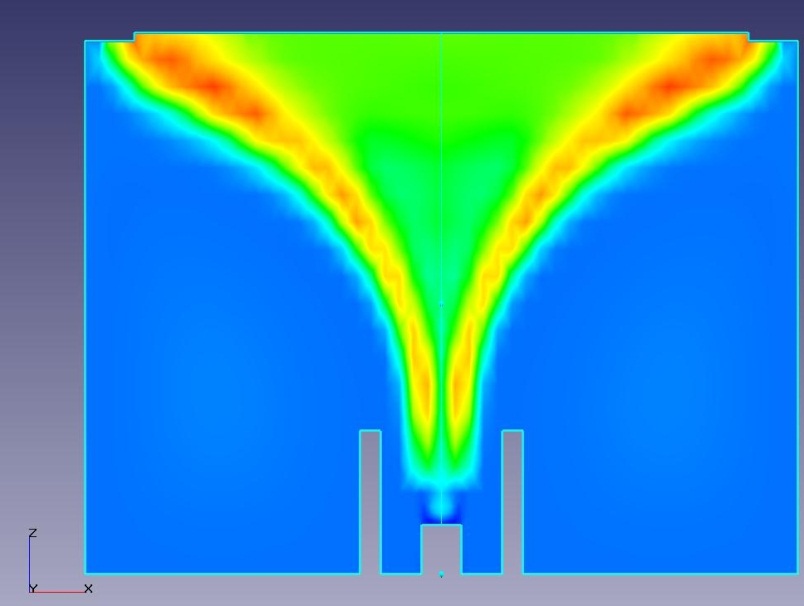
Рисунок 5 – Температурное поле в сечении диффузионной горелки

Анализ результатов моделирования показывает, что в горелке при раздельной подаче горючего и окислителя с заданными параметрами наблюдается неоднородное смесеобразование с коэффициентом избытка окислителя близким к стехиометрическому вблизи границы расширяющегося «конуса», образованного истекающим из центрального сопла горючим. Область богатой топливной смеси, в которой может образовываться углерод в конденсированной фазе, сосредоточена в конусе под центральной частью подложки-саженакопителя.

На векторном поле скоростей видно, что по периферии наблюдается циркуляция потока продуктов сгорания (не происходит проскок компонентов топливной смеси без реагирования). Т.е в установившемся режиме можно эффективно регулировать соотношение окислитель/горючее, варьируя их расход на входе в горелку.

На подложку-саженакопитель при заданных расходах поступают продукты сгорания с разной температурой.

Следует отметить, что при более мягких режимах горения с меньшим расходом компонентов пламя имеет фактически цилиндрическую форму от среза сопла и расширяется на конус малой высоты только вблизи подложки-саженакопителя. При этом диаметр конуса в области сечения подложки-саженакопителя зависит от расходов газовых компонент.

Литература:

1. Польшиков, В.Ю. Разработка технологии и оборудования для синтеза углеродных наноструктурных материалов в диффузионном пламени / В.Ю. Польшиков // Проблемы техногенной безопасности и устойчивого развития: сборник научных статей молодых ученых, аспирантов и студентов. Тамбов: изд-во ГОУ ВПО ТГТУ. – Вып. II. 2011 – С .202-206.

2. Борунова, А.Б. Получение углеродных наночастиц при горении метана / А.Б. Борунова, Ю.В. Григорьев, К.Я. Трошин // Горение и взрыв. – М.: ТОРУС ПРЕСС, 2008. – С. 10-13.