Статья посвящена возможностям использования аппарата искусственного интеллекта в геологии, а именно при автокорреляции разрезов скважин. Так же в статье описываются результаты работы модуля по автокорреляции скважин, основанной на самоорганизующихся картах Кохонена.
В настоящее время, когда повышается необходимость эксплуатации все более сложнопостроенных объектов, появляется необходимость обоснованного и правильного выделения пластов. В случае если продуктивные пласты не осложнены зонами выклинивания и замещения процесс корреляции занимает небольшое количество времени и носит формальный характер. Но когда месторождения многопластовые, вскрыты большим количеством скважин, осложнены зонами глинизации и выклинивания коллектора в таких случаях выделение подсчетных объектов бывает не однозначным и спорным, и вместе с тем, занимает большое количество затрат времени и трудовых ресурсов.
Одним из важнейших проектных документов позволяющим недропользователю эксплуатировать месторождение является подсчет запасов (ПЗ) нефти и газа. В свою очередь одним из первых и важнейших этапов ПЗ является корреляция разрезов скважин.
Корреляцию при составлении проектного документа выполняют специалисты геологи вручную либо с помощью определенных программ, которые определяют одноименные пласты в скважинах. Данная статья посвящена таким программным комплексам (ПК), а точнее методам, с помощью которых это можно сделать наиболее эффективно в случае, когда необходимо коррелировать большое количество скважин.
Корреляция при подсчете запасов больших месторождений (таких как Приобское, Мамонтовсвкое, Малобалыкское, Правдинское) занимает большое количество времени, поэтому применение ПК будет значительно упрощать процесс, геолог будет только корректировать результат (некоторый субъективизм всегда присутствует), либо процесс корреляции.
Одним из математических методов, с помощью которого можно обрабатывать большое количество данных являются нейронные сети. Аппарат нейронных сетей успешно используется для решения задач нефтяной геологии. Главный положительный эффект заключается в том, что нейронные сети могут решать сложные задачи с учетом большого количества разнородных исходных данных.
Искусственные нейронные сети представляют собой устройства параллельных вычислений, состоящие из множества взаимодействующих простых процессоров - нейронов. Эти процессоры исключительно просты и их вычислительная возможность ограничивается некоторым правилом комбинирования входных данных и правилом активации, позволяющие вычислить выходной сигнал по совокупности входных данных.
Один из самых главных аспектов использования нейронных сетей заключается в том, что хотя элементы такой сети имеют очень ограниченные вычислительные возможности, вся сеть в целом оказывается способной выполнять сверхсложные задачи.
Решение на основе нейронных сетей может выглядеть и вести себя как обычное программное обеспечение, но различие состоит в том, что реализации на основе нейронных сетей «обучается», а не программируется: сеть сама учится выполнять задачу, а не программируется непосредственно.
Для каждого элемента сети имеется правило суммирования поступающих сигналов и правило вычисления выходного сигнала, посылаемого затем другим элементам сети. Правило вычисления выходного сигнала называется функцией активности. Обучение нейрона заключается в измерении значений весовых коэффициентов. В ходе обучения величина, на которую должен измениться весовой коэффициент, вычисляется с помощью соответствующего правила.
Авторами была разработана методика, реализованная в программном комплексе «GeoGlobe», основанная на применении нейронных сетей, с помощью которой проводится автоматическая корреляция разрезов скважин. В качестве базового алгоритма предложенной методики были использованы самоорганизующиеся карты Кохонена. [1]
Самоорганизующиеся карты Кохонена отличаются от обычной нейронной сети тем, что при обучении «классической» многослойной нейросети на вход подаются данные или индикаторы, а выход нейросети сравнивается с эталонным значением. Разность этих значений называется ошибкой нейросети, которая и минимизируется в процессе обучения. Таким образом, обычные нейросети выявляют закономерности между входными данными и прогнозируемой величиной.
В процессе обучения карт Кохонена на входы также подаются данные и индикаторы, но при этом сеть подстраивается под закономерности во входных данных, а не под эталонные значения выхода. Такое обучение называется обучением «без учителя». Обучение при этом заключается не в минимизации, а в подстройке внутренних параметров нейросети (весов) для большего совпадения с входными данными. После обучения такая нейросеть визуально отображает многомерные входные данные на плоскости нейронов. Имея такое представление данных, можно очень наглядно увидеть наличие или отсутствие взаимосвязи во входных данных.
Для большего удобства визуального представления нейроны карты Кохонена располагают в виде двухмерной матрицы и раскрашивают эту матрицу в зависимости от анализируемых параметров нейронов.
Как и при работе с обычными нейросетями, оперирование картами Кохонена складывается из нескольких последовательных этапов. Первым из них является этап определения состава входов.
Для хорошего обучения нужно выбрать такое множество входов, которое наиболее сильно влияет на выходные (прогнозируемые) значения. Если мы угадали, и входы действительно влияют на выход, то нейросеть будет работать и давать отличные прогнозы. Однако подобрать правильные входы сложная задача. Обычно это делается методом проб и ошибок, т.е. простым перебором различных комбинаций индикаторов и данных [2].
Входы нейросети, обучаемой «без учителя», определяются другим образом, и перед такой нейросетью ставится иная цель – выявление закономерностей между любыми входными данными и индикаторами, которые и подаются на вход карты. Архитектура карт Кохонена в отличие от многослойной нейронной сети, очень проста и представляет собой один слой нейронов, который организован в виде двухмерной матрицы. Пользователю необходимо определить лишь размер этой матрицы. Так как это двухмерная матрица, то ее очень удобно отображать в виде «карты» с определенной заливкой, зависящей от анализируемого параметра нейрона.
В процессе обучения на вход такой нейросети последовательно подаются обучающие примеры. После подачи очередного примера определяется наиболее схожий нейрон, т.е. нейрон, у которого скалярное произведение весов и поданного на него вектора минимально. Такой нейрон считается победителем и призван быть центром при подстройке весов у соседних нейронов. Правило обучения, предложенное Кохоненом, предполагает соревновательное обучение с учетом расстояния нейронов от «нейрона-победителя» и записывается в виде:
где Λ(|i-i*|) – функция соседства, определяющая величину корректировки веса нейрона, Wi – вес i-ого нейрона, β – скорость обучения.
Для нейрона-победителя функция соседства равно 1 и затем плавно (по линейному или экспоненциальному закону) уменьшается при удалении от него. Таким образом, в процессе обучения подстройка весов происходит не только в одном нейроне, но и в его окрестностях.
После завершения процесса обучения карта Кохонена классифицирует входные примеры на группы схожих друг с другом. Вся совокупность нейронов в выходном слое точно моделирует структуру распределения обучающих примеров в многомерном пространстве. [3]
Для анализа работы нейросети использовалось Правдинское нефтяное месторождение, представленное 12 пластами. Нами были выбраны два пласта – БС8 и БС9 (рисунок 1), по причине того, что они залегают близко друг другу, и имеют примерно одинаковую фациальную обстановку осадконакопления, вследствие чего, коррелировать данные разрезы пластов сложно, но это позволяет максимально использовать аппарат нейронных сетей.
Р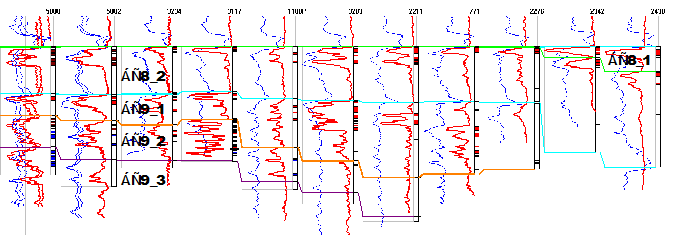
ис.
1 – Корреляционная схема залегания пластов БС8 и БС9
Правдинского месторождения (маркеры поставлены специалистом геологом)
Исходные данными для анализа являются следующий кривые ГИС: ПС (метод собственной поляризации), ИК (индукционный каротаж), ГК (гамма каротаж), а так же в роли ориентировки - абсолютная отметка глубины скважины. При корреляции каждая кривая имеет свой вес (задается пользователем), т.е. определенное влияние на результат.
В результате получены маркеры на скважинах отбивающие пласты БС8 и БС9 (рисунок 2). При сравнении в маркерами, поставленными геологом выяснилось, что они совпадают в 64% случаях. Это расхождения объясняется наличием зон выклинивания и замещения, в которых на кривых ГИС практически нет аномалий. Поэтому при корреляции необходимо так же учитывать особенности осадконакопления, в частности карты трендов изменения общих толщин пластов.
Р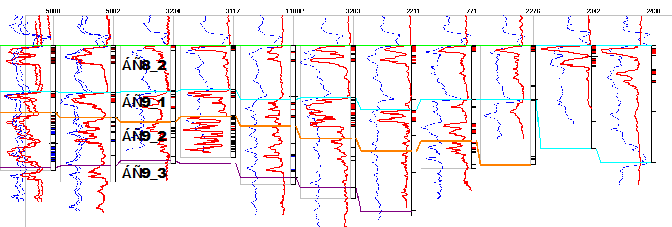
ис.
2 – Корреляционная схема залегания пластов БС8 и БС9
Правдинского месторождения (маркеры поставлены с помощью нейросетей)
В заключение необходимо добавить, что развитие информационных наук в настоящее время достигло такой степени, что ее активное применение в различных сферах науки позволит значительно автоматизировать многие процессы и операции, что в свою очередь позволит сэкономить время и трудозатраты на выполнение той или иной работы.
Литература:
- Методы нейроинформатики / Под. ред. А.Н. Горбаня; отв. за выпуск М.Г. Доррер. КГТУ, Красноярск, 1998. 205 с.
- Anil K. Jain, Jianchang Mao, K.M. Mohiuddin/Artificial Neural Networks: A Tutorial, Computer, Vol.29, No.3, March/1996, pp. 31-44.
- Генетические алгоритмы, искусственные нейронные сети и проблемы виртуальной реальности/ Г.К. Вороновский, К.В. Махотило, С.Н. Петрашев, С.А. Сергеев. – Х.: ОСНОВА, 1997. – 112 с.

