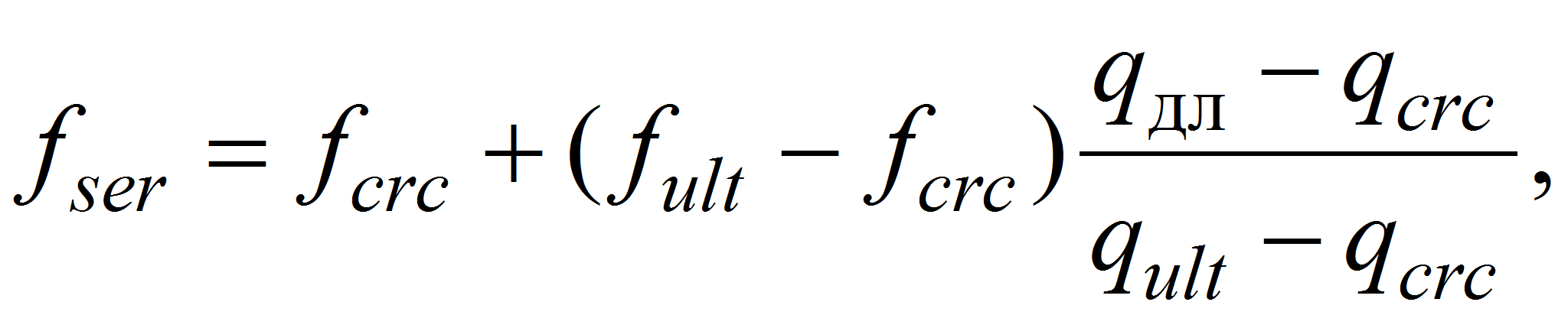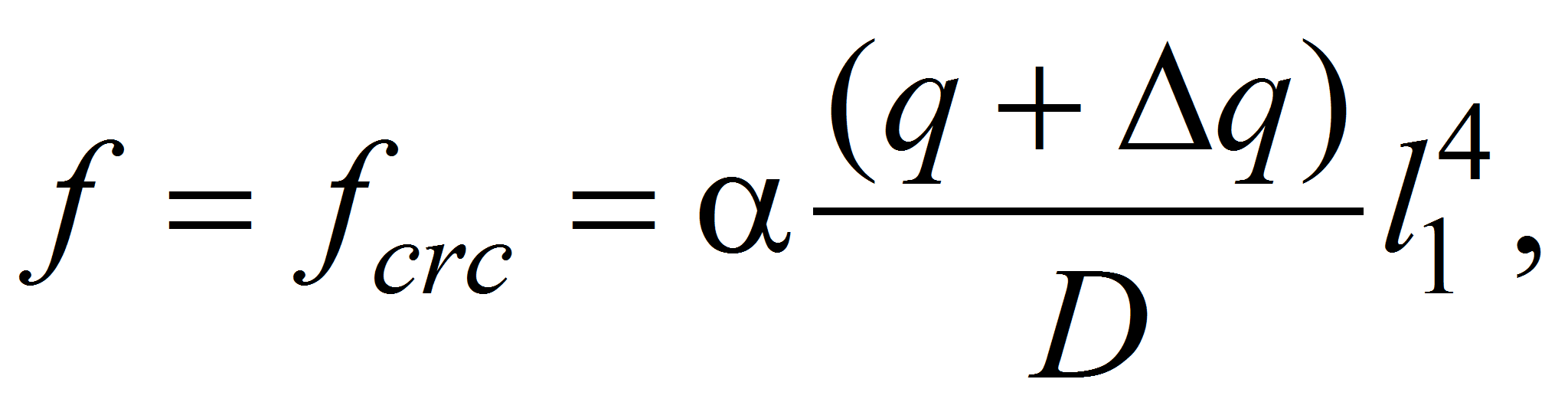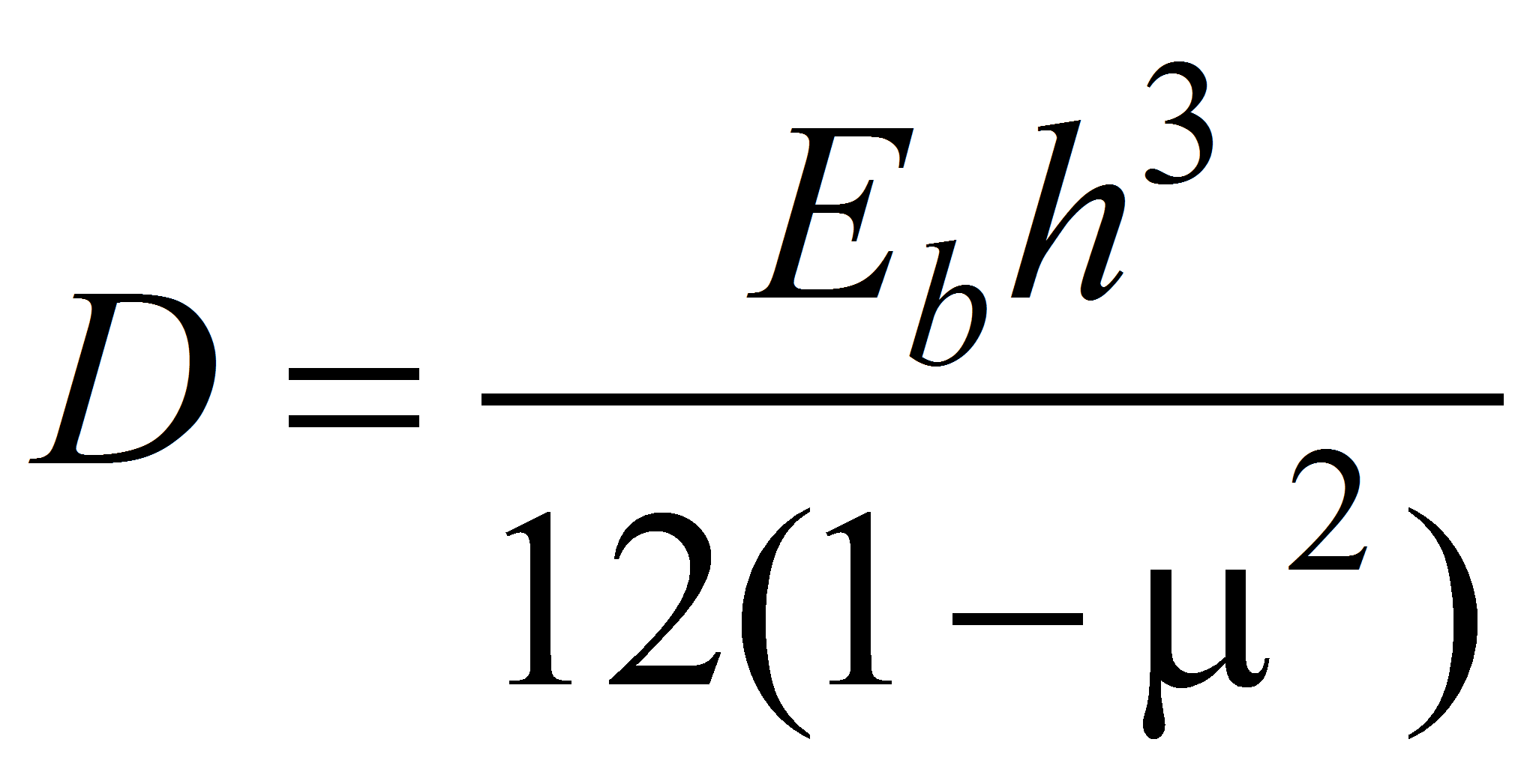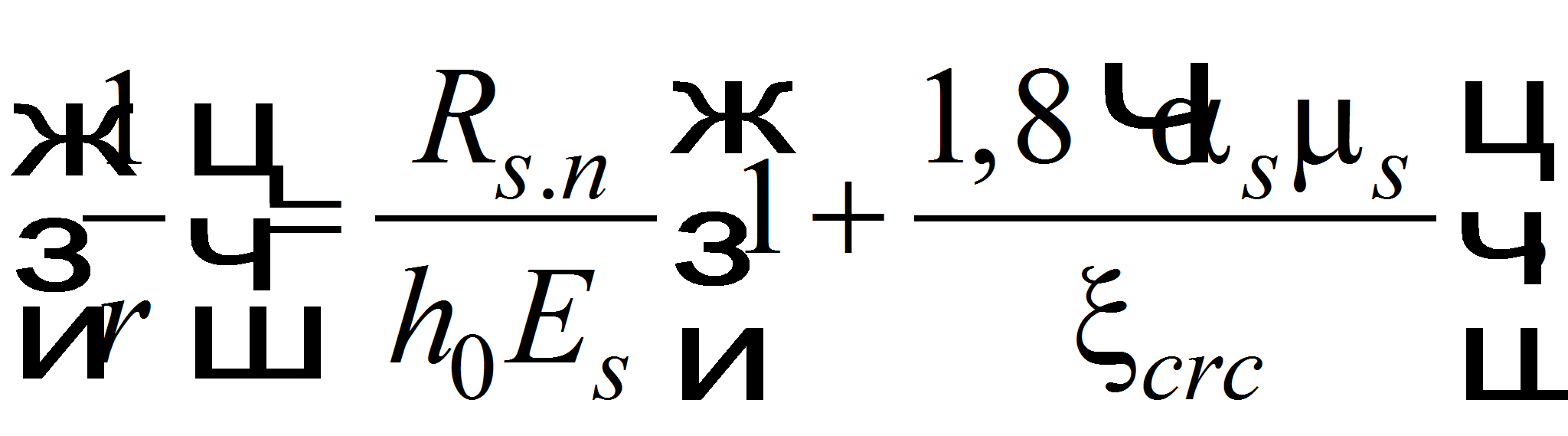Катастрофы в строительстве случаются в наше время по различным причинам. Основной предвестник - предсказуемость и другие физические свойства искусственных катастроф были подробно рассмотрены и табулированы в работе Скоробогатова С.М., Хомякова В.А, Морданова О.Н. и Мордановой Е.С. «Классификация катастроф железобетонных конструкций» [1]. Один из возможных способов их предотвращения – правильный расчет зданий и сооружений.
Плиты с отверстием применяются при возведении многих конструкций, таких, как элеваторы, бункера, холодильники, многоэтажные промышленные здания с вертикальной технологией производства, жилые и общественные здания, насыщенные различными коммуникациями.
К сожалению, в нашей литературе пока ещё недостаточно освещаются вопросы расчета плит с отверстием, что затрудняет использование достигнутых в теории результатов и зачастую приводит к применению приближенных приемов.
Примером может служить расчет пластин методами граничной коллокации [2], результат исследований О. В. Машкина и д. ф.-м. н., проф. В. В. Рогалевича – метод, реализуемый для конкретных параметров пластины, позволяет получить надежное приближенное решение в виде формулы в задачах изгиба, числа и формулы в задачах устойчивости. Он основан на простой аппроксимации функций прогиба, определении одной константы решения из условия ортогональности невязки с аппроксимирующей функцией, отыскании корректирующих параметров из условия минимума среднеквадратических интегральных невязок в задачах изгиба или минимума сжимающего усилия в задачах устойчивости.
Для избежания двойственности в расчете конструкций, когда определение усилий производится методами теории упругости, а подбор сечений элементов выполняется по предельному состоянию, необходимо определить возможность сочетания двух научных направлений: упругая работа пластин вокруг отверстий и виртуальная работа пластин с линейными пластическими шарнирами. Ещё одним важным вопросом является возможность корреляции величин между этими двумя состояниями для определения прогибов реальных конструкций.
Расчет плиты с отверстием по методу предельного равновесия помогает решить эту задачу. В работе Р. В. Зиновьевой, Н. Ф. Зиновьева, А. М. Фрактера [3] изложены результаты экспериментально-теоретических исследований железобетонных плоских плит, ослабленных отверстием, анализируются схемы излома в зависимости от места расположения отверстия и излагаются методы расчета квадратных, прямоугольных и круглых плит с отверстием различной формы при разных условиях опирания. Примерами, приведенными в книге, подтверждается, что расчет плит с отверстием по методу предельного равновесия не представляет трудностей и к тому же дает существенную экономию арматурной стали. Так, для рассчитанных плит эта экономия составила около 24 %.
Для расчета плиты с отверстием применен кинематический способ метода предельного равновесия, суть которого подробно изложена в учебно-методическом пособии С. М. Скоробогатова [4].
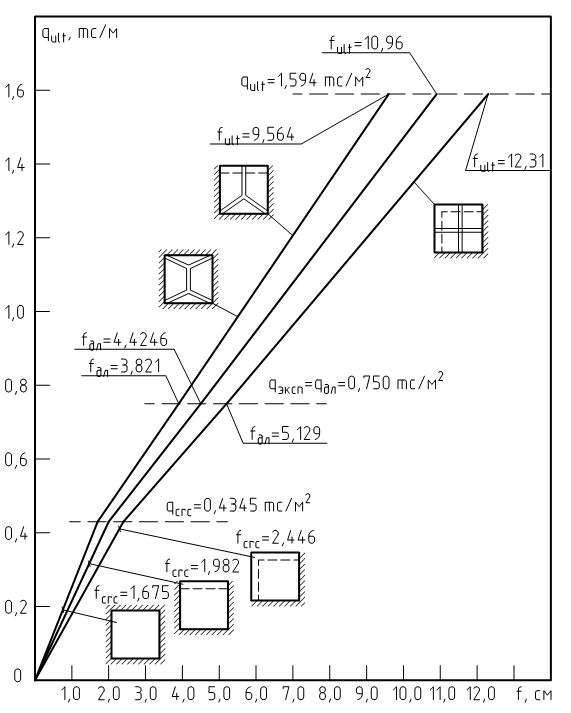
Ввиду сложности задачи для построения методики расчета были использованы результаты давнишних опытов, проведенных в ННИЖБ А.А. Гвоздевым, М.С. Крыловым и др. [5,6]. Опыты показали, что кривая прогибов для удобства может быть аппроксимирована двумя почти прямолинейными участками, у которых скорости нарастания деформаций существенно различаются (см. рис. 1). Первый участок (0 – qcrc) распространяется от начала нагружения до момента образования первых трещин. Второй участок (qcrc – qult) распространяется от момента образования трещин до появления пластических шарниров, т.е. до расчетного предельного состояния (стадия предразрушения).
Приближенно прогиб плит при эксплуатационной нагрузке qэкс = qдл может быть определен по линейной интерполяции между прогибом fcrc, непосредственно предшествующим образованию первых трещин, и прогибом fult, непосредственно предшествующим исчерпанию несущей способности плит:
При этом полностью исчезает необходимость в трудоемком вычислении известного и проблемного коэффициента ψs.
В формуле (1) qэкс = qn – действующая эксплуатационная нормативная равномерно распределенная нагрузка при коэффициенте надежности γf = 1,0. В большинстве случаев qэкс = qдл – длительно действующая нагрузка.
Для шарнирно опертых плит прогиб fcrc определяется как для упругой плиты по формулам строительной механики. Для защемленных по контуру плит определение fcrc встречает дидактические и психологические трудности. За прогиб fcrc следует принимать величины прогиба плит при образовании трещин в пролете (Mcrc = Rbt.nWpl), когда трещины в защемлениях уже имеются. Поэтому формулы строительной механики для определения Mпр не рекомендуются [7].
Дело в том, что опорные моменты Mоп всегда больше, чем Mпр [7]. Увеличение пролетного момента Mпр до величины Mcrc приводит к приращению нагрузки в пролете. Это вызывает увеличение величины опорного момента Mоп = Mcrc +ΔM и в целом увеличение нагрузки q +Δq.
Расчетная схема плиты в данном случае может быть представлена в виде шарнирно опертой плиты, загруженной данной нагрузкой Δq и неизвестными моментами Mоп +ΔM вдоль длинной защемленной стороны (т.е. от q +Δq).
Для определения величин fcrc следует принимать Mоп = Mcrc и пользоваться формулами для упругих плит. От нагрузки Mоп = Mcrc+ΔM (или q +Δq) для схемы с защемлением по контуру:
где q и Δq определяются из формулы:
Для упругих тел обычно пользуются понятием цилиндрической жесткости:
Для железобетона как упруго-пластического тела или тела с трещинами коэффициентом Пуассона не пользуются.
Более того в современных нормах и пособиях рекомендуется использовать специальные формулы для определения величины жесткости D:
В формулах
(5) и (6) пользуются приведенными величинами
![]() ,
особенно при длительном действии нагрузки.
,
особенно при длительном действии нагрузки.
Наибольшую
трудность вызывает определение fult,
которая зависит от кривизны
![]() [7]:
[7]:
Определение прогиба fult встречает методические трудности. В связи с неопределенностью величин опорных моментов в процессе нагружения, после трещинообразования, становится мало определенной величина σs (или Rs,n). Следует сделать следующее замечание, смягчающее остроту проблемы. При малых процентах армирования, что характерно для плитных конструкций, в формуле (7) между величиной (1/r) и Rs,n существует почти прямолинейная зависимость. Поэтому не столь важно, какую величину вместо Rs,n можно использовать.
Однако, несмотря на все преимущества применения метода расчета по предельным состояниям, он представляет серьезную проблему при сочетании с методом конечных элементов, ориентированным на использование сегодняшних программных комплексов.
Современные компьютерные программы расчета строительных конструкций слабо увязывают общие методы решения задач строительной механики с современными нормами, учитывающими новые физико-механические модели. Во многих программах используются линейные зависимости для бетона. В результате нормы проектирования и компьютерные методы развиваются разными путями. В некоторых программах пластические деформации учитываются с помощью единых, малообоснованных, и слишком округленных коэффициентов. Умалчивание о примененных алгоритмах снижает доверие к программным комплексам. Уязвимость безбалочных перекрытий в прогибах из-за малой жесткости не исключает необходимости поверочных расчетов (после расчетов на ЭВМ) по первой и второй группам предельных состояний.
Для устранения этого противоречия необходимо решить задачу получения предельного состояния рассчитываемой конструкции средствами метода конечных элементов. То же возможно только при условии учета всех нелинейных свойств, проявляемых этой конструкцией к моменту достижения ею предельного состояния, т.е. при учете степени влияния и времени появления каждого отдельного нелинейного свойства.
Данная проблема представляется очень актуальной в современных условиях. Одним из возможных способов её решения является метод дополнительных конечных элементов, изложенный в монографии А. В. Ермаковой [8], и сочетающий три метода расчета конструкций: конечных элементов, дополнительных нагрузок и предельных состояний.
Согласно методике этого расчета процесс изменения нелинейных свойств отдельного конечного элемента при постепенном достижении им предельного состояния моделируется при помощи специально разработанных дополнительных конечных элементов, позволяющих менять свойства основного элемента. Предлагаемые дополнительные конечные элементы позволяют строить вектора дополнительных нагрузок независимо от характера наблюдаемых нелинейных свойств основных элементов.
Дополнительные нагрузки могут быть построены тремя способами на основе: дополнительных конечных элементов общего вида, меняющих матрицы жесткости основных элементов; дополнительных элементов первого типа, меняющих напряженное состояние основных элементов, и дополнительных элементов второго типа, меняющих деформированное состояние основных конечных элементов.
Для описания предельного состояния всей конструкции предлагается использовать идеальную модель ее разрушения, представляющую расчетную схему этой конструкции в момент предельного равновесия. Она состоит из двух: расчетной схемы из основных конечных элементов с линейными свойствами и расчетной схемы из дополнительных элементов с нелинейными свойствами, соответствующих данной стадии предельного состояния.
Расчетная схема из дополнительных элементов изменяет исходную схему из линейных элементов таким образом, чтобы она соответствовала достигнутой к данному моменту стадии предельного состояния конструкции; в предельной стадии она превращает исходную расчетную схему в идеальную модель разрушения конструкции.
Из вышесказанного можно сделать вывод, что предлагаемая методика достаточна проста и может служить основой для алгоритмов и программ, реализующих расчет конструкций по предельным состояниям, в том числе и для расчета монолитных железобетонных безбалочных перекрытий с отверстиями.
Литература:
- Скоробогатов С.М., Хомяков В.А., Морданов О.Н., Морданова Е.С. Классификация катастроф железобетонных конструкций // Вестник УрГУПС, 2010, №4. – С. 63-71. ISSN 2079-0392.
- Расчет пластин методами граничной коллокации: монография / Машкин О. В., Рогалевич В. В., - Екатеринбург: Издательство АМБ, 2011. – 76 с.
- Железобетонные плиты с отверстием [Зиновьева Р.В. и др.]. – М.: Стройиздат, 1975. – 112 с.
- Скоробогатов С.М. Поверочные расчеты безбалочных бескапительных монолитных железобетонных перекрытий по второй группе предельных состояний (прогибы, трещины) // Для бакалавров, инженеров и магистрантов специальности ПГС. – Екатеринбург : УрГУПС, – 2011. – 80 с.
- Руководство по расчету статически неопределимых железобетонных конструкций // НИИЖБ. - М.: Стройиздат, 1975. – 193 с.
- Руководство по проектированию железобетонных конструкций с безбалочными перекрытиями – М.: Стройиздат, 1979. – 63 с.
- Проектирование железобетонных конструкций // Справочное пособие [Под ред. А.Б. Голышева]. – Киев, Будiвельник, 1990. – 543 с. (см. главу «Расчет плит», стр. 360-373).
- Ермакова А.В. Метод дополнительных конечных элементов для расчета железобетонных конструкций по предельным состояниям. – М.: АСВ, 2007. – 128 с.