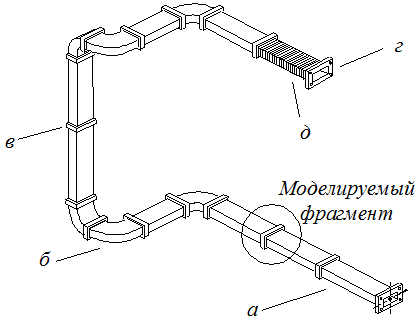
Конструкция волноводно-распределительной системы (ВРС) космических аппаратов (КА) состоит из набора прямых и изогнутых тонкостенных элементов прямоугольного поперечного сечения, соединенных между собой пайкой через муфты в единую конструкцию (рис.1).
Тонкостенные элементы представим как неосесимметричные оболочечные конструкции, которые должны иметь необходимую прочность и жесткость.
Для обеспечения качества и надежности работы ВРС необходимо обеспечить условия ее общей и локальной прочности при всех возможных сочетаниях статических и динамических воздействий на всех этапах ее жизненного цикла.
|
в г д |
а –прямой элемент; б – изогнутый элемент; в – муфта; г – фланец; д – гибкая секция
Рис. 1 Участок волноводно-распределительной системы и его элементы
Для расчета на прочность ВРС и ее участков, состоящих из набора отдельных повторяющихся элементов (рис.1,а-д), необходимо иметь их математические модели, что позволит решать задачи для ВРС любой протяженности и сложности.
Предлагается поэтапное решение данной проблемы. На первом этапе рассмотрим вопрос, каким образом соединять отдельные решения, полученные для каждого элемента волноводно-распределительной системы.
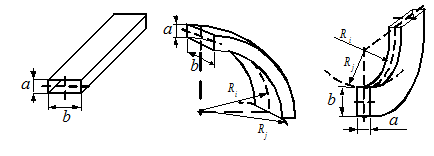
Рассмотрим особенности моделирования наиболее распространенных элементов. Прямой элемент (рис.1,а) представляет собой оболочечную конструкцию, состоящую из отдельных пластинок, радиусы кривизн которых стремятся к бесконечности (R1,2&#;&#;</FONT></I></SPAN>). В углах соединения этих пластин <SPAN LANG="en-US"><I>R</I></SPAN><SUB><I>1</I></SUB><SPAN LANG="en-US"><I><FONT FACE="Symbol">&#;</FONT></I></SPAN><I>0, </I>а <SPAN LANG="en-US">R</SPAN><SUB>2</SUB><SPAN LANG="en-US"><I><FONT FACE="Symbol">&#;</FONT><FONT FACE="Symbol">&#;</FONT></I></SPAN>. Получение решения для такой оболочечной конструкции рассматривается далее на втором этапе моделирования.<P> Прямые элементы необходимо соединять между собой через муфты (рис.1,в) или соединять их с фланцем (рис.1,г), или соединять их с изогнутыми элементами (рис.1,б) или с гибкой секцией (рис.1,д).<P> Изогнутый элемент (рис.1,б) представим совокупностью, соединенных между собой под углом <A HREF="images/3470a4f4.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3470a4f4.gif" NAME="Графический объект4" ALIGN=ABSMIDDLE WIDTH=13 HEIGHT=17 BORDER=0></A> <SPAN LANG="en-US"><I>n</I></SPAN> одинаковых прямых элементов (рис. 2). При <SPAN LANG="en-US"><I>n</I></SPAN><SPAN LANG="en-US"><I><FONT FACE="Symbol">&#;</FONT><FONT FACE="Symbol">&#;</FONT></I></SPAN> будем иметь изогнутый элемент соответствующего радиуса кривизны. <P><BR /> <P><A HREF="images/m3362cf08.png" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m3362cf08.png" NAME="Графический объект5" ALIGN=BOTTOM WIDTH=384 HEIGHT=207 BORDER=0></A><P> Рис. 2 Расчетная схема изогнутого элемента <P><BR /> <P>Следовательно, криволинейный участок представляется разбитым сечениями <SPAN LANG="en-US"><I>i</I></SPAN> на <SPAN LANG="en-US"><I>n</I></SPAN> прямых элементов. На линиях соединения этих прямых элементов, составляющих изогнутый участок, задаются условия перехода, связывающие усилия и перемещения конца <SPAN LANG="en-US"><I>i</I></SPAN><I> – </I>го прямого элемента с усилиями и перемещениями начала (<SPAN LANG="en-US"><I>i</I></SPAN><I>+1) – </I>го прямого элемента.<P> Соединительную муфту (рис.1,в) и фланец (рис.1,г) можно представить в виде рамочной конструкцией, состоящей из четырех, соединенных между собой, балок. Решение этой задачи рассмотрено в [1].<P> При соединении прямого элемента с муфтой или же фланцем будем предполагать, что поперечное сечение муфты в своей плоскости имеет деформации равные нулю, так как жесткость муфты и фланца, по сравнению с жесткостью тонкостенных элементов, соединенных с ними, значительно выше. <P>Если на муфту действуют внешние нагрузки, приведенные к ее нейтральной оси, и представленные в виде вектора <A HREF="images/m1e8ba6cf.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m1e8ba6cf.gif" NAME="Объект3" ALIGN=ABSMIDDLE WIDTH=37 HEIGHT=23></A>, то для совместной работы конструкции ВРС необходимо обеспечить согласование взаимодействия прямых элементов соединенных пайкой с муфтой с двух сторон (рис.3).<P> Со стороны <I>р+1</I>-го прямого элемента на муфту в точке <A HREF="images/m3d5f2d27.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m3d5f2d27.gif" NAME="Объект4" ALIGN=ABSMIDDLE WIDTH=42 HEIGHT=20></A> будет действовать вектор реактивных усилий <A HREF="images/2cfaeed8.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2cfaeed8.gif" NAME="Объект5" ALIGN=ABSMIDDLE WIDTH=53 HEIGHT=23></A>, которые приводятся к нейтральной оси муфты. К вектору внешних нагрузок <A HREF="images/m12e80f04.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m12e80f04.gif" NAME="Объект6" ALIGN=ABSMIDDLE WIDTH=37 HEIGHT=23></A> добавятся реакции <I>р+1</I>-го элемента <A HREF="images/m5b11a725.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5b11a725.gif" NAME="Объект7" ALIGN=ABSMIDDLE WIDTH=125 HEIGHT=23></A>, где <A HREF="images/35b49430.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/35b49430.gif" NAME="Объект8" ALIGN=ABSMIDDLE WIDTH=35 HEIGHT=23></A> - матрица перехода на муфте.<P> Аналогичным образом приведем к нейтральной оси<I> </I>муфты реактивные усилия, действующие со стороны <I>р</I>-го элемента. <P>Уравнение равновесия муфты с учетом этих реакций имеет вид:<P> <A HREF="images/10a3063d.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/10a3063d.gif" NAME="Объект9" ALIGN=ABSMIDDLE WIDTH=185 HEIGHT=26></A>, (1)<P> где <A HREF="images/37acd169.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/37acd169.gif" NAME="Объект10" ALIGN=ABSMIDDLE WIDTH=29 HEIGHT=20></A>- вектор перемещений; <A HREF="images/990f779.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/990f779.gif" NAME="Объект11" ALIGN=ABSMIDDLE WIDTH=30 HEIGHT=19></A> - матрица жесткости муфты.<P> <A HREF="images/13cdcba5.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/13cdcba5.gif" NAME="Объект12" ALIGN=BOTTOM WIDTH=368 HEIGHT=171></A><P> Рис. 3 Схема моделирования фрагмента совместной работы <P>соединяемых пайкой прямых элементов и муфты<P> <BR /> <P>Данное уравнение необходимо дополнить условиями неразрывности перемещений муфты и связанных с ней тонкостенных элементов. Приводя, также как и для реактивных усилий, перемещения точек контакта (<SPAN LANG="en-US"><I>S</I></SPAN><SUP><I>р+1</I></SUP><I> </I>и<I> </I><SPAN LANG="en-US"><I>S</I></SPAN><SUP><I>р</I></SUP>) тонкостенных элементов с муфтой к ее нейтральной оси, получим:<P> <A HREF="images/m3b96bcb.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m3b96bcb.gif" NAME="Объект13" ALIGN=ABSMIDDLE WIDTH=193 HEIGHT=26></A>. (2)<P> где <A HREF="images/3d222a15.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3d222a15.gif" NAME="Объект14" ALIGN=ABSMIDDLE WIDTH=72 HEIGHT=23></A> - вектора перемещений точек <SPAN LANG="en-US"><I>S</I></SPAN><SUP><I>р+1</I></SUP><I> </I>и<I> </I><SPAN LANG="en-US"><I>S</I></SPAN><SUP><I>р</I></SUP>; <A HREF="images/111d8007.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/111d8007.gif" NAME="Объект15" ALIGN=ABSMIDDLE WIDTH=43 HEIGHT=23></A>- матрицы перехода.<P> Полное условие перехода через муфту дополнительно должно содержать геометрические условия перехода деформаций и усилий, зависящие от угла между соответствующими сечениями. А полный вектор <A HREF="images/m7b62ee56.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m7b62ee56.gif" NAME="Объект16" ALIGN=ABSMIDDLE WIDTH=24 HEIGHT=20></A> перехода будет иметь вид: <P><A HREF="images/4a052d97.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/4a052d97.gif" NAME="Графический объект6" ALIGN=ABSMIDDLE WIDTH=275 HEIGHT=27 BORDER=0></A> <A HREF="images/7b54673a.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/7b54673a.gif" NAME="Объект17" ALIGN=ABSMIDDLE WIDTH=91 HEIGHT=20></A>.<P> На втором этапе рассмотрим прямого тонкостенного элемента, который является основой моделирования всей волноводно-распределительной системы.<P> Прямой тонкостенный элемент волноводно-распределительной системы (рис. 4,а) космического аппарата можно представить в виде оболочечной конструкции, состоящей из отдельных пластинок, радиусы кривизн которых стремятся к бесконечности (<SPAN LANG="en-US"><I>R</I></SPAN><SUB><I>1,2</I></SUB><SPAN LANG="en-US"><I><FONT FACE="Symbol">&#;</FONT><FONT FACE="Symbol">&#;</FONT></I></SPAN>). В углах соединения этих пластин <SPAN LANG="en-US"><I>R</I></SPAN><SUB><I>1</I></SUB><SPAN LANG="en-US"><I><FONT FACE="Symbol">&#;</FONT></I></SPAN><I>0, </I>а <SPAN LANG="en-US">R</SPAN><SUB>2</SUB><SPAN LANG="en-US"><I><FONT FACE="Symbol">&#;</FONT><FONT FACE="Symbol">&#;</FONT></I></SPAN>. Но эти условия не позволяют использовать расчетные методы и уравнения существующей теории оболочек [2].<P> Выходом из данной ситуации будет представление прямого элемента в виде составной конструкции, состоящей из набора пластин, расположенных под прямым углом друг к другу (рис. 4,б). <P><A HREF="images/64f5d750.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/64f5d750.gif" NAME="Объект18" ALIGN=BOTTOM WIDTH=618 HEIGHT=313></A><P> Рис. 4 Расчетная схема оболочечной конструкции из отдельных пластин<P> <BR /> <P>Рассматривая отдельную тонкую пластинку в ее локальной системе координат <A HREF="images/m660aa63b.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m660aa63b.gif" NAME="Объект19" ALIGN=ABSMIDDLE WIDTH=59 HEIGHT=18></A>, воспользуемся геометрически линейными уравнениями [2], которые с учетом параметров Ламе <SPAN LANG="en-US"><I>A</I></SPAN><I> = </I><SPAN LANG="en-US"><I>B</I></SPAN><I> = 1</I>, радиусы кривизны <SPAN LANG="en-US"><I>R</I></SPAN><SUB><I>1</I></SUB><I>=</I><SPAN LANG="en-US"><I>R</I></SPAN><SUB><I>2</I></SUB><I>=</I><I><FONT FACE="Symbol">&#;</FONT></I><I> </I>при<I> </I>толщине пластины <SPAN LANG="en-US"><I>h</I></SPAN><I>,</I> примут вид:<P> <A HREF="images/m20b9339e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m20b9339e.gif" NAME="Объект20" ALIGN=ABSMIDDLE WIDTH=585 HEIGHT=94></A> (3)<P> Первые два уравнения в системе (3) совместно с уравнением совместности деформаций описывают плоскую задачу. Подставив вместо усилий <SPAN LANG="en-US"><I>N</I></SPAN><SUB><I>1</I></SUB><I>, </I><SPAN LANG="en-US"><I>N</I></SPAN><SUB><I>2</I></SUB><I>, </I><SPAN LANG="en-US"><I>S</I></SPAN> их выражения в функциях напряжений <A HREF="images/7dc6b662.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/7dc6b662.gif" NAME="Объект21" ALIGN=ABSMIDDLE WIDTH=79 HEIGHT=20></A>:<P> <A HREF="images/6b0f2e4f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6b0f2e4f.gif" NAME="Объект22" ALIGN=ABSMIDDLE WIDTH=85 HEIGHT=43></A>; <A HREF="images/7bc40e4f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/7bc40e4f.gif" NAME="Объект23" ALIGN=ABSMIDDLE WIDTH=87 HEIGHT=43></A>; <A HREF="images/m6bec147a.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m6bec147a.gif" NAME="Объект24" ALIGN=ABSMIDDLE WIDTH=104 HEIGHT=40></A>. (4)<P> получим дифференциальное уравнение 4-го порядка для <SPAN LANG="en-US"><I>i</I></SPAN>-й пластины в виде:<P> <A HREF="images/1efb0881.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/1efb0881.gif" NAME="Графический объект7" ALIGN=ABSMIDDLE WIDTH=366 HEIGHT=59 BORDER=0></A>. (5)<P> Последние три уравнения (3) описывают изгиб пластины. С учетом прогиба пластины <A HREF="images/33fc2a92.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/33fc2a92.gif" NAME="Объект25" ALIGN=ABSMIDDLE WIDTH=84 HEIGHT=20></A>, выражения для изгибающих и крутящих моментов <SPAN LANG="en-US"><I>M</I></SPAN><SUB><I>1</I></SUB><I>, М</I><SUB><I>2</I></SUB><I>, Н </I>будут иметь вид:<P> <A HREF="images/b38d1d0.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/b38d1d0.gif" NAME="Графический объект8" ALIGN=ABSMIDDLE WIDTH=160 HEIGHT=51 BORDER=0></A>;<A HREF="images/3ba85e3c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/3ba85e3c.gif" NAME="Графический объект9" ALIGN=ABSMIDDLE WIDTH=162 HEIGHT=51 BORDER=0></A>; <A HREF="images/m46a21013.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m46a21013.gif" NAME="Графический объект10" ALIGN=ABSMIDDLE WIDTH=144 HEIGHT=49 BORDER=0></A>. (6)<P> где <SPAN LANG="en-US"><I>D</I></SPAN> - цилиндрическая жесткость пластины; <I><FONT FACE="Symbol">&#;</FONT></I>- коэффициент Пуассона.<P> Подставив (6) в соответствующие уравнения системы 3) и произведя преобразования получим дифференциальное уравнение изгиба 4-го порядка <SPAN LANG="en-US"><I>i</I></SPAN>-й пластины в виде:<P> <A HREF="images/60ccf3bf.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/60ccf3bf.gif" NAME="Графический объект11" ALIGN=ABSMIDDLE WIDTH=548 HEIGHT=51 BORDER=0></A> (7)<P> Уравнения (5) и (7) являются взаимосвязанными, и их совместное решение определяет полное напряженно-деформированное состояние (НДС) каждой <SPAN LANG="en-US"><I>i</I></SPAN>-й пластины. Эти уравнения учитывают взаимосвязь всех внутренних силовых и деформационных факторов в пластине для общего случая нагружения, что оказывает существенное влияние на точность решения этой задачи применительно к тонкостенным конструкциям. <P><B>Полученная система дифференциальных уравнений (6) и (7), без последних трех слагаемых в уравнении (7), подобна уравнениям, полученным С.П. Тимошенко, для которых, как им и указано в [3] на с.463, общее решение не получено. Эта проблема является не решенной в аналитическом виде до сих пор даже для одной пластинки.</B><P> В нашем случае для прямого элемента, составленного из четырех пластин, уравнения (6) и (7) можно свести к соответствующей подсистеме дифференциальных уравнений. <P>Условия эксплуатации волноводно-распределительной системы для космических аппаратов предполагают наличие как статических, так и динамических нагрузок. Следовательно, в дифференциальном уравнении (7), в правой его части, появится еще одно слагаемое <A HREF="images/m18f06418.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m18f06418.gif" NAME="Объект26" ALIGN=ABSMIDDLE WIDTH=78 HEIGHT=46></A>. С учетом этого, полная система дифференциальных уравнений, описывающая статическое и динамическое состояния прямого элемента волноводно-распределительной системы космического аппарата, будет иметь вид (8).<P> <A HREF="images/m6a7d4508.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m6a7d4508.gif" NAME="Объект27" ALIGN=ABSMIDDLE WIDTH=676 HEIGHT=746></A> (8)<P> В полученной системе выделены четыре подсистемы, каждая из которых описывает НДС соответствующей пластины, которые связаны между собой граничными условиями при соединении их между собой (рис.4).<P> Полученная система дифференциальных уравнений (8) является значительно более сложной, чем система дифференциальных уравнений, полученная С.П. Тимошенко в [3]. Нами в имеющейся математической литературе не обнаружено информации о решении подобного вида систем дифференциальных уравнений.<P> Имеются частные случаи приближенного решения только лишь одной подсистемы, в которой отсутствует динамический член и с определенными граничными условиями. Но в то же время, не указывается, какой точности получаются результаты и не обсуждается их достоверность.<P> Известные методы конечно-элементных решений данной задачи дают различные результаты и очень большие погрешности, особенно в динамической постановке и при минимальной толщине стенки прямого элемента волноводно-распределительной системы космического аппарата. <P><BR /> <P>Литература: <OL><LI><P> Сильченко П. Н. Напряженно-деформированное состояние паяных волноводно-распределительных систем космических аппаратов связи / П. Н. Сильченко, И. В. Кудрявцев, М. М. Михнев // Технология машиностроения. – 2006. – № 9. – С. 53-57.<LI><P> Новожилов В.В. Линейная теория тонких оболочек /В.В. Новожилов, К.Ф. Черных, Е.И. Михайловский. – Л.: Политехника, 1991. – 656 с<LI><P> Тимошенко С.П. Пластинки и оболочки./ С.П. Тимошенко, С. Войновский-Кригер – М.: Эдиториал УРСС, пер. с англ. изд.3, 2009.– 640 с.<LI><P> Мяченков В. И., Мальцев В. П. Методы и алгоритмы расчета пространственных конструкций на ЭВМ ЕС. – М.: Машиностроение, 1984.– 280 с.<LI><P> Погорелов В. Строительная механика тонкостенных конструкций. –М.: Эдиториал УРСС, 2008. – 528 с.</OL>