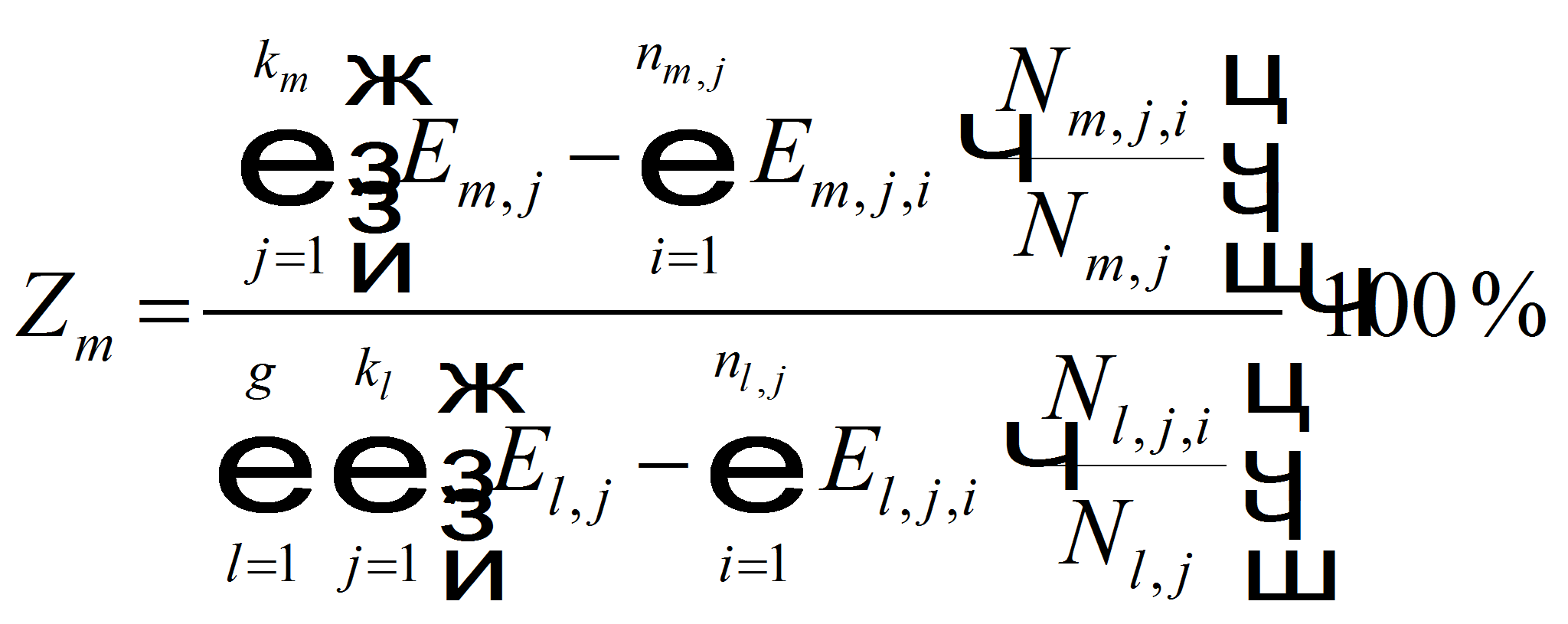Рассмотрен один из подходов к решению задач автоматического исследования данных – деревья решений; введено понятие значимости входных атрибутов и формула ее расчета; приведены результаты практического применения этого метода в задаче выявления значимых факторов для прогнозирования электропотребления металлургическим предприятием.
Ключевые слова. Деревья решений; значимость; входные атрибуты модели; электропотребление; металлургия.
Проблема прогнозирования электропотребления предприятием металлургического профиля представляет собой сложную многопараметрическую задачу, имеющую вероятностную составляющую [6, с.117]. Объём фактического использования электроэнергии обусловлен не только управленческими решениями, структурой портфеля заказов промышленного предприятия, но и типом дня (рабочий день или выходной), погодными условиями, временем суток и многими другими факторами. Причинная связь электропотребления с каждым из этих параметров довольно сложна и не имеет однозначного формального описания линейной моделью. В то же время применение нелинейных регрессионных моделей проблематично. Для этого требуется явное задание характера нелинейности еще до проведения анализа, что является серьезным ограничением [5, с.41].
Таким образом, учитывая специфичность и сложность задачи, можно сделать вывод от том, что хорошо зарекомендовавшие себя в случае с регрессионной моделью методы1 отбора значимых входных признаков не могут быть применены [1, с. 345].
Одним из наиболее перспективных подходов к решению задач автоматического исследования данных, лишенному рассмотренных выше недостатков, является дерево решений – способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение [2, с.94]. Под правилом понимается логическая конструкция, представленная в виде "если ... то ...".
На сегодняшний день существует значительное число алгоритмов, реализующих деревья решений: CART, C4.5, NewId, ITrule, CHAID, CN2 и др. [3, с.29].
Большинство из известных алгоритмов являются "жадными алгоритмами". Если один раз был выбран атрибут, и по нему было произведено разбиение на подмножества, то алгоритм «не может» вернуться назад и выбрать другой атрибут, который дал бы лучшее разбиение. Поэтому на этапе построения нельзя сказать даст ли выбранный атрибут, в конечном итоге, оптимальное разбиение [3, с.72].
В работе за основу взят алгоритм C4.52 построения дерева решений, для которого количество потомков у узла не ограничено, решающий только задачи классификации, так как «не умеет» работать с непрерывным целевым полем [2, с.308].
Для решения поставленной задачи необходимо, во-первых, внести изменения в процедуру разбиения по значениям непрерывного типа; во-вторых, что самое главное, ввести понятие «значимости» входных атрибутов и определить формулу для её расчетов.
Ниже приведён алгоритм разбиения по значениям непрерывного типа :
- Упорядочить все значения по возрастанию.
-
Разбить исходное множество
 на
два -
на
два -
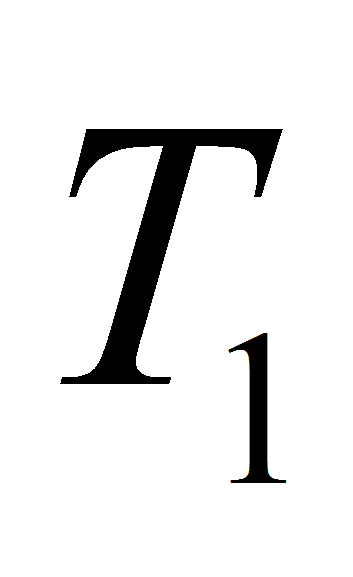 и
и
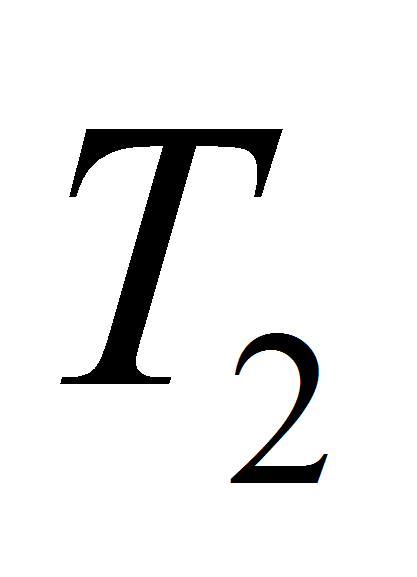 .
На первой итерации в
.
На первой итерации в
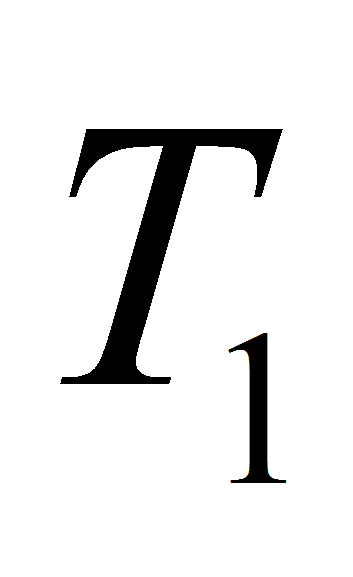 попадает только первый элемент, остальные – в
попадает только первый элемент, остальные – в
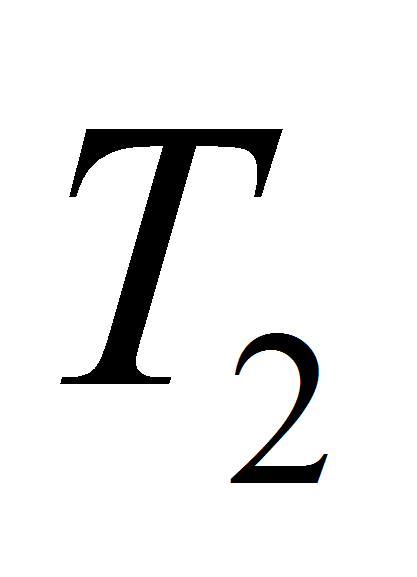 .
На следующей итерации первый элемент из
.
На следующей итерации первый элемент из
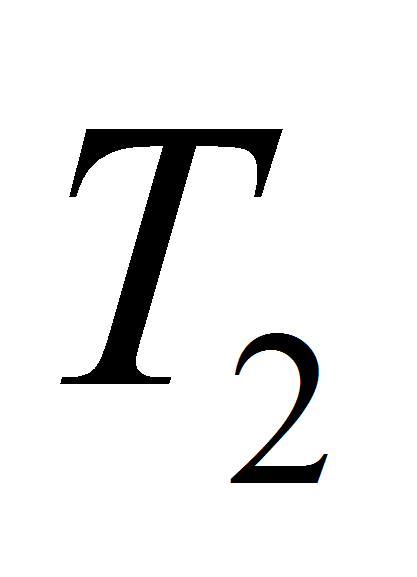 по падает в
по падает в
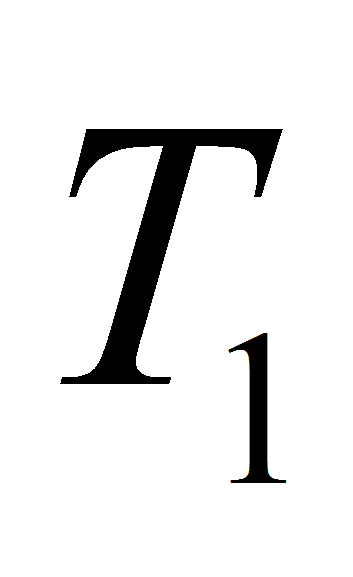 и т.д.
и т.д. -
Вычислить индекс
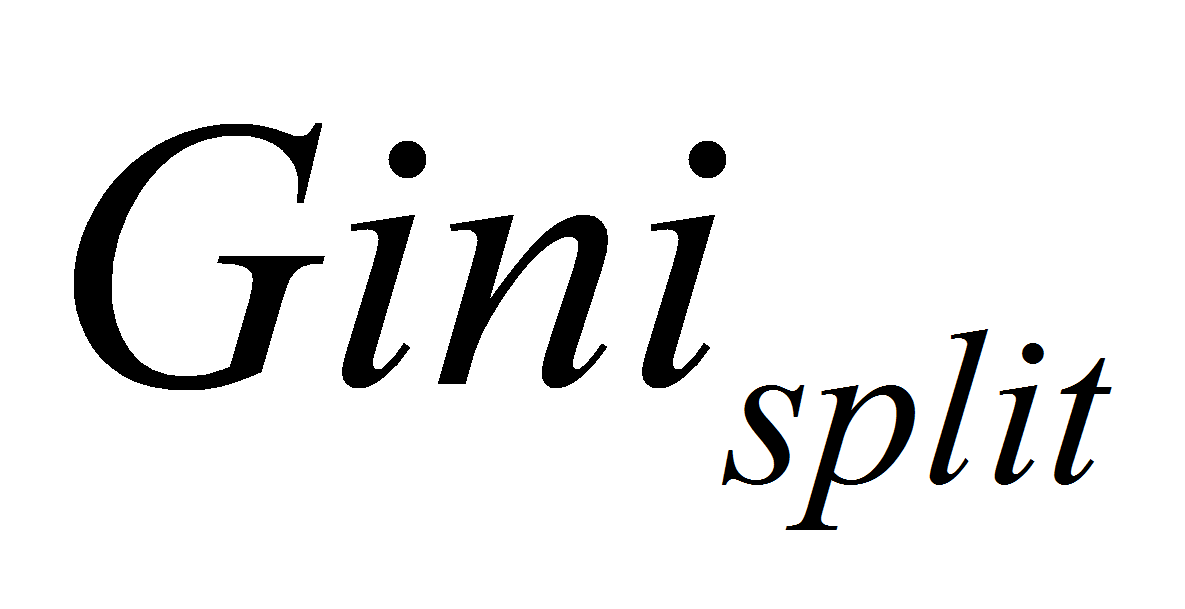 для каждого из разбиений множества
для каждого из разбиений множества
 .
Выбрать то разбиение, для которого индекс
.
Выбрать то разбиение, для которого индекс
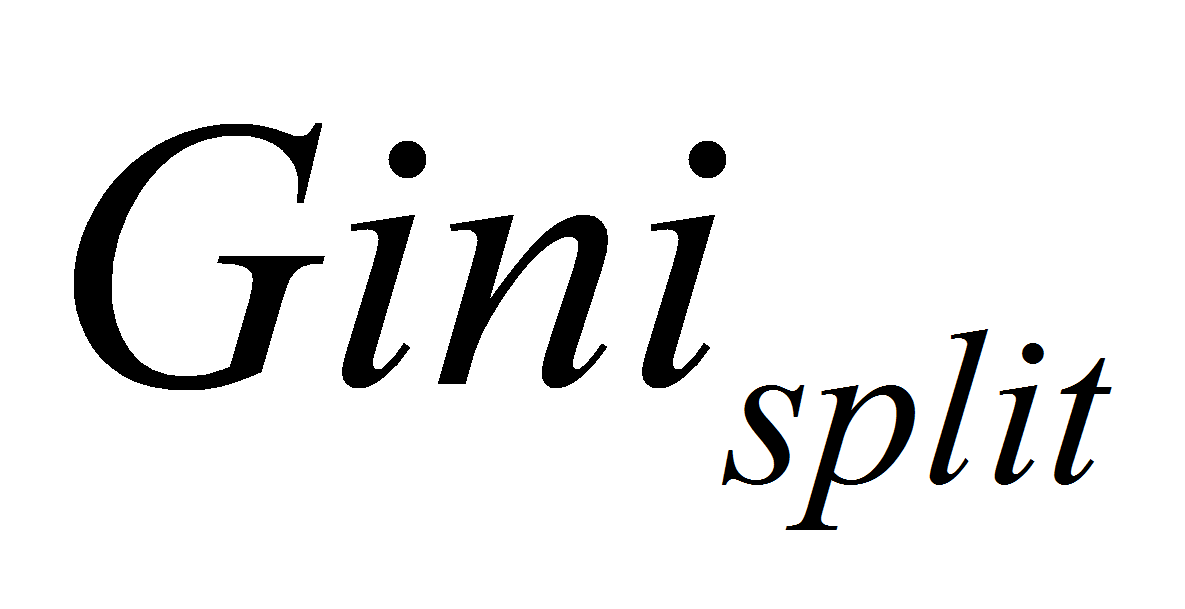 минимален. Используются следующие соотношения:
минимален. Используются следующие соотношения:
- Дальнейшее разбиения узла прекращается при выполнении одного из условий:
- в узле содержится достаточное количество примеров (настроечный параметр);
- узел содержит примеры одного класса;
- количество нераспознанных примеров меньше минимального количества примеров в узле (настроечный параметр).
Теперь введем понятие «значимости» входного атрибута. Под значимостью атрибута будем понимать показатель, характеризующий, насколько сильно выходное поле зависит от данного входного.
Формула для расчета значимости имеет вид:
где
![]() -
количество входных атрибутов,
-
количество входных атрибутов,
![]() -
количество узлов, которые были разбиты по атрибуту
-
количество узлов, которые были разбиты по атрибуту
![]() ,
,
![]() -
энтропия родительского узла, разбитого по атрибуту
-
энтропия родительского узла, разбитого по атрибуту
![]() ,
,
![]() -
энтропия дочернего узла для
-
энтропия дочернего узла для
![]() -го,
разбитого по атрибуту
-го,
разбитого по атрибуту
![]() ,
,
![]() ,
,
![]() -
количество примеров в соответствующих узлах,
-
количество примеров в соответствующих узлах,
![]() -
количество дочерних узлов для
-
количество дочерних узлов для
![]() -го
родительского.
-го
родительского.
Вычисление показателя значимости для атрибутов возможно только после построения дерева классификационных правил.
Технологические процессы потребления электроэнергии подчиняются циклическим, функциональным и случайным тенденциям, из которых наиболее прогнозируемые циклические зависимости (как правило, суточные, недельные и годичные).
Циклические зависимости составляют 70 – 80 % всех отклонений в процессе потребления электроэнергии [6, с.46]. Наиболее существенными циклическими факторами практически во всех производственных процессах являются: величины фактического потребления электроэнергии в предыдущие периоды, время суток, день недели, долгота светового дня.
Закономерности функционального характера являются вторым из основных изучаемых факторов при прогнозировании, их долевое участие составляет приблизительно 10 – 15 % от всего объема отклонений. В эту группу включаются отклонения, объясняемые известными и относительно предсказуемыми факторами производства: температурой воздуха или теплоносителя, значениями и прогнозами параметров, являющихся основными производственными факторами, определившими профиль и величины фактического потребления электроэнергии (объем поставок сырья, объем самого производства) и т.д.
И, наконец, случайные тенденции составляют третью, завершающую компоненту прогноза: их долевое участие в общем процессе невелико, но амплитуда отклонений может быть довольно значительна. Очевидно, что назвать такие отклонения «истинно случайными» будет неверно: каждое отклонение может быть впоследствии объяснено вполне закономерными причинами.
Дерево решений, построенное на основе исходных данных потребления электроэнергии одним из крупных предприятий металлургического профиля, получилось сильноветвистым. На рисунке 1 приведена лишь одна его ветвь (значения всех параметров указаны в условных единицах измерения).
Дальнейшие вычисления показали, что основными факторами, определяющими достоверность прогноза, являются следующие (табл. 1).
Таблица 1
Значимость основных факторов для прогнозной величины электропотребления в задаче суточного прогнозирования
|
№ параметра |
Параметр |
Значимость, % |
|
1 |
Потребление электроэнергии в предыдущий день |
47 |
|
2 |
Объём производства в предыдущий день |
18 |
|
3 |
Потребление электроэнергии два дня назад |
13 |
|
4 |
Статус дня |
12 |
|
5 |
Среднесуточная температура воздуха |
7 |
|
6 |
Долгота дня |
3 |
Рис. 1. Ветвь дерева решений в задаче прогноза электропотребления металлургическим предприятием
В задачах краткосрочного прогнозирования электропотребления распределение значимости параметров, а возможно и их состав, будет иным.
Таким образом, для целевого метода прогнозирования основными влияющими факторами являются автокорреляционные: потребление электроэнергии в предыдущий день и два дня назад, а также статус дня и объем производства в предыдущий день.
Из выбранных основных входных данных наименьшей точностью обладает статус дня: все возможные состояния описываются набором всего из 5-ти значений: рабочий день, рабочий день по 6-ти дневной неделе, рабочий день по приказу руководителя предприятия, выходной день, праздничный день. В сочетании с достаточно высокой степенью значимости этого параметра ошибка в его значении может привести к принципиально неверному прогнозу. Поэтому следует отметить, что улучшение качества метода прогнозирования в первую очередь должно быть направлено на введение в модель дополнительных данных, таких как графики работы подразделений, объемы выпуска по цехам и прочее. Однако, дублирование информации в составе избыточного признака не просто не улучшает качество модели, но и порой, наоборот, ухудшает его.
К примеру, при добавлении к существующему набору входных параметров группы энергоресурсов, сопутствующих электроэнергии в металлургическом производстве, наблюдалось ухудшение основных показателей качества прогнозирования. К этой группе относятся следующие показатели: кислород технологический, азот компримированный, сжатый воздух, вода техническая оборотная и т.д.
Детальный анализ ситуации выявил мультиколлинеарность между этими параметрами и электропотреблением. В доказательство сказанного, исследуем увеличение стоимости кислорода технологического. Как видно из рис. 2, основную долю (21 % из 24 %) в увеличении стоимости занимают энергозатраты – в большей степени электроэнергия. Аналогичная ситуация имеет место и по другим параметрам указанной группы.
Р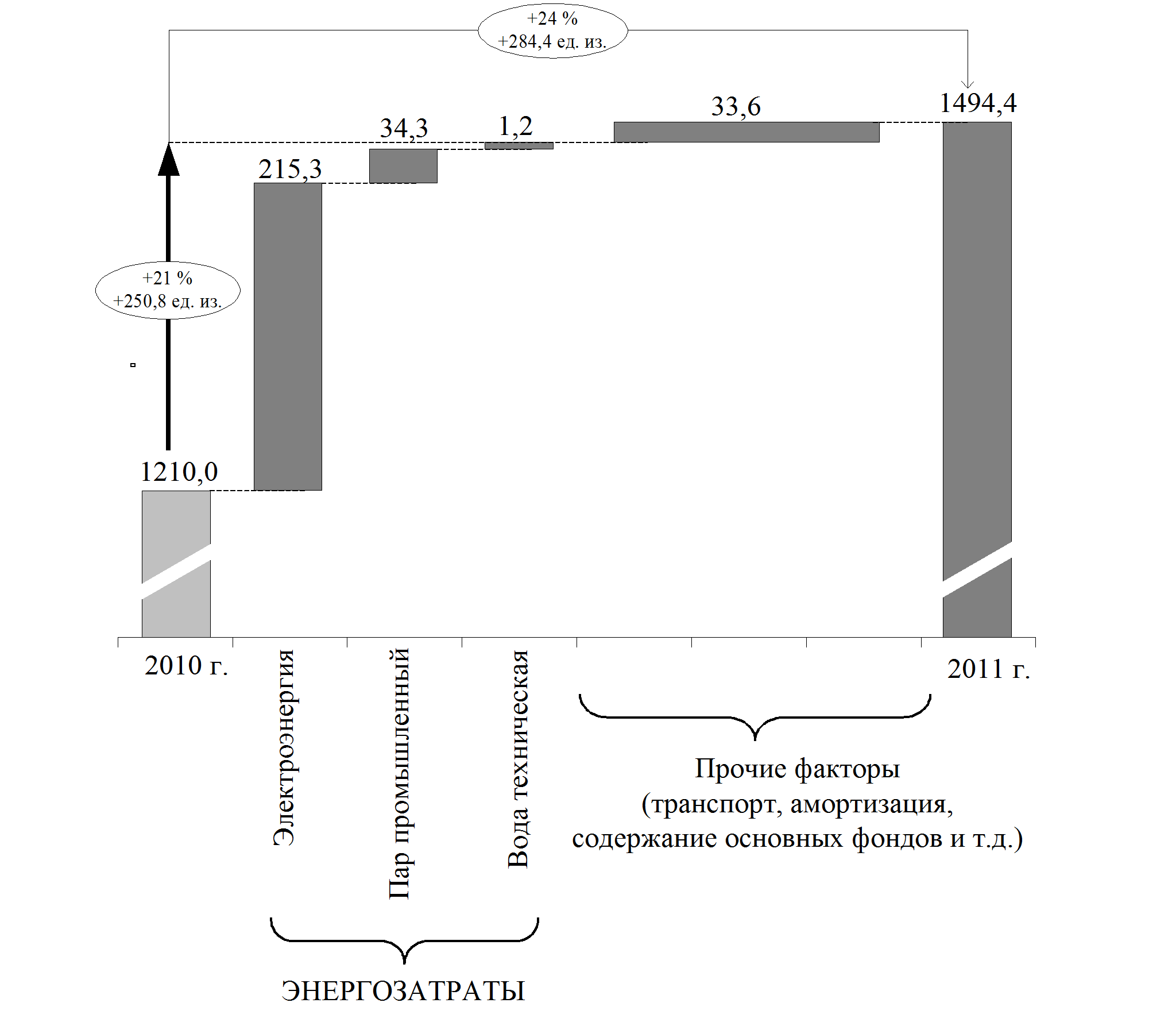 ис.
2. Увеличение стоимости кислорода технологического в 2011 году к 2010
году
ис.
2. Увеличение стоимости кислорода технологического в 2011 году к 2010
году
(в условных единицах измерения)
Проведенный выше анализ применимости деревьев принятия решений для задачи отбора значимых параметров для прогнозирования объёмов потребления электроэнергии показал, что данный метод применим для решения таких задач в рамках крупных потребителей электроэнергии, работающих в секторе свободной торговли. Изложенный подход не претендует на полную замену высококвалифицированного труда эксперта-энергетика предприятия. Однако, используя средства и методы по детальной обработке и всестороннему анализу больших массивов данных, эксперт предприятия может выйти на качественно иной уровень прогнозирования, своевременно реагируя на изменения в структуре суточного энергопотребления с помощью инструмента для составления более точных заявок на длительный срок – неделя, месяц.
Литература:
- Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики, М.: Юнити, 1998. С.1005
- Коршунов Ю.М. Математические основы кибернетики. М.: Энергоатомиздат, 1987. С.496
- Ларичев О.И., Мошкович Е.М. Качественные методы принятия решений. Вербальный анализ решений. М.: Наука. Физматлит, 1996. С.208
- Левитин А.В. Алгоритмы: введение в разработку и анализ, М.: Вильямс, 2006. С. 576
- Никифоров Г.В., Олейников В.К., Заславец Б.И. Энергосбережение и управление электропотреблением в металлургическом производстве. М.: Энергоатомиздат, 2003. C. 480.
- Цымбал В.П. Математическое моделирование металлургических процессов. М.:Металлургия, 1986. С.239
1 процедура Forward Selection (прямой отбор), процедура Backward Elimination (обратное исключение), процедура Stepwise, процедура Best Subsets (лучшие подмножества)
2 C4.5 – алгоритм построения дерева решений, количество потомков у узла не ограничено. Не умеет работать с непрерывным целевым полем, поэтому решает только задачи классификации.