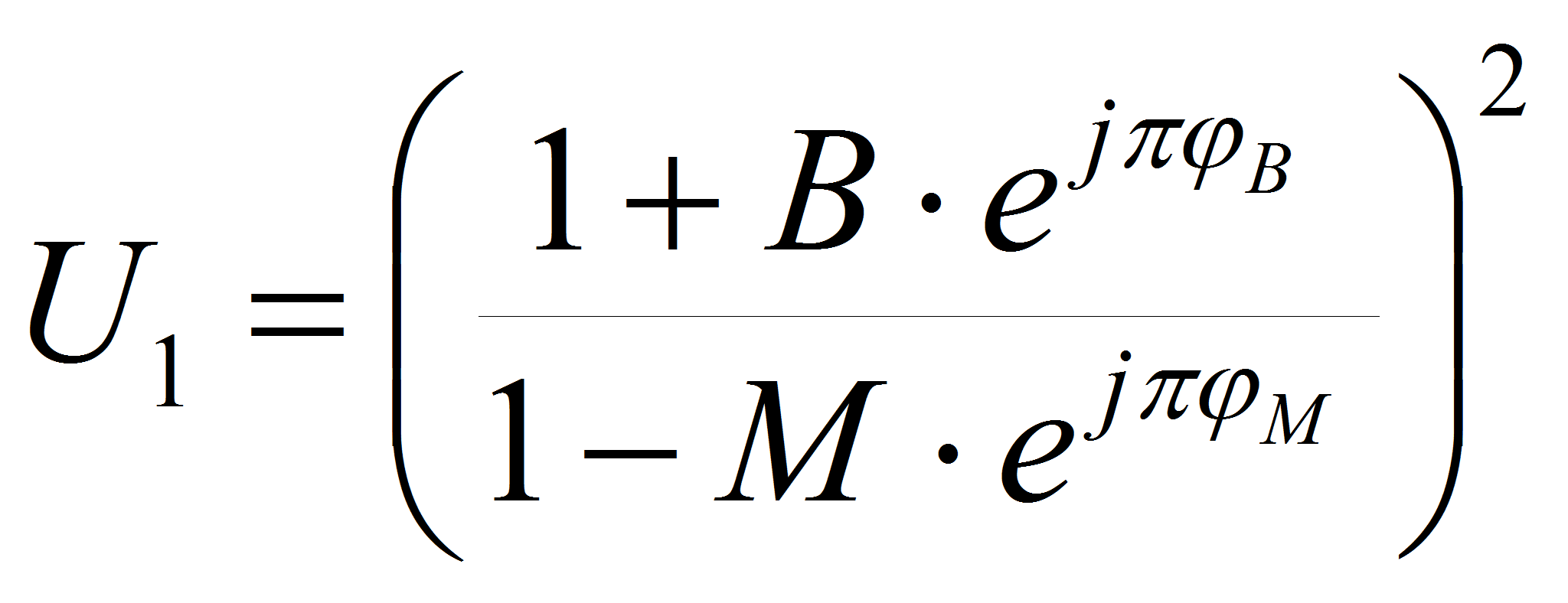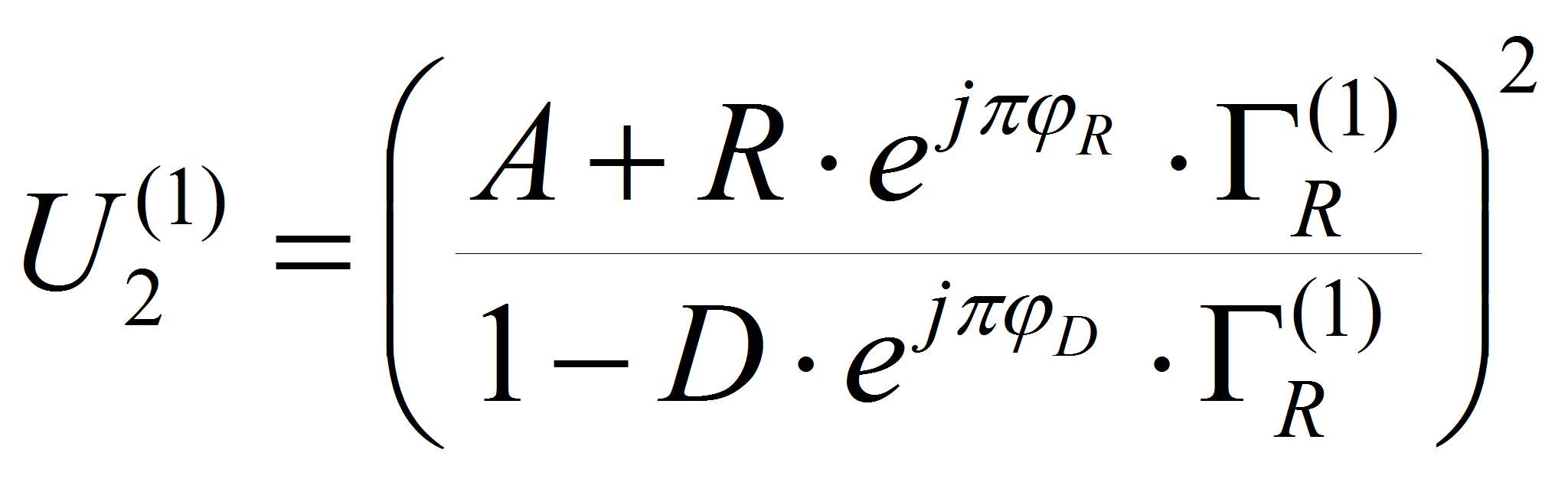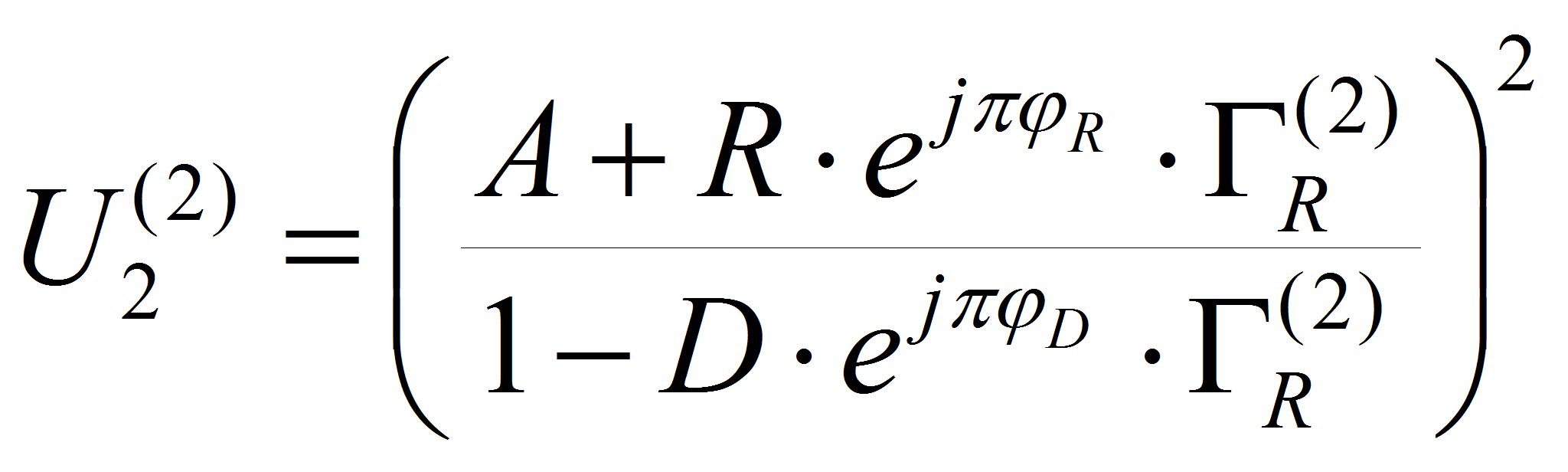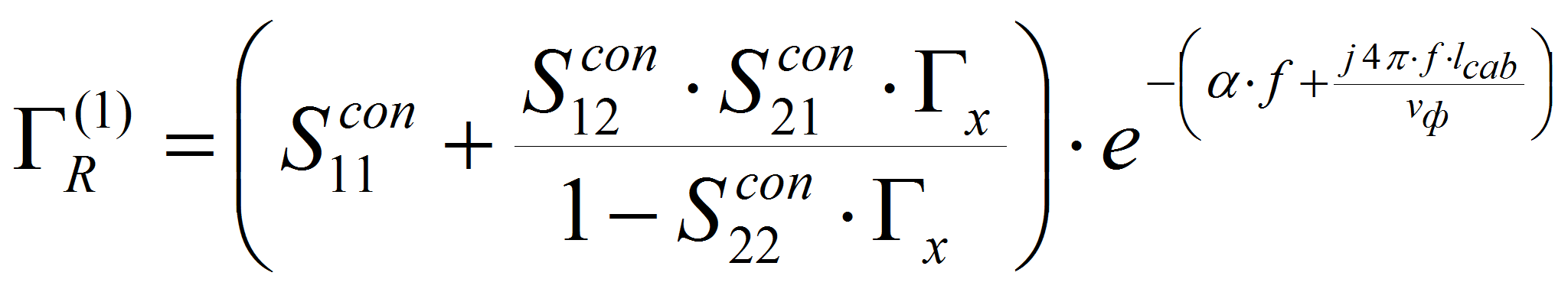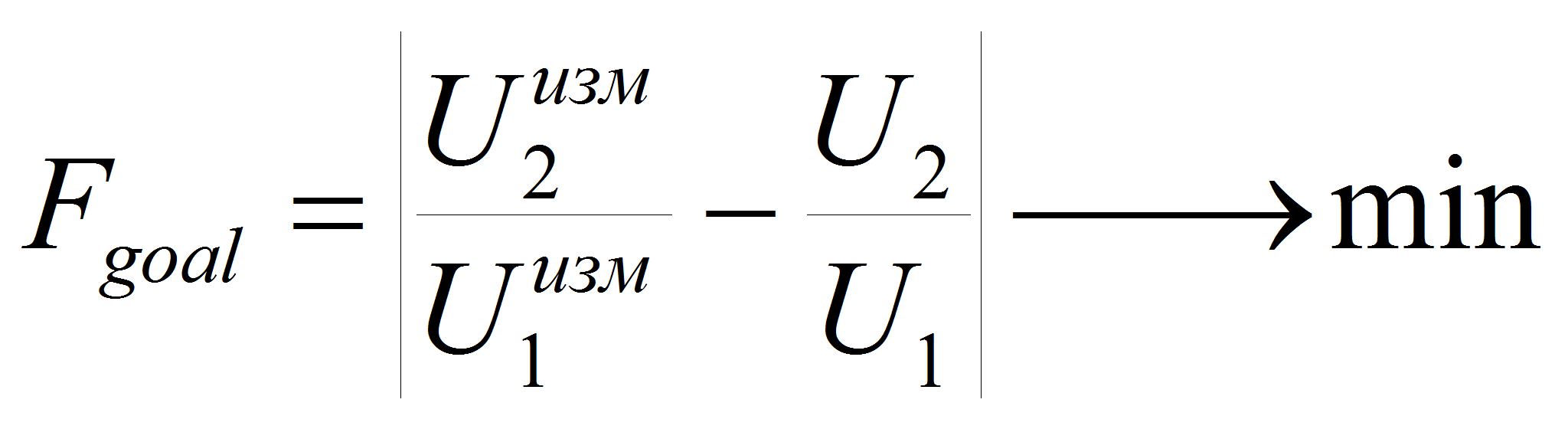Для измерения параметров устройств и электронных компонентов в диапазоне СВЧ широко используются векторные анализаторы электрических цепей. Однако их высокая стоимость обусловливает интерес к новым измерителям, одними из которых являются интеллектуальные измерительные системы, в которых информационные сигналы детекторов подвергаются сложной обработке, а измеряемые параметры представляются моделями в виде функциональных рядов [1]. Расширение динамического диапазона и снижение стоимости измерительной системы реализуется различными режимами детектирования информационных сигналов (амплитудного, гомодинного) и различными режимами возбуждения тестируемого устройства. При гомодинном детектировании информационных сигналов используется низкочастотная модуляция зондирующего испытуемый объект (например, резистивный компонент) сигнала генератора СВЧ [2]. При амплитудном детектировании модулированных сигналов также повышается точность измерений ввиду отсутствия необходимости применения усилителей постоянного тока, обусловливающих дополнительную погрешность дрейфа нуля. При сочетании с анализатором спектра возможно расширение функциональности системы [3].
Применяемые в технике СВЧ резистивные компоненты, как правило, имеют сопротивление 50 Ом, либо кратные и дольные значения в нешироком диапазоне. Резистивные СВЧ-компоненты используются как в согласованном, так и рассогласованном режимах, поэтому требуется обеспечивать широкий динамический диапазон измерений.
Представляемый способ отличается от известных тем, что модулированным является только один из информационных сигналов, а не зондирующий. Измерительный преобразователь содержит управляемый переключатель, попеременно коммутирующий встроенную в него нагрузку с неизвестным коэффициентом отражения и подключаемую тестируемую нагрузку. Модуляция информационных сигналов обусловлена различием модулей коэффициентов отражения от тестируемой и встроенной нагрузок.
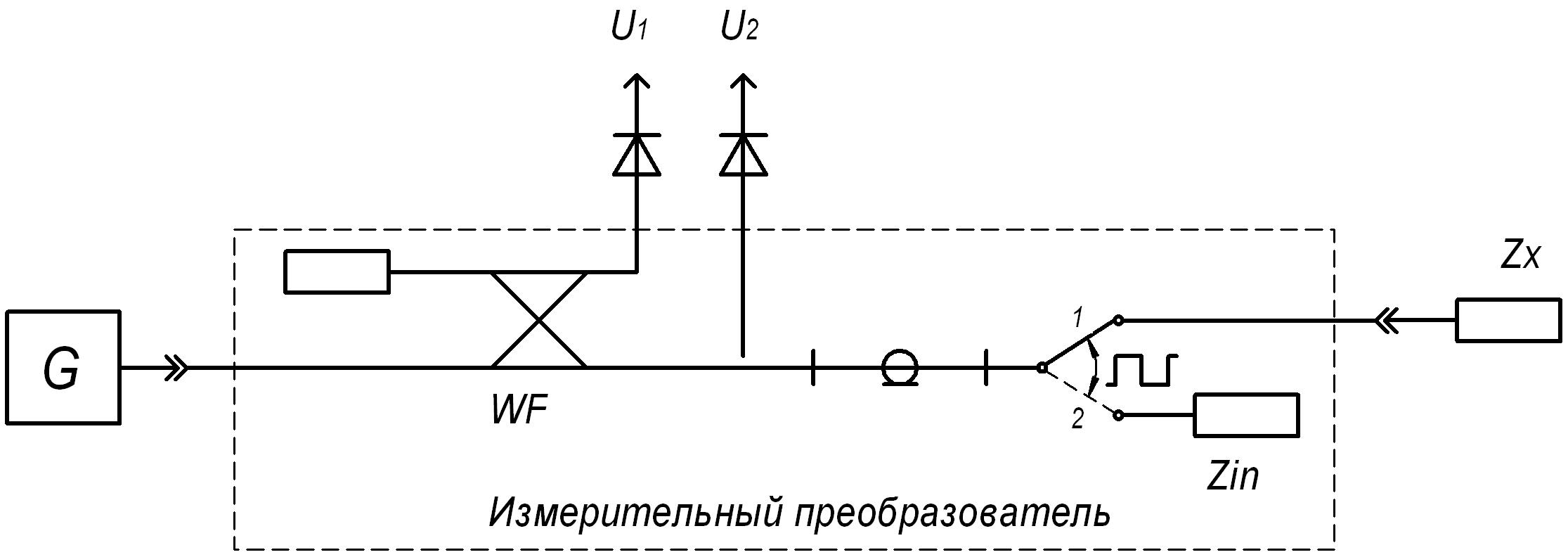
На рисунке 1 приведена схема измерения. Сигнал генератора качающейся частоты G подается на вход измерительного преобразователя. Часть сигнала через направленный ответвитель WF поступает на вход первого детектора (информационный сигнал U1, пропорциональный амплитуде падающей волны). После направленного ответвителя сигнал через зонд подается на вход второго детектора (информационный сигнал U2) и отрезок коаксиального кабеля, выход которого подключен к входу управляемого переключателя, коммутирующего встроенную нагрузку Zin и выход измерительного преобразователя, к которому подключенная тестируемая нагрузка (резистивный компонент) Zx. Переключатель управляется низкочастотной последовательностью прямоугольных импульсов.
|
Рисунок 1 – Схема измерения с коммутацией встроенной нагрузки |
Информационные сигналы используются для идентификации параметров моделей измерительного преобразователя и тестируемой нагрузки (резистивного компонента).
Выходные сигналы квадратичных детекторов определяются выражениями (сигналы второго детектора при верхнем и нижнем положениях переключателя обозначены верхними индексами 1 и 2 соответственно):
|
|
(1) |
где B, M, R, D, φB, φM, φR, φD – параметры модели измерительного преобразователя, определяемые при проведении калибровочных измерений;
![]() и
и
![]() –
коэффициенты отражения на входе встроенного коаксиального кабеля при
верхнем и нижнем по схеме положениях переключателя соответственно.
–
коэффициенты отражения на входе встроенного коаксиального кабеля при
верхнем и нижнем по схеме положениях переключателя соответственно.
Все параметры полагаются постоянными, кроме параметров A, R и φR которые представляются полиномиальной или другой зависимостью от текущей частоты f или разности текущей и нижней частоты fH диапазона, в котором проводятся измерения:
|
|
(2) |
где с – скорость электромагнитной волны в вакууме;
остальные коэффициенты – параметры модели измерительного преобразователя.
При модуляции выражение для информационного сигнала второго детектора определяется разностью сигналов при разных положениях переключателя:
|
|
|
Коэффициенты
отражения
![]() и
и
![]() определяются следующими выражениями:
определяются следующими выражениями:
|
|
(3) |
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() –
S-параметры
кабельного разъема на выходе измерительного преобразователя;
–
S-параметры
кабельного разъема на выходе измерительного преобразователя;
Гx, ГIN – соответственно комплексные коэффициенты отражения тестируемой и встроенной нагрузок;
α, lcab, vф – соответственно коэффициент затухания, длина встроенного коаксиального кабеля и фазовая скорость распространения в нем электромагнитной волны.
Параметры кабельного разъема представляются следующими моделями:
|
|
(4) |
где X11, Y11, X22, Y22 – параметры, задающие начальные модуль и фазу;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() – параметры, учитывающие затухание сигнала в разъеме;
– параметры, учитывающие затухание сигнала в разъеме;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() – параметры, моделирующие эффективную длину разъема.
– параметры, моделирующие эффективную длину разъема.
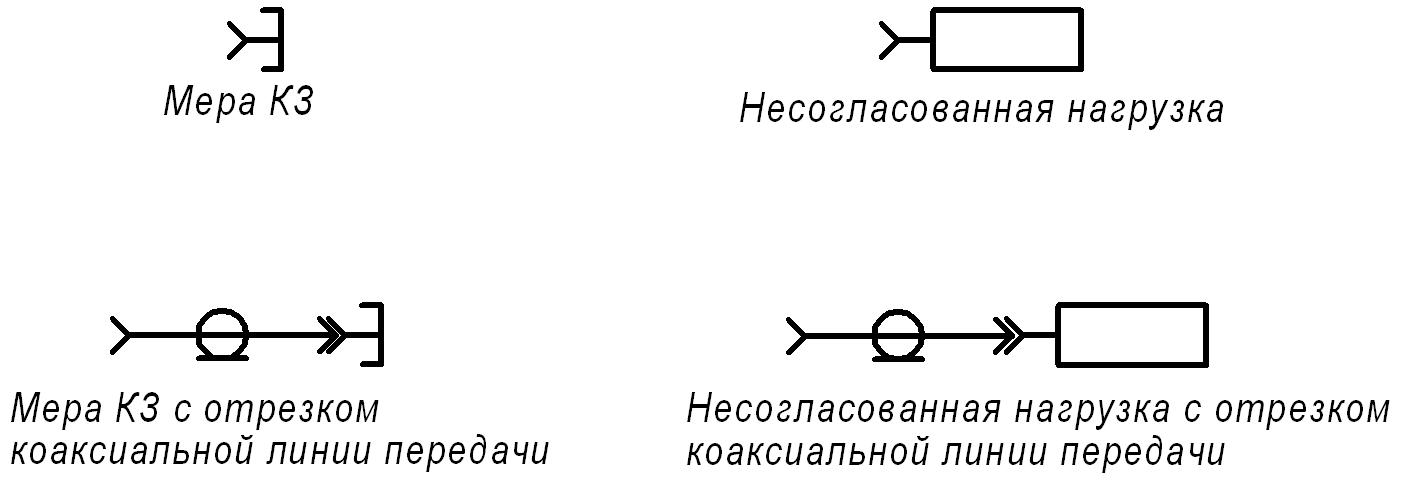
Для определения параметров модели измерительного преобразователя, входящих в выражения (1)–(4), выполняются 4 калибровочных измерения. Вместо тестируемой нагрузки поочередно подключаются известная мера короткого замыкания и неизвестная несогласованная нагрузка с модулем коэффициента отражения порядка 0,3 – непосредственно и через отрезок воздушной коаксиальной линии передачи известной длины (рис. 2).
Коэффициент отражения меры короткого замыкания описывается выражением:
|
|
(5) |
где lКЗ – известная длина меры.
|
Рисунок 2 – Виды используемых калибровочных мер
|
Математические модели коэффициентов отражения встроенной (ГIN), несогласованной калибровочной (ГНС) и тестируемой (Гx) нагрузок представляются моделями вида, аналогичного (5), с представлением модуля и аргумента либо частотно-независимыми, либо, например, полиномиальной зависимостью от частоты в пределах небольших частотных поддиапазонов (окон), на которые разделен анализируемый диапазон:
|
|
|
Параметры измерительного преобразователя при калибровочных измерениях определяются идентификацией в пространстве параметров измерительного преобразователя и неизвестной несогласованной калибровочной нагрузки. Аналогично определяются параметры тестируемой нагрузки при фиксированных на этапе калибровки параметрах измерительного преобразователя. Идентификация выполняется в частотных окнах [4] посредством минимизации целевых функции вида:
|
|
(6) |
где,
![]() и
и
![]() – измеренные информационные сигналы.
– измеренные информационные сигналы.
Для каждого из четырех
калибровочных измерений в выражение для
![]() в
(3) вместо Гx
подставляются соответственно ГIN,
ГНС,
и
в
(3) вместо Гx
подставляются соответственно ГIN,
ГНС,
и
![]() ,
,
![]() – при подключении короткозамкнутой и несогласованной нагрузок
через отрезок воздушной коаксиальной линии передачи (αcoax
и lcoax
– соответственно известные коэффициент затухания и физическая
длина отрезка).
– при подключении короткозамкнутой и несогласованной нагрузок
через отрезок воздушной коаксиальной линии передачи (αcoax
и lcoax
– соответственно известные коэффициент затухания и физическая
длина отрезка).
Калибровка и измерения проводятся во всех частотных окнах, на которые разделен анализируемый диапазон частот. Ширина частотных окон определяется адекватностью в его пределах моделей измерительного преобразователя и тестируемого резистивного компонента. Как правило, модель резистивного компонента предполагает медленную зависимость волновых параметров рассеяния от частоты, и ширина окон выбирается равной приблизительно 100 МГц. Для обеспечения корректной калибровки длина встроенного в измерительный преобразователь коаксиального кабеля должна обеспечивать не менее одного периода функций (3) в пределах частотного окна. Использование более сложных моделей измерительных преобразователей и испытуемых объектов для расширения частотных окон увеличивает количество искомых параметров и время выполнения математической обработки. Предварительные результаты математического моделирования, показали потенциально высокие точности измерительной системы при относительной её простоте.
- Литература:
- Кудрявцев А. М. Зондовые измерительные преобразователи для анализа элементов коаксиального тракта. / А. М. Кудрявцев, А. Б. Куликов, С. М. Никулин // Датчики и системы. – 2009, – № 8, С.33–36.
- Налькин М. Е. Анализ СВЧ цепей с амплитудным и гомодинным детектированием сигналов / М. Е. Налькин, С. М. Никулин, М. В. Пугин, В. П. Хилов // Датчики и системы. – 2003, – № 7, С.13–17.
- Кудрявцев А. М. Анализаторы цепей с зондовыми измерительными преобразователями. / А. М. Кудрявцев, А. Б. Куликов, С. М. Никулин // Измерительная техника. – 2009, – № 9, С.46–49.
- Кудрявцев А.М. Интеллектуальный анализ СВЧ цепей и антенн / А. М. Кудрявцев, С. М. Никулин. Учеб. пособие. Н. Новгород: НГТУ, 2005, 123 с.
Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы.