В данной статье рассмотрены контактные и бесконтактные методы измерения удельного сопротивления полупроводниковых материалов.
Ключевые слова: удельное сопротивление, контактный метод, бесконтактный метод, двухзондовый метод, однозондовый метод, четырехзондовый метод, метод Ван дер Пау.
При исследовании электрических свойств полупроводников и производстве полупроводниковых материалов, структур и приборов возникает необходимость измерения удельного электрического сопротивления полупроводниковых материалов. Измерение удельного сопротивления осуществляется не только для установления его значения, но также и для определения других важных параметров полупроводникового материала на основе теоретических расчетов или дополнительных экспериментальных данных. В идеальном случае измерение удельного сопротивления полупроводниковых материалов не должно приводить к разрушению образца и не должно требовать его специальной обработки.
Выделяют две группы методов измерения удельного сопротивления полупроводниковых материалов — контактные и бесконтактные. Многие методы основаны на измерении разницы потенциалов на некотором участке образца, через который пропускают электрический ток. При контактном методе происходит непосредственный контакт с полупроводниковым образцом, вследствие чего происходит разрушение образца. В связи с этим существует потребность в бесконтактных методах, в которых не требуется непосредственного контакта с образцом.
Для измерения удельного сопротивления образцов, имеющих правильную геометрическую форму и постоянное поперечное сечение, используют двухзондовый метод и однозондовый метод с дифференцированием сигнала. При использовании двухзондового метода на торцевых гранях образца, например в виде прямоугольной пластины, изготавливают омические контакты (К1 и К2). Через эти контакты вдоль образца пропускают электрический ток. На одной из поверхности образца вдоль линии тока устанавливаются два контакта в виде металлических иголок — зондов (З1 и З2), имеющих малую площадь соприкосновения и позволяющих изменить разность потенциалов. Между ними включен нулевой прибор Г и потенциометр П (рис.1.).
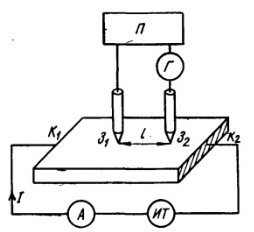
Рис. 1. Схема измерения удельного сопротивления двухзондовым методом
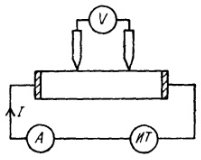
Рис. 2. Схема измерения с высокоомным вольтметром, включенным между зондами
Ток через образец подается от регулируемого источника (ИТ) постоянного тока, гарантирующего достаточную стабильность тока во времени. Сила тока измеряется миллиамперметром, а разность потенциалов — полуавтоматическим компенсирующим потенциометром или электронным цифровым вольтметром с высоким входным сопротивлением (рис. 2).
![]()
где ![]() — разность потенциалов между измерительным или потенциальными зондами, В;
— разность потенциалов между измерительным или потенциальными зондами, В; ![]() — сила тока, протекающего через образец, А;
— сила тока, протекающего через образец, А; ![]() — расстояние между зондами, см;
— расстояние между зондами, см; ![]() — площадь поперечного сечения,
— площадь поперечного сечения, ![]() ;
; ![]() — сопротивление участка образца между зондами;
— сопротивление участка образца между зондами; ![]() — удельное сопротивление,
— удельное сопротивление, ![]() .
.
Погрешность измерений напряжения и тока при использовании приборов с цифровой индикацией не превышает 0.1 %. Однако систематическая погрешность измерения между потенциальными зондами зависит от сопротивления контакта зонда с образцом, которое может в ![]() раз превышать сопротивление образца. Чтобы устранить влияние сопротивлений контактов на результат измерения, необходимо предельно уменьшить протекающий через них ток. Для этого используют вольтметры с высоким входным сопротивлением (
раз превышать сопротивление образца. Чтобы устранить влияние сопротивлений контактов на результат измерения, необходимо предельно уменьшить протекающий через них ток. Для этого используют вольтметры с высоким входным сопротивлением (![]() Ом и больше), причем сопротивление изоляции каждого из зондов относительно любого элемента измерительной установки должно быть больше этого значения.
Ом и больше), причем сопротивление изоляции каждого из зондов относительно любого элемента измерительной установки должно быть больше этого значения.
Отклонение реального контакта зонда от теоретической модели точечного потенциального контакта также вносит систематическую погрешность в результат измерения.
Модифицированным двухзондовым методом является однозондовый метод с дифференцированием сигнала (рис. 3).
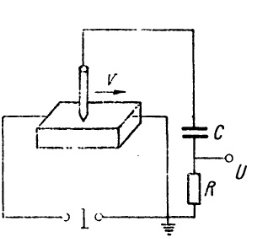
Рис. 3 Однозондовый метод с дифференцированием сигнала
В этом случае падение напряжения снимают между двумя зондами, один из которых неподвижен, а второй движется со скоростью ![]() . Сигнал поступает на дифференцирующую
. Сигнал поступает на дифференцирующую ![]() — цепочку. При этом удельное сопротивление может быть рассчитано по формуле:
— цепочку. При этом удельное сопротивление может быть рассчитано по формуле:
![]()
где ![]() — падение напряжение на сопротивлении
— падение напряжение на сопротивлении ![]() .
.
Таким образом, приведенная формула эквивалентна формуле для двухзондового метода с применением головки, в которой расстояние между зондами ![]() . Наиболее перспективен однозондовый метод при использовании движущегося зонда и введении в схему измерения дифференцирующего элемента. Разрешающая способность рассматриваемого метода однозначно определяется величиной эффективного межзондового расстояния
. Наиболее перспективен однозондовый метод при использовании движущегося зонда и введении в схему измерения дифференцирующего элемента. Разрешающая способность рассматриваемого метода однозначно определяется величиной эффективного межзондового расстояния ![]() . Поэтому при использовании однозондового метода для выявления микронеоднородностей необходимо выбирать оптимальные значение параметров
. Поэтому при использовании однозондового метода для выявления микронеоднородностей необходимо выбирать оптимальные значение параметров ![]() .
.
Особенностью однозондового, как и двухзондового, метода является возможность измерения некоторого среднего значения удельного сопротивления по всему сечению между точками, где расположены зонды, то есть с постоянным поперечным сечением.
Однако на производстве возникают задачи, которые нельзя выполнить рассмотренными методами. Примерами таких задач могут быть как измерение сопротивления материалов на различных участках полупроводникового слитка, не нарушая его целостности, так и определение удельного сопротивления материала в пластине неправильной геометрической формы. Такие задачи привели к созданию специальных методов определения удельного сопротивления без предъявления жестких требований к геометрии исследуемых образцов. Одним из таких методов является четырехзондовый метод.
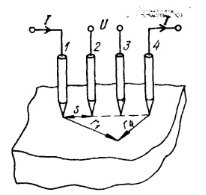
Рис. 4. Схема измерения удельного сопротивления четырехзондовым методом
Пусть на поверхности образца установлено четыре точечных зонда, как показано на рис. 4. Расстояние между соседними зондами ![]() , через два крайних зонда 1 и 4 проходит ток
, через два крайних зонда 1 и 4 проходит ток ![]() , который создает разность потенциалов
, который создает разность потенциалов ![]() между зондами 2 и 3. Разность потенциалов является функцией силы тока
между зондами 2 и 3. Разность потенциалов является функцией силы тока ![]() , удельного сопротивления
, удельного сопротивления ![]() , расстояния
, расстояния ![]() и геометрических размеров образцов.
и геометрических размеров образцов.
Разность потенциалов между зондами 2 и 3 находится по формуле:
![]()
Из выражения (3) находим удельное сопротивление ![]() Измерение разности потенциалов
Измерение разности потенциалов ![]() в четырехзондовом методе, производится, как и в двухзондовом методе. Влияние на результаты измерения неомических контактов потенциальных зондов 2 и 3 такое же.
в четырехзондовом методе, производится, как и в двухзондовом методе. Влияние на результаты измерения неомических контактов потенциальных зондов 2 и 3 такое же.
Четырехзондовый метод измерения широко используется в процессе производства полупроводниковых материалов и при создании полупроводниковых приборов. Выражения, связывающие ![]() и
и ![]() , получены для разных случаев. При расстоянии от зондов до поверхностей образца, значительно превышающих
, получены для разных случаев. При расстоянии от зондов до поверхностей образца, значительно превышающих ![]() , образец можно рассмотреть, как полупространство. И удельное сопротивление можно определить по выражению (3). Чем меньше
, образец можно рассмотреть, как полупространство. И удельное сопротивление можно определить по выражению (3). Чем меньше ![]() , тем для меньших образцов справедлива формула (3). На рис. 5 для двух значений
, тем для меньших образцов справедлива формула (3). На рис. 5 для двух значений ![]() показаны размеры образцов (в сантиметрах), при которых вычисление по формуле (3), не учитывающей их конечности, приводит к погрешности в 1 %.
показаны размеры образцов (в сантиметрах), при которых вычисление по формуле (3), не учитывающей их конечности, приводит к погрешности в 1 %.
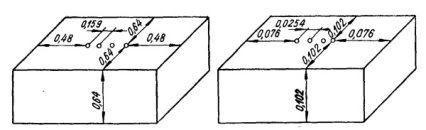
Рис. 5. Образцы разной геометрии
Двухкомбинационный четырех зондовый метод представляет собой разновидность четырехзондового метода при линейном расположении системы зондов, но в отличии от него измерение проводят дважды при различных комбинациях токовых и потенциальных зондов.
Благодаря высокой точности и упрощению процедуры измерения двухкомбинационный четырехзондовый метод используют для изучения распределения поверхности сопротивления ионно-легированных слоев по площади пластины. На основе данного метода созданы автоматизированные измерительные устройства с шаговым перемещением головки зонда по поверхности образца.
Ван дер Пау разработал модифицированный четырехзондовый метод, который применим для измерения удельного сопротивления плоских образцов (пластин) любой формы. При этом методе контакты располагаются по краям пластины (рис. 6). Пропуская ток ![]() через зонды 1 и 2, измеряют напряжение и вычисляют сопротивление между зондами 3 и 4:
через зонды 1 и 2, измеряют напряжение и вычисляют сопротивление между зондами 3 и 4: ![]() Затем, пропуская ток, через зонды 1 и 4, определяют сопротивление между зондами 2 и 3:
Затем, пропуская ток, через зонды 1 и 4, определяют сопротивление между зондами 2 и 3: ![]() .
.
Удельное сопротивление рассчитывают по формуле
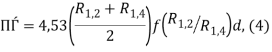
где ![]() — теоретически вычисленная корректирующая функция. Значение этой функции в зависимости от
— теоретически вычисленная корректирующая функция. Значение этой функции в зависимости от ![]() приведено на рис. 7.
приведено на рис. 7.
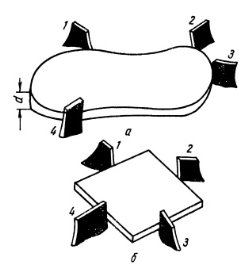
Рис. 6. Модифицированный четерехзондовый метод Ван дер Пау: а) измерение плоских пластин произвольной формы, б) расположение контактных зондов при разбраковке кристаллов
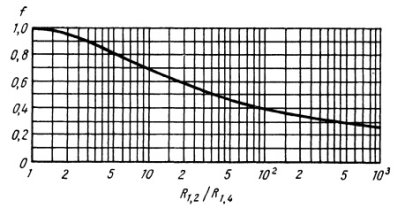
Рис. 7. Функция поправок ![]() в методе Ван дер Пау
в методе Ван дер Пау
Видно, что ![]() при
при ![]() . Как видно из соотношения (4), в расчетную формулу не входят расстояния между зондами. В формулах фигурируют величины, которые можно измерить с высокой точностью.
. Как видно из соотношения (4), в расчетную формулу не входят расстояния между зондами. В формулах фигурируют величины, которые можно измерить с высокой точностью.
Для пластин правильных геометрических размеров при ![]() удельное сопротивление можно определить с погрешностью менее 2 %.
удельное сопротивление можно определить с погрешностью менее 2 %.
Указанный метод можно применить для быстрой разбраковки пластин малого размера по удельному сопротивлению и концентрации (рис. 6).
В четырехзондовом методе и методе Ван дер Пау к токопроводящим контактам предъявляются те же требования, что и к двухзондовому методу: протекание через них тока не должно приводить к изменению концентрации носителей заряда в полупроводнике. Особенно это требование необходимо учитывать, если расстояние между зондами сравнимо с длиной диффузионного смещения носителей заряда или меньше его.
Рассмотренные выше методы приводят к разрушению образцов, поэтому рассмотрим бесконтактные методы, в которых не требуется непосредственный контакт с образцом. Общая идея бесконтактных методов определения удельного сопротивления состоит в следующем. В образце без использования контактов возбуждают ток, сила которого зависит от удельного сопротивления образца ![]() , которое определяют, измеряя какую-либо величину, функционально связанную с током. Для возбуждения тока образцы помещают в переменное магнитное, электрическое или, в общем случае, электромагнитное поле. О величине протекающего тока и удельном сопротивлении образца судят, измеряя силу взаимодействия тока с магнитным полем, либо измеряя величины, определяемые изменением энергии поля, в котором находится образец.
, которое определяют, измеряя какую-либо величину, функционально связанную с током. Для возбуждения тока образцы помещают в переменное магнитное, электрическое или, в общем случае, электромагнитное поле. О величине протекающего тока и удельном сопротивлении образца судят, измеряя силу взаимодействия тока с магнитным полем, либо измеряя величины, определяемые изменением энергии поля, в котором находится образец.
В качестве примера рассмотрим метод определения удельного сопротивления по силе взаимодействия, индуцируемого в образце, с магнитным полем. Пусть полупроводниковый образец в форме шрама помещен во вращающееся магнитное поле (рис. 8). Вектор индукции магнитного поля ![]() вращается в плоскости
вращается в плоскости ![]() с угловой частотой
с угловой частотой ![]() , а его абсолютная величина
, а его абсолютная величина ![]() остается неизменной. Поле индуцирует в образце ток. Взаимодействие этого поля с током приводит к возникновению момента сил
остается неизменной. Поле индуцирует в образце ток. Взаимодействие этого поля с током приводит к возникновению момента сил ![]() , который увлекает образец вслед за полем, то есть возникает ситуация, как в асинхронном двигателе. По величине момента сил можно определить удельное сопротивление образца.
, который увлекает образец вслед за полем, то есть возникает ситуация, как в асинхронном двигателе. По величине момента сил можно определить удельное сопротивление образца.
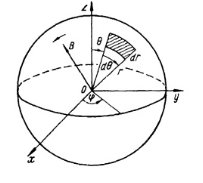
Рис. 8. Образец в форме шара во вращающемся магнитном поле
Для определения удельного сопротивления можно либо помещать образец во вращающееся магнитное поле, либо вращать образец в неизменном магнитном поле. В установке (рис. 9), использующей первую возможность, образец 1 подвешивается на тонкой упругой нити 2, к которой прикрепляется зеркальце 3, отражающей луч света 4. При включении магнитного поля образец, зеркальце и отражающий от него луч поворачивается. Угол поворота луча ![]() , где значение постоянной
, где значение постоянной ![]() определяется свойствами нитями, используя образец с известным удельным сопротивлением
определяется свойствами нитями, используя образец с известным удельным сопротивлением ![]() , для которого момент сил можно рассчитать по формуле:
, для которого момент сил можно рассчитать по формуле:
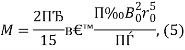
или
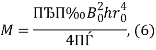
где в (5) ![]() — радиус образца; формула (6) используется для случая, когда образец имеет форму цилиндра с радиусом основания
— радиус образца; формула (6) используется для случая, когда образец имеет форму цилиндра с радиусом основания ![]() и высотой
и высотой ![]() . Измерив
. Измерив ![]() , определяют
, определяют ![]() , а затем вычисляют удельное сопротивление.
, а затем вычисляют удельное сопротивление.
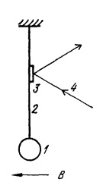
Рис. 9. К определению момента сил во вращающемся магнитном поле
Чем меньше удельное сопротивление, тем больше момент сил ![]() и проще проводить измерения. Метод ограничен со стороны больших
и проще проводить измерения. Метод ограничен со стороны больших ![]() . Изготовление образца в форме шара или цилиндра может вызвать затруднения. Такие методы наиболее эффективны при малых значениях удельного сопротивления образцов, когда действующие на них силы велики.
. Изготовление образца в форме шара или цилиндра может вызвать затруднения. Такие методы наиболее эффективны при малых значениях удельного сопротивления образцов, когда действующие на них силы велики.
Литература:
- Павлов, И. П. Методы измерения параметров полупроводниковых материалов: учеб. для вузов по спец. «Полупроводниковые и микроэлектронные приборы»./И. П. Павлов. — 2-е изд., перераб. и доп. — М.: Высш. шк., 1987. — 239 с., ил.
- Ковтонюк, Н.Ф, Измерение параметров полупроводниковых метериалов/Н. Ф. Ковтонюк, Ю. А. Концевой. — М.: Издательство «Металлургия», 1970. — 432с., ил.
- Воробьев, Ю. В. Методы исследования полупроводников/Ю. В. Воробьев, В.Н., Добровольский, В. И. Стриха. — Киев: Выща школа. Головное изд-во, 1988. — 232 с., ил.
- Батавин, В. В. Измерение параметров полупроводниковых материалов и структур/В. В. Батавин, Ю. А. Концевой, Ю. Ф. Федорович. — М.: Радио и связь, 1985. — 264 с., ил.

