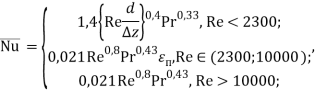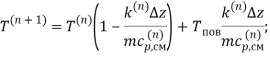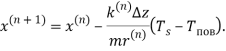Тепловой расчёт горизонтального трубопровода с учётом конденсации теплоносителя



Произведён расчёт системы отвода тепла в грунт для системы децентрализованной выработки тепловой и электрической энергии. При моделировании применялась гомогенная модель течения. Решена задача минимизации длины, потребной для охлаждения и конденсации теплоносителя, посредством определения оптимальных диаметральных размеров поперечного сечения трубопровода. Для оптимальных значений определено распределение массового паросодержания (степени сухости пара) по длине трубопровода.

Ключевые слова: децентрализованная выработка тепловой и электрической энергии, теплоотдача, тепловой расчёт, конденсация, гомогенная модель течения.

Введение

Централизованное тепло- и энергообеспечение на данный момент является наиболее распространённым в Российской Федерации, однако оно имеет ряд существенных недостатков: большая длина линий передач и магистралей создаёт большие потери в окружающую среду; необходимость трансформации энергии; возможность крупной аварии, что может привести к обесточиванию большого числа потребителей. В этой связи, актуальность приобретает идея децентрализации — генерации тепловой и электрической энергии независимо от централизованных источников в непосредственной близости к местам её потребления. Децентрализованная выработка позволяет обеспечить теплом и электричеством широкий круг потребителей вне зависимости от их географического положения при более низкой стоимости. Более того, децентрализация позволяет обеспечить резервное снабжение энергией объектов социальной инфраструктуры (больницы, школы, детские сады и т. п.).

В работе [1] была предложена схема децентрализованной выработки энергии с применением органического цикла Ренкина. Рабочее тело (РТ), нагреваясь и превращаясь в пар в котле, попадает в турбину и совершает полезную работу. Затем оно попадает в конденсатор, конденсируется и с помощью насоса подается обратно в котёл. Турбина вращает электрогенератор за счет чего и вырабатывается электроэнергия. В данной статье рассматривается один из вариантов отвода тепла РТ к холодному источнику — окружающей среде — при помощи горизонтального трубопровода круглого сечения — конденсатора. В статье описан инженерный термодинамический расчёт данного конденсатора, оптимизация его поперечных геометрических размеров, при которых его длина минимальна.

Расчётная модель конденсатора (рис. 1) представляет собой горизонтально расположенную трубу, помещенную в грунт на глубину , с наружным диаметром и толщиной . Материал конструкции — нержавеющая сталь 08Х17Т, с постоянной теплопроводностью [2].

Расчётная модель окружена грунтом с постоянной теплопроводностью

, что соответствует глине средней влажности [3].

Температура поверхности грунта принята постоянной , что соответствует среднегодовой температуре поверхности грунта в г. Уфа [4], температура на входе в трубопровод принята , расход [5].

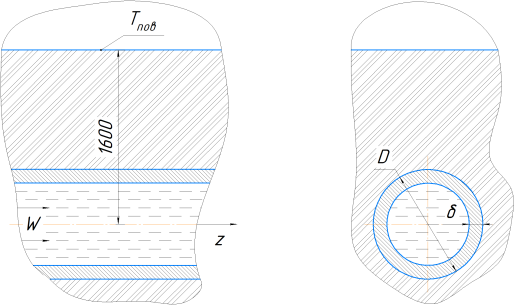
Рис. 1. Расчетная область

В качестве рабочего тела принят толуол, зависимости теплофизических свойств (ТФС) (плотность, коэффициент теплопроводности, коэффициент динамической вязкости, удельная изобарная теплоемкость, теплота парообразования) жидкой и парообразной фаз которого определены посредством аппроксимации данных из программы REFPROP [6] и источников [7, 8].

С целью упрощения моделирования в данном исследовании принят ряд допущений. Применяемые аппроксимирующие зависимости характеризуют изменение ТФС только от температуры, так как влияние давления имеет более низкий порядок. Также пренебрегаем потерями напора из-за трения. Моделируется изменение параметров РТ только вдоль оси трубопровода . Влияние сил гравитации также не учитывается. Вследствие малости, составляющая кинетической энергии потока в уравнении энергии не учитывается.

Расчёт проводится в 2 этапа.

Этап 1: расчёт охлаждения перегретого пара, поступающего из турбины, до расчётного сечения, где температура пара достигает точки насыщения

, конденсации перегретого пара ещё не наблюдается, так как, предполагается, что температура стенки выше температуры насыщения.

Этап 2: расчёт течения парожидкостной смеси с конденсацией пара.

Во втором этапе исследование двухфазного течения проводится при помощи гомогенной модели, которая рассматривает РТ как «псевдожидкость» с изменяющимися свойствами за счёт роста массовой доли жидкости в ней. Вдобавок, не рассматривается поверхность раздела фаз. Допускается, что фазы движутся с одинаковыми скоростями. ТФС пара и жидкости берутся в точке насыщения, затем усредняются по массовому паросодержанию [9]:

((1)

где 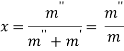— массовое паросодержание (показывает массовую долю пара в двухфазном потоке, степень сухости); , — массовые расходы, , , — коэффициенты теплопроводности, , , — коэффициенты динамической вязкости, , , — удельные изобарные теплоемкости, , , — плотности жидкой (), парообразной () фаз и их смеси (.

Таким образом, благодаря данным допущениям, описание изменения паросодержания по длине трубы возможно уравнениями гидрогазодинамики однофазной среды.

Описание методики расчёта

Из уравнения теплового баланса с учётом закона Ньютона-Рихмана получим изменение энтальпии потока вдоль оси трубы за счёт теплоотвода:

((2)

где — линейный суммарный коэффициент теплоотдачи.

В формуле (2) в зависимости от этапа расчёта, за определяющую принимается либо теплоемкость пара, либо теплоемкость смеси, рассчитываемая по формуле из (1). Знак минус говорит отводе энергии от теплоносителя.

В отсутствие скачкообразных градиентов давления, изменение массового паросодержания на втором этапе расчёта зависит только от изменения энтальпии:

((3)

где — удельная теплота парообразования.

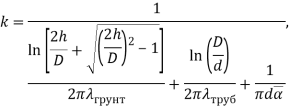
Из условия того, что при установившемся режиме тепловой поток постоянен, была определена формула для суммарного линейного коэффициента теплоотдачи через цилиндрическую стенку и полубесконечный массив (грунт) [9]:

((4)

где — средний на выбранном дискретном малом участке коэффициент теплоотдачи от потока пара или смеси, — внутренний диаметр трубы.

Средний коэффициент теплоотдачи от потока пара или смеси определяется в зависимости от числа Нуссельта:

((5)

где — среднее на участке длины трубопровода число Нуссельта. В качестве определяющего принимается либо коэффициент теплопроводности пара, либо коэффициент теплопроводности смеси (см. формулу (1)) в зависимости от этапа расчёта.

В свою очередь, число Нуссельта потока зависит от режима течения [10]:

((6)

где — число Рейнольдса, (определяющие ТФС принимаются в зависимости от этапа расчёта), — поправка на переходный режим, зависящая от числа Рейнольдса [11].

Уравнения (1)–(6) с граничными условиями образуют замкнутую систему уравнений для теплового расчёта трубопровода с учетом конденсации теплоносителя.

Решение задачи произведено посредством явной разностной схемой. Аппроксимация уравнений (2) и (3) конечными разностями даёт:

	((7)
	((8)

Решение (7) устойчиво при условии: 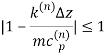( — номер расчётного сечения) [12]. Данный критерий использован для определения шага по координате . Решение (8) устойчиво при любом шаге, однако для гладкости решения шаги примем одинаковыми.

На первом этапе расчёт завершается при достижении , на втором — при .

Потребная длина трубопровода при данных диаметральных размерах определяется как произведение количества расчётных сечений и длины шага.

Анализ полученных результатов

На рис. 2 приведены результаты расчёта суммарных длин трубопровода в зависимости от наружного диаметра и толщины стенки трубопровода. Построение зависимостей произведено с помощи итерационного расчёта. Толщина варьировалась в пределах , а наружный диаметр — .

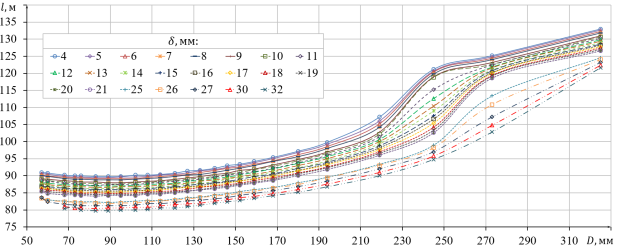
Рис. 2. Зависимость суммарных длин трубопровода от наружного диаметра и толщины

Из анализа графиков следует, что минимальные значения наблюдаются при и . В свою очередь, конкретное оптимальное значение достигается при и .

Стоит отметить, что оптимумы лежат в областях с такими значениями и , при которых наблюдается одновременно и достаточно большое число Рейнольдса на большей части трубопровода, и низкая сумма термических сопротивлений стенки трубы и грунта. Так, с увеличением толщины трубы на при фиксированном диаметре её потребная суммарная длина уменьшается на , а с увеличением наружного диаметра на при фиксированной толщине длина уменьшается на (до оптимального ), затем увеличивается на . Согласно полученным зависимостям (рис. 2), в области значений до перегиба графиков () количество расчётных сечений со сверхкритическими имеет превалирующее значение (турбулентный режим наблюдается, в среднем, на участка конденсации ). В области перегибов графиков, где графики начинают стремительный рост с увеличением , и после неё наблюдается увеличение количества сечений с переходными и докритическими , что несомненно ведет к снижению теплосъема с РТ и увеличению необходимой длины .

На рис. 3 представлено распределение массового паросодержания по длине трубы при и (оптимальные значения). Очевидно, что функция близка к линейной, так как суммарный линейный коэффициент теплоотдачи при конденсации варьируется в пределах , а другие параметры, входящие в зависимость (3), берутся в точке насыщения или постоянны.

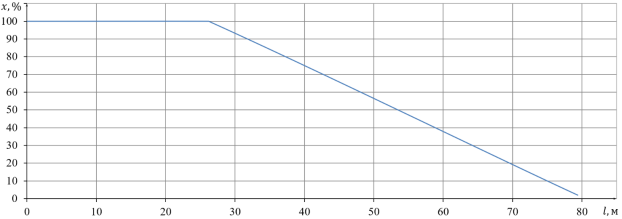
Рис. 3. Изменение степени сухости пара для оптимальной длины конденсатора

Выводы

В ходе данного исследования рассмотрен один из вариантов отдачи тепла РТ холодному источнику (грунту) в горизонтальном трубопроводе системы децентрализованной выработки тепловой и электрической энергии. Проведено моделирование охлаждения и конденсации теплоносителя при помощи гомогенной модели течения. С целью оптимизации потребной длины трубы, моделирование произведено при различных поперечных геометрических размерах трубопровода. По результатам итерационного расчёта установлен характер зависимости длины от наружного диаметра и толщины . Определено, что длина, требуемая для охлаждения и конденсации пара, достигает минимума () при и . На этапе конденсации зависимость изменения массового паросодержания близка к линейной.

Для упрощения расчёта в данном исследовании принято предположение об однородности потока РТ, как в динамическом, так и в тепловом отношении. Это позволило заметно упростить расчёт. Однако, в силу своих особенностей, гомогенная модель даёт сравнительно приближённое представление о поведении потока конденсирующегося пара, что в итоге, может привести к завышению необходимой для конденсации РТ длины трубопровода.

Литература:

1. Кишалов, А. Е., Зародов, Е. А. Термодинамический расчёт органического цикла Ренкина для энергоустановок малой мощности с использованием биотоплива // Молодежный Вестник УГАТУ — 2017 — № 2(17) — С. 183–188.
2. Характеристика материала 08Х17Т // Марочник стали и сплавов [Электронный ресурс] URL: http://www.splav-kharkov.com/mat_start.php?name_id=319 (дата обращения: 01.10.2018)
3. Thermalinfo.ru // Теплопроводность горных пород и минералов, их плотность и теплоемкость [Электронный ресурс]. — URL: http://thermalinfo.ru/svojstva-materialov/mineraly/teploprovodnost-gornyh-porod-i-mineralov-ih-plotnost-i-teploemkost (дата обращения: 01.10.2018)
4. Волков, М. М. Справочник работника газовой промышленности [Текст] / М. М. Волков, А. Л. Михеев, Конев К. А. — 2-е изд., перераб. и доп. — М.: Недра, 1989. — 286 с.
5. Кишалов, А. Е., Зародов, Е. А. Способ конденсации рабочего тела в ОЦР за счёт температуры грунта // Мавлютовские чтения: Материалы XI Всероссийской молодежной научной конференции: в 7 т. / Том 1 / Уфимск. гос. авиац. техн. ун-т. — Уфа: РИК УГАТУ, 2017. — С. 371–375.
6. NIST REFPROP [Электронный ресурс]. — URL: https://www.nist.gov/srd/refprop (дата обращения: 01.10.2018).
7. Варгафтик, Н. Б. Справочник по теплофизическим свойствам газов и жидкостей [Текст] / Н. Б. Варгафтик. — М.: Государственное издательство физико-математической литературы, 1963. — 708 с.
8. Варгафтик, Н. Б. Справочник по теплопроводности жидкостей и газов [Текст] / Н. Б. Варгафтик и др. — М: Энергоатомиздат, 1990. — 352 с.
9. Уоллис, Г. Одномерные двухфазные течения [Текст] / Г. Уоллис. — М.: Мир,
10. 1972. — 440 с.
11. Кутателадзе, С. С. Основы теории теплообмена [Текст] / C. C. Кутателадзе — Изд. 5-е перераб. и доп. — М. Атомиздат, 1979. — 416 с.
12. Лашутина, Н. Г. Техническая термодинамика с основами теплопередачи и гидравлики [Текст]: учебное пособие / Н. Г. Лашутина, О. В. Макашова, Р. М. Медведев. — Л.: Машиностроение, 1988. — 336 с.
13. Бахвалов, Н. С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения) [Текст] / Н. С. Бахвалов. — М.: Главная редакция физико-математической литературы изд-ва «Наука», 1975. — 631 с.