Исследование процессов обработки и преобразования параметров тестовых заданий в интеллектуальной обучающей системе
Авторы: Прошкина Елена Николаевна, Балашова Ирина Юрьевна
Рубрика: 1. Информатика и кибернетика
Опубликовано в
VI международная научная конференция «Современные тенденции технических наук» (Казань, май 2018)
Дата публикации: 18.03.2018
Статья просмотрена: 66 раз
Библиографическое описание:
Прошкина, Е. Н. Исследование процессов обработки и преобразования параметров тестовых заданий в интеллектуальной обучающей системе / Е. Н. Прошкина, И. Ю. Балашова. — Текст : непосредственный // Современные тенденции технических наук : материалы VI Междунар. науч. конф. (г. Казань, май 2018 г.). — Казань : Молодой ученый, 2018. — С. 13-16. — URL: https://moluch.ru/conf/tech/archive/300/13986/ (дата обращения: 23.04.2024).
В статье рассматриваются вопросы калибровки банка тестовых заданий в интеллектуальной обучающей системе. Выделяются уровни сложности заданий, что позволяет наложить на них дополнительные ограничения, и приводится диапазон сложности заданий для каждого уровня.
Ключевые слова: подготовленность испытуемого, трудность задания, логит, уровень сложности, однопараметрическая модель Раша.
В настоящее время в результате высокой востребованности образовательной услуги возникает необходимость произвести преобразование системы образования с использованием современных информационных технологий. Особое внимание уделяется созданию и сопровождению интеллектуальных обучающих систем открытого и дистанционного обучения, развитию новых объектных технологий, созданию баз учебных материалов, наряду с развитием традиционных технологий.
Интеллектуальная обучающая система (ИОС) — это автоматизированная обучающая система, имеющая интеллектуальный интерфейс, позволяющая в процессе обучения вести диалог, отвечать на вопросы и выполнять задания на естественном языке. Целью ИОС, помимо предоставления информации, является диагностика знаний обучающегося и предоставление возможности исправления им ошибок.
С начала XXI в. в образовании появилось новое направление оценки знаний обучающихся — компьютерное тестирование. Тестирование является одним из основных этапов промежуточной и итоговой аттестации в образовательных учреждениях [1]. Основным критерием подготовленности испытуемых при обычном тестировании является набранный балл обучающихся — первичный балл. Однако первичный балл является всего лишь сравнительной оценкой. Он существенно зависит от случайного выбора тестовых заданий и при другом тестировании может оказаться иным [2]. При этом необходимо понимать, что уровень подготовки является латентным (скрытым) параметром и непосредственному измерению не поддается — он может быть только оценен на этапе проверки знаний с определенной вероятностью.
Для объективной оценки подготовленности испытуемых использование модели тестирования с привлечением только классической теории тестов является недостаточной, так как уровень приобретенных знаний и уровень сложности тестовых заданий имеют разную метрику [3].
В основе современной теории тестов лежит Item Response Theory (IRT). IRT предназначена для выполнения оценки латентных параметров испытуемых и заданий тестов на основе математико-статистических моделей измерения. IRT является частью более общей теории латентно-структурного анализа (LSA). Данная теория намного эффективнее традиционной теории тестов, поскольку позволяет получать более высокие величины таких параметров, как точность, уровень измерений и качество тестов [4]. Основным предположением IRT является наличие взаимосвязи между наблюдаемыми результатами учебных достижений, латентными свойствами самих тестируемых (подготовленность по предмету на момент тестирования) и характеристиками используемых тестовых заданий (уровнями трудности).
Будем использовать в качестве математической модели однопараметрическую модель Раша. В рамках этой модели задания характеризуются только одним параметром — трудностью. Вероятность правильного ответа на задание трудностью ![]() для испытуемого с уровнем подготовленности
для испытуемого с уровнем подготовленности ![]() выражается зависимостью:
выражается зависимостью:
![]() ,
,
где
При практическом применении теории IRT высчитывают начальные оценки параметра подготовленности испытуемых и параметра трудности тестовых заданий. Начальные оценки параметра подготовки учащихся в логитах находят по формуле:
![]() ,
,
где ![]() — уровень подготовленности i-го ученика,
— уровень подготовленности i-го ученика, ![]() и
и ![]() — доли правильных и неправильных ответов соответственно, подсчитанные по матрице наблюдаемых результатов выполнения теста. Начальные оценки параметра трудности заданий
— доли правильных и неправильных ответов соответственно, подсчитанные по матрице наблюдаемых результатов выполнения теста. Начальные оценки параметра трудности заданий ![]() получают по формуле:
получают по формуле:
![]() ,
,
где ![]() — уровень трудности j-го задания,
— уровень трудности j-го задания, ![]() и
и ![]() — доли правильных и неправильных ответов соответственно на j-е задание, подсчитанные по матрице наблюдаемых результатов выполнения теста.
— доли правильных и неправильных ответов соответственно на j-е задание, подсчитанные по матрице наблюдаемых результатов выполнения теста.
Указанные параметры, уровень подготовленности и значение трудности задания, представляют наибольший интерес при создании нашей интеллектуальной обучающей системы.
Для создания адаптивного теста необходимо иметь хороший банк тестовых заданий с известными уровнями трудности (калиброванных заданий). Базу тестовых заданий предварительно будем разделять на различные уровни сложности: легкий (первый уровень сложности), средний (второй уровень), высокий (третий уровень). Будем считать, что уровень сложности указывается экспертом на этапе регистрации тестового задания.
Введем следующие правила:
– логика «И» — это правило, по которому начисляется максимальное количество баллов при условии, что выбраны все правильные варианты ответа и не выбраны неправильные;
– логика «ИЛИ» — правило, по которому начисляются баллы ответа при условии, что выбран хотя бы один правильный ответ и отнимаются баллы ответа, если выбран неправильный.
Дополнительно введем ограничения:
– для первого уровня сложности допускаются только задания с однозначным выбором ответов;
– для второго уровня сложности допускаются задания с множественным выбором с добавкой веса по логике «ИЛИ», вопросы с множественным выбором по логике «И» и вопросы с однозначным ответом;
– для третьего уровня сложности допускаются задания любого типа.
При оценке ответов первого уровня сложности будем считать, что за правильное решение начисляется 1 балл, за неправильное — 0 баллов.
При оценке ответов второго уровня сложности будем считать, что за правильное решение заданий с однозначным выбором ответов начисляется 2 балла, за неправильное — 0 баллов. За решение заданий с выбором ответом будем исходить из следующего принципа: за правильное решение — 2 балла, за решение, в котором правильно более 50 % вариантов — 1 балл, иначе 0 баллов:
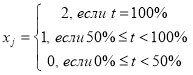 ,
,
где ![]() — это балл за решение задания,
— это балл за решение задания, ![]() – количество правильно выбранных ответов в задании.
– количество правильно выбранных ответов в задании.
При оценке ответов третьего уровня сложности будем считать, что за правильное решение заданий с однозначным выбором ответов начисляется 4 балла, за неправильное — 0 баллов. За решение заданий с выбором ответом будем исходить из следующего принципа: за правильное решение — 4 балла; за решение, в котором правильно более 75 % вариантов — 3 балла; за решение, в котором правильно более 50 % вариантов, но менее 75 % — 2 балла; за решение, в котором правильно более 25 % вариантов, но менее 50 % — 1 балл, иначе 0 баллов:
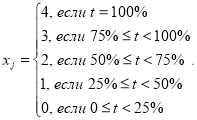
Ранее было определено, что порядок сложности задания задается на этапе регистрации задания в банке заданий. При этом необходимо учитывать, что в результате выполнении калибровки может оказаться, что задание не соответствует изначально указанному уровню сложности. Поэтому процесс калибровки базы заданий будем выполнять по следующему алгоритму.
Степень сложности задания
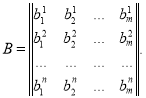
Номера столбцов матрицы B соответствуют номерам предложенных при тестировании заданий, номера строк соответствуют номерам испытуемых групп.
Дополнительно введем обозначение ![]() — процент испытуемых, правильно решивших j-ое задание. Определим для каждого типа задания процент испытуемых, справившихся с заданием и уровень сложности заданий согласно вышеприведенным формулам. Результаты представим в виде таблицы (табл. 1).
— процент испытуемых, правильно решивших j-ое задание. Определим для каждого типа задания процент испытуемых, справившихся с заданием и уровень сложности заданий согласно вышеприведенным формулам. Результаты представим в виде таблицы (табл. 1).
Таблица 1
Параметры калибровки заданий
|
Уровень сложности |
Первый уровень |
Второй уровень |
Третий уровень |
||||
|
Тип заданий |
однозначный |
однозначный |
ИЛИ |
И |
однозначный |
ИЛИ |
И |
|
% решений |
[75;100] |
[50;90] |
[40;90] |
[40;80] |
[10;50] |
[0;40] |
|
|
Степень сложности |
[- |
[-2,197; 0] |
[-2,197; 0,405] |
[-1,386; 0,405] |
[0; 2,197] |
[0,405; + |
|
Составленная таблица позволяет соотносить между собой результаты по различным тестам.
Таким образом, деление банка тестовых заданий по уровням сложности с применением калибровки внутри каждого уровня позволит более эффективно организовать банк тестовых заданий, так как деление на группы сложности позволяет наложить дополнительные ограничения на задания и установить диапазон допустимой сложности заданий.
Литература:
- Алещанова И. В., Фролова Н. А. Тестирование как средство повышения качества контроля и оценки эффективности учебного процесса в вузе // Современные проблемы науки и образования.–2007.–№ 6.–С.13–14.
- Аванесов В. С. Композиция тестовых заданий — М.: Центр тестирования, 2002. — 237 с.
- Челышкова М. Б. Теория и практика конструирования педагогических тестов — М.: Логос, 2002. — 432 с.
- Майоров А. Н. Теория и практика создания тестов для системы образования — М.: «Интеллект-центр», 2001. — 296 с.
Ключевые слова
подготовленность испытуемого, трудность задания, логит, уровень сложности, однопараметрическая модель РашаПохожие статьи
Подходы к определению уровня сложности тестовых заданий
Таким образом, система заданий третьего уровня сложности должны носить элементы творчества.
задание, ответ, тестовое задание, THEN, закрытая форма, установление соответствия, правильный ответ, Кыргызская литература, множественный выбор, тестовая...
Разработка web-ориентированной экспертной системы оценки...
Для программной реализации web-ориентированной экспертной системы оценки качества педагогических тестов выбрана однопараметрическая модель Г. Раша, так как данная модель не требует
- получать уровни подготовленности обучаемых и уровни сложности заданий
Интеллектуальные системы поддержки принятия решений
Однако необходимость учета при принятии управленческих решений большого количества экономических, политических, социальных, правовых факторов существенно усложняет процесс выбора правильного варианта решения. Как правило, это связано со сложностями...
Разновидности заданий в тестовой форме | Статья в сборнике...
Задание с множественным выбором (с выбором несколько правильных ответов). Под тестовым заданием с выбором нескольких правильных ответов понимают тестовое задание закрытой формы в котором допускается выбор нескольких правильных ответов из числа...
Использование тестового контроля на примере системы Moodle...
Это и выбор типа лекционного материала, и выбор уровня сложности практических занятий.
Множественный выбор — позволяет выбрать один или несколько ответов из заданного списка. Причем при создании вопроса с одним правильным ответом система...
Разноуровневые задания как средство оценивания в процессе...
Задания традиционно делятся по уровню сложности на репродуктивные, реконструктивные и творческие.
Здесь можно использовать следующие задания: Отметьте/выберите правильный вариант ответа.
Проблемы внедрения системы тестирования в современной школе
Опыт внедрения приведенных выше нововведений на уровне ЕНТ показал неоднозначные, а иногда и просто поразительные результаты.
– Закрытые тестовые задания — относятся к заданиям, на которые даются готовые ответы на выбор, из них один правильный...
Методика объективной оценки деятельности студента педвуза
Сравнение ответа студентов с эталоном по числу правильно выполненных студентами операций (а) теста дает возможность
Задачи третьего уровня: для решения требуется исследовательский подход при построении педагогической модели ситуации, изучении нового...
Похожие статьи
Подходы к определению уровня сложности тестовых заданий
Таким образом, система заданий третьего уровня сложности должны носить элементы творчества.
задание, ответ, тестовое задание, THEN, закрытая форма, установление соответствия, правильный ответ, Кыргызская литература, множественный выбор, тестовая...
Разработка web-ориентированной экспертной системы оценки...
Для программной реализации web-ориентированной экспертной системы оценки качества педагогических тестов выбрана однопараметрическая модель Г. Раша, так как данная модель не требует
- получать уровни подготовленности обучаемых и уровни сложности заданий
Интеллектуальные системы поддержки принятия решений
Однако необходимость учета при принятии управленческих решений большого количества экономических, политических, социальных, правовых факторов существенно усложняет процесс выбора правильного варианта решения. Как правило, это связано со сложностями...
Разновидности заданий в тестовой форме | Статья в сборнике...
Задание с множественным выбором (с выбором несколько правильных ответов). Под тестовым заданием с выбором нескольких правильных ответов понимают тестовое задание закрытой формы в котором допускается выбор нескольких правильных ответов из числа...
Использование тестового контроля на примере системы Moodle...
Это и выбор типа лекционного материала, и выбор уровня сложности практических занятий.
Множественный выбор — позволяет выбрать один или несколько ответов из заданного списка. Причем при создании вопроса с одним правильным ответом система...
Разноуровневые задания как средство оценивания в процессе...
Задания традиционно делятся по уровню сложности на репродуктивные, реконструктивные и творческие.
Здесь можно использовать следующие задания: Отметьте/выберите правильный вариант ответа.
Проблемы внедрения системы тестирования в современной школе
Опыт внедрения приведенных выше нововведений на уровне ЕНТ показал неоднозначные, а иногда и просто поразительные результаты.
– Закрытые тестовые задания — относятся к заданиям, на которые даются готовые ответы на выбор, из них один правильный...
Методика объективной оценки деятельности студента педвуза
Сравнение ответа студентов с эталоном по числу правильно выполненных студентами операций (а) теста дает возможность
Задачи третьего уровня: для решения требуется исследовательский подход при построении педагогической модели ситуации, изучении нового...











