Разработка КИХ-фильтра с использованием распределенной арифметической архитектуры



Введение

Сигнал — это функция независимой переменной, которая содержит информацию. Среди методов обработки сигналов существуют аналоговая обработка сигналов и цифровая обработка сигналов. В обработке аналоговых сигналов присутствуют как входные, так и выходные непрерывные сигналы, а в обработке цифровых сигналов вход и выход представляют собой дискретные сигналы. Так как цифровые приборы в наше время очень широко распространены, то обработка цифровых сигналов очень востребована. Обрабатывая сигнал нам нужно удалить шум от информации и фильтр как раз помогает с этой задачей. Он представляет из себя частотно-избирательную сеть, которая модифицирует входной сигнал для облегчения дальнейшей обработки этого сигнала. В цепи обработки сигналов фильтр — это устройство или алгоритм, который удаляет части сигнала. Он выбирает, подавлять или модифицировать определенные частотные составляющие сигнала, либо для уменьшения шума, либо для формирования спектра.

Существуют два типа фильтров: аналоговые фильтры и цифровые. Аналоговый фильтр работает с напряжением, тогда как цифровой фильтр работает с дискретными сигналами. У цифровых фильтров лучшее соотношение сигнал/шум, лучшая воспроизводимость, и они выполняют бесшумные математические операции. Среди цифровых фильтров есть два наиболее распространенных, это фильтр с конечной импульсной характеристикой (КИХ) и фильтр с бесконечной импульсной характеристикой (БИХ). КИХ фильтр по своей природе является нерекурсивным а БИХ рекурсивным. КИХ-фильтр — это фильтр, импульсная характеристика которого или ответ на любой вход с конечной длиной, имеет конечную длительность, так как он оканчивается на ноль за конечное время. Фильтры БИХ имеют внутреннюю обратную связь и могут продолжать отвечать в течение неопределенного срока. КИХ-фильтр может использоваться для реализации практически любого вида частотной характеристики в цифровом виде и реализуется с помощью умножителей, сумматоров и элементов задержки.

Как уже было ранее сказано, цифровая обработка сигналов имеет широкий спектр применений. Она широко используются в обработке мультимедийных аудиосигналов, из которых удаляется шум. В цифровой обработке сигналов цифровые фильтры являются важными элементами. Проектирование цифрового фильтра — это процесс вычисления соответствующих коэффициентов фильтра и порядка цифрового фильтра. Из-за его стабильности предпочтительно использовать КИХ-фильтры. Основное представление КИХ-фильтра дается формулой (1).

(1)

где y(n) — выходной отклик, x(n) — входной сигнал и представляет коэффициенты фильтра для КИХ-фильтра порядка M. Прямая реализация такого КИХ-фильтра показана на рис. 1.

В представлении прямой формы КИХ-фильтр может быть реализован с использованием сумматоров, умножителей и элементов задержки. Но умножители ограничивают скорость работы всей схемы. Для решения данной проблемы, мы можем заменить множители на сдвиговые регистры с сумматорами, что в сумме из себя представляют ускоренный умножитель, в котором набор констант (здесь h₀, h₁,...) умножается на переменную x(n). Но недостаток в такой замене заключается в том, что увеличение сложности схемы и производительности трудно предсказать. Таким образом, мы переходим к другой архитектуре, называемой распределенной арифметикой, которая представляет собой архитектуру с меньшим множителем. Распределенная арифметика использует таблицы поиска, элементы задержки и накопители. Таким образом, он увеличивает скорость процесса фильтрации и потребляет меньше площади и, следовательно, экономит ресурсы.

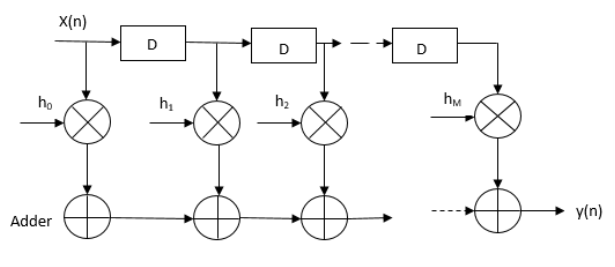
Рис. 1. Прямое представление КИХ-фильтра порядка M

Планируемая работа

Для того чтобы сделать расчеты умножения с накоплением более эффективными будем использовать распределенную арифметику. Данный метод носит последовательный характер. Распределенная арифметика подходит тогда, когда количество элементов в векторе почти такое же, как размер слова. В распределенной арифметике, просмотр ROM может заменить явный процесс умножения. Таким образом, мы можем эффективно внедрить КИХ-фильтр в ПЛИС. На рис.2 показана базовая блок-схема структуры фильтра КИХ с использованием распределенной арифметики.

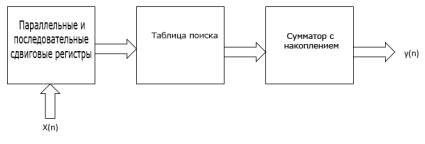
Рис. 2. Базовая блок-схема структуры фильтра КИХ с использованием РА

Он включает в себя три блока — параллельные и последовательные регистры сдвига, таблицу поиска и сумматоры с накопителем. Здесь x(n) — входной сигнал, а y(n) — выходной сигнал. Выходной отклик линейного, не зависящего от времени фильтра в любое дискретное время определяется формулой (2)

(2)

Пусть X_k будет N — размерное число представленное в дополнительном коде. Его вид будет таким {b_k0, b_k1, b_k2,......, bk_(N-1)} где b_k0 это бит который определяет знак числа (если он равен 1 то число отрицательное, если 0 то положительное). Таким образом X_k можно выразить в виде формулы 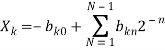(3)

(3)

Подставив 3-ю формулу во 2-ю и решив ее, мы получим формулу 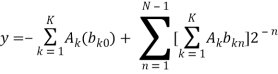(4)

(4)

В таблице № 1 показано, как простая таблица поиска для распределенной арифметики использует 3 коэффициента A₀, A₁, A₂. Соответствующее значение выбирается на основе выходных значений сдвигового регистра.

Результаты

В итоге с помощью Xilinx ISE 14.7 был разработан КИХ-фильтр с использованием распределенной арифметики. Программирование выполнялось для ПЛИС Spartan 3E-1200 на языке VHDL. Результаты выходного сигнала показаны на рисунке 3.

Таблица 1

Таблица поиска для трех коэффициентов

b2b1b0	Значение
000	0
001	A0
010	A1
011	A1 + A0
100	A2
101	A2 + A0
110	A2 + A1
111	A2 + A1+ A0

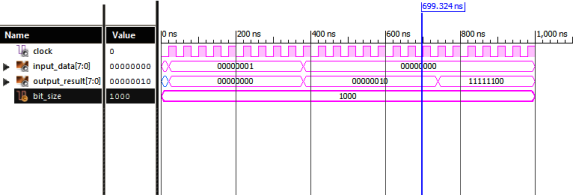
Рис. 3. Выходная характеристика КИХ-фильтра с использованием распределенной арифметики

Рис. 4. Обозначение КИХ-фильтра с использованием распределенной арифметики.

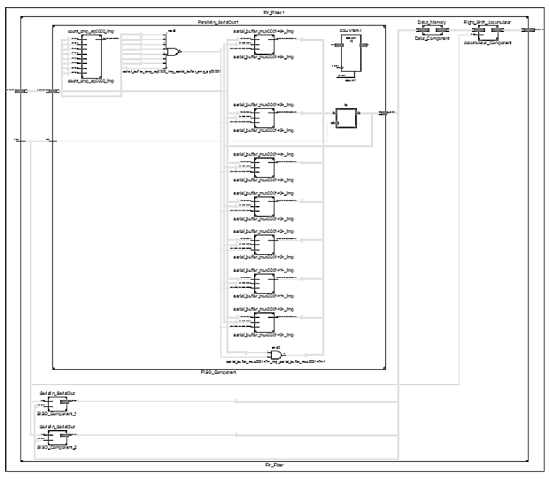
Рис. 5. Схема КИХ-фильтра с использованием распределенной арифметики.

В результате данной работы был разработан КИХ-фильтр с использованием распределенной арифметической архитектурой. Эта архитектура выделяется тем, что площадь используемого умножителя меньше обычного. Данный умножитель использует таблицы поиска, сдвиговые регистры и сумматоры с накоплением, что позволяет ему потреблять меньше ресурсов. Таким образом, распределенная арифметическая архитектура может использоваться для высокоскоростной реализации КИХ-фильтра.

Литература:

1. Сергеев В. В. Расчет параллельных КИХ-фильтров для некоторых задач обработки сигналов и изображения.
2. Сергеев В. В. Фролова Л. Г. Расчет параллельных КИХ-фильтров для некоторых задач обработки сигналов и изображения.
3. J. M. Pak, C. K. Ahn, M. T. Lim, and M. K. Song, “Horizon group shift FIR filter: Alternative nonlinear filter using finite recent measurements,” Nov. 2014
4. T. Miyata and N. Aikawa, “A design of FIR filters with variable notches considering reduction method of polynomial coefficients for real-time signal processing,” Sep. 2013.