В настоящее время в рамках машинного обучения большое внимание уделяется непараметрическим методам кластеризации, регрессии и классификации, в частности различным деревьям решений. В основе любого дерева решения лежит принцип бинарного разделения объектов на две группы исходя из байесовского принципа, нахождение объекта в одном из листов наиболее вероятно. К таким методам относятся CART, CLOPE, Random Forest.
Random Forest — один из самых популярных алгоритмов машинного обучения, придуманные Лео Брейманом и Адель Катлер ещё в прошлом веке. Алгоритм сочетает в себе две основные идеи: метод бэггинга Бреймана, и метод случайных подпространств, предложенный Tin Kam Ho. Random Forest — это множество решающих деревьев. В задаче регрессии их ответы усредняются, в задаче классификации принимается решение голосованием по большинству. Все деревья строятся независимо по следующей схеме:
1. Выбирается подвыборка обучающей выборки случайного размера, по ней строится дерево (для каждого дерева — своя подвыборка).
2. Для построения каждого расщепления в дереве просматриваем наиболее частые ветви случайных признаков (для каждого нового расщепления — свои случайные признаки).
3. Выбираем наилучший признак и расщепление по нему (по заранее заданному критерию). Дерево строится, как правило, до исчерпания выборки (пока в листьях не останутся представители только одного класса), но в современных реализациях есть параметры, которые ограничивают высоту дерева, число объектов в листьях и число объектов в подвыборке, при котором проводится расщепление.
Предположим, у нас есть некие данные на входе. Каждая колонка соответствует некоторому параметру, каждая строка соответствует некоторому элементу данных. Мы можем выбрать, случайным образом, из всего набора данных некоторое количество столбцов и строк и построить по ним дерево принятия решений (рисунок 1).
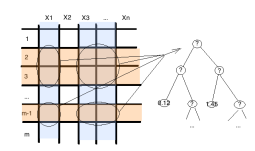
Рис. 1. Построение одного случайного дерева
Далее эту процедуру «зацикливают» в зависимости от заданного параметра нашего случайного леса, а именно повторение циклов равно количеству деревьев в лесу. Так как алгоритм построения каждого дерева достаточно прост, то исследователь практически не ограничен в количестве решающих деревьев в своем алгоритме, к тому же алгоритм построения каждого дерева достаточно быстр. К тому же, каждое дерево получается уникальным, так как для его построения выбирается каждый раз случайное подпространство.
Подведя итог всему вышесказанному, следует отметить достоинства метода:
‒ способность эффективно обрабатывать данные с большим числом признаков и классов;
‒ нечувствительность к масштабированию (и вообще к любым монотонным преобразованиям) значений признаков;
‒ одинаково хорошо обрабатываются как непрерывные, так и дискретные признаки;
‒ существуют методы построения деревьев по данным с пропущенными значениями признаков;
‒ существует методы оценивания значимости отдельных признаков в модели;
‒ благодаря воссозданию решающих правил, возрастает интерпретируемость модели и выдача рекомендаций по её использованию.
‒ робастный метод, так как робастные наблюдения уходят в отдельные листы дерева решений и не участвуют в формировании решающих правил;
‒ внутренняя оценка способности модели к обобщению;
‒ высокая параллезуемость и масштабируемость.
К недостаткам данного метода можно отнести большой размер получающихся моделей и склонность к переобучению моделей.
Оба этих недостатка решаются посредством градиентного бустинга моделей. Под термином «бустинг» от англ. «boosting» будем понимать улучшение и представляет собой процедуру последовательного построения композиции алгоритмов машинного обучения, когда каждый следующий алгоритм стремится компенсировать недостатки композиции всех предыдущих алгоритмов.
XGBoost (eXtreme Gradient Boosting Training) — один из многих открытых алгоритмов, реализующих градиентный бустинг. С точки зрения классификации бустинг деревьев решений считается одним из наиболее эффективных методов. Данный алгоритм строит модель в виде суммы деревьев:
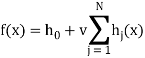 (1)
(1)
где h0 — начальное приближение, v — параметр, регулирующий скорость обучения и влияние отдельных деревьев на всю модель, hj(x) — деревья решений.
Новые слагаемые-деревья добавляются в сумму путем минимизации эмпирического риска, заданного некоторой функцией потерь:
![]() (2)
(2)
Функция:
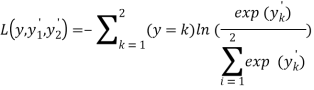 (3)
(3)
предназначена для решения задач классификации на 2 класса.
Рекомендуют использовать XGboost как наиболее продвинутую группу моделей машинного обучения. В настоящие время предиктивные модели на базе логики XGboost широко используются в финансовом и рыночном прогнозировании, маркетинге и многих других областях прикладной аналитики и машинного интеллекта.
Для реализации данных методов будем использовать среду RStudio. RStudio — свободная среда разработки программного обеспечения с открытым исходным кодом для языка программирования R, который предназначен для статистической обработки данных и работы с графикой.
Для реализации алгоритмов RandomForest [https://cran.r-project.org/web/packages/randomForest/randomForest.pdf] и XGBoost следует установить одноименные библиотеки.
Параметры для реализации метода случайного леса представлены в таблице 1.
Таблица 1
Основные параметры для настройки алгоритма RandomForest
|
Параметр |
Назначение |
|
data |
Дополнительная таблица данных, специализированного типа, содержащая информацию об объектах и их свойствах |
|
Subset |
Если для анализа следует выбрать лишь некоторые строки, то данный параметр является вектором индексов этих строк |
|
na.action |
Функция, указывающая на тип обработки пропущенных наблюдений (встроенные обработки на языке R) |
|
x, formula |
Матрица показателей или формула, указывающая объект для описания способа печати |
|
Y |
Вектор-ответ, результирующая переменная. Если данный параметр не задан, то будет запущен режим регрессии. Если параметр задан как фактор, то в режиме классификации, если же данный параметр опущен, то метод работает в неконтролируемом режиме, то есть для классификации. |
|
Xtest |
Набор данных, состояний только из предикторов для тестового набора данных |
|
Ytest |
Вектор-ответ для тестового набора данных |
|
Ntree |
Количество деревьев в лесу. Данный параметр не должен быть задан небольшим числом, так как должно гарантироваться соотношение, что каждый признак попадет в деревья решений по крайней мере несколько раз |
|
Mtry |
Количество переменных в выборке подпространства на каждом этапе ветвления. По умолчанию это число равно квадратному корню из числа всех предиктивных параметров для классификации, и числу втрое меньшему числа предиктивных параметров для регрессии |
Построим случайный лес на основе данных, по которым имеем распределение рейтингов. Ключевую переменную рейтинг зададим как некую факторную переменную, чтобы дерево решений в каждом узле получало конкретную позицию банка.
В качестве параметров модели зададим количество лесов равное 200, а также обеспечим подсчет важности факторов. Результаты построения модели представлены на рисунке 2.

Рис. 2. Параметры модели, проверка адекватности модели
Построенная модель на 84,24 % адекватно описывает текущие данные, а значит правомерным является использование ее для прогноза. На рисунке 3 представлен график оценки значимости факторов на итоговое ранжирование.
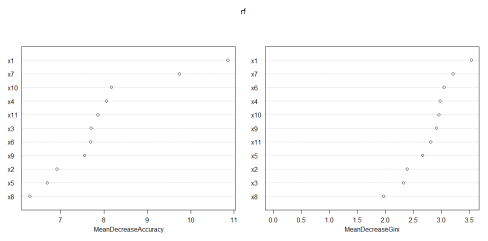
Рис. 3. Оценка значимости факторов на ранжирование банков
Как можем заметить, наиболее весомым признаками оказались «Средства акционеров (участников) (тыс.руб.)» и «процентная ставка по кредиту (%)», что не противоречит ранее полученным результатам.
Построим прогноз на основе полученных деревьев решений для банков, для которых отсутствовала начальная ранжировка, результаты представлены на рисунке 4.
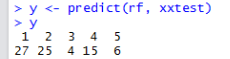
Рис. 4. Результаты прогнозирования для ранжировки банков
Согласно полученным данным ОАО «Нико-Банк» следует отнести к 27 позиции, а ЗАО «РКБ», ОАО «Россельхозбанк», ПАО «Нота-Банк», ПАО «Росбанк» к 25, 4, 15 и 6 соответственно.
Преимущество деревьев решений состоит в том, что можно посмотреть бинарные правила, согласно которым определяется отнесения к какому-либо классу.
Исходя из того, что нами было задано число случайных деревьев равное 200, мы получили порядка 1000 решающих правил. Даже произведя отбор по частоте попадания объектов в конечные листы деревьев решений, все равно количество решающих правил для рассмотрения остается достаточно велико. Следовательно, мы столкнулись с недостатков модели, а именно с ее громоздкостью. Для того, чтобы решить возникшую проблему воспользуемся градиентным бустингом. Результаты оценки ошибки представлены на рисунке 5:
![]()
Рис. 5. Ошибка модели RandomForest после использования градиентного бустинга
Таким образом, адекватность построенной модели после применения XGBoosting значительно возросла.
Литература:
- Дружнов, П.Н., Золотых, Н.Ю., Половинкин, А. Н. Программная реализация алгоритма градиентного бустинга деревьев решений / П. Н. Дружнов, Н. Ю. Зотолых, А.Ню Половинкин // Вестник Нижегородского университета им. Н. И. Лобачевского, 2011.-№ 1.-С.193–200.
- Дружнов, П.Н., Золотых, Н.Ю., Половинкин, А. Н. Реализация параллельного алгоритма предсказания в методе градиентного бустинга деревьев решений / П. Н. Дружнов, Н. Ю. Зотолых, А. Н. Половинкин // Вестник Южно-Уральского государственного университета. Серия: Математическое моделирование и программирование, 2011.-№ 37 (254).-С.82–89.
- Дружнов, П. Н. Параллельная реализация алгоритма градиентного бустинга деревьев решений / П. Н. Дружнов // Вычислительные методы и программирование: новые вычислительные технологии, 2013.-№ 2 (28).-С.109–114.

